Question Number 149795 by mathdanisur last updated on 07/Aug/21

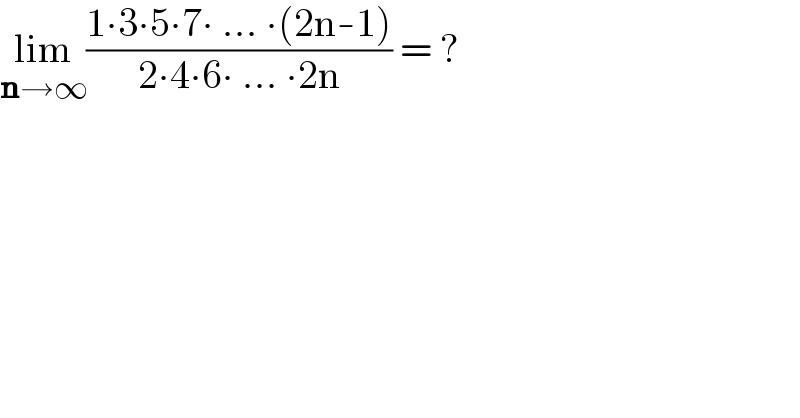
lim_(n→∞) ((1∙3∙5∙7∙ ... ∙(2n-1))/(2∙4∙6∙ ... ∙2n)) = ?

Answered by mathmax by abdo last updated on 07/Aug/21

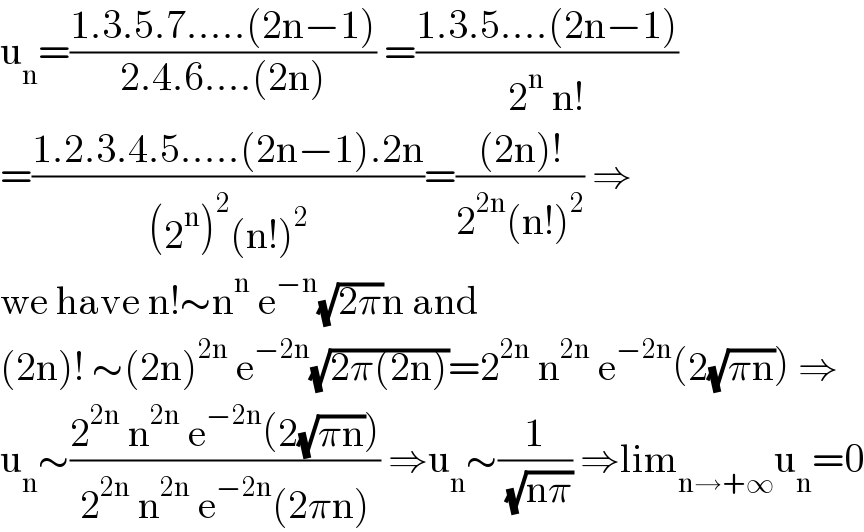
u_n =((1.3.5.7.....(2n−1))/(2.4.6....(2n))) =((1.3.5....(2n−1))/(2^n n!)) =((1.2.3.4.5.....(2n−1).2n)/((2^n )^2 (n!)^2 ))=(((2n)!)/(2^(2n) (n!)^2 )) ⇒ we have n!∼n^n e^(−n) (√(2π))n and (2n)! ∼(2n)^(2n) e^(−2n) (√(2π(2n)))=2^(2n) n^(2n) e^(−2n) (2(√(πn))) ⇒ u_n ∼((2^(2n) n^(2n) e^(−2n) (2(√(πn))))/(2^(2n) n^(2n) e^(−2n) (2πn))) ⇒u_n ∼(1/( (√(nπ)))) ⇒lim_(n→+∞) u_n =0

Commented bymathdanisur last updated on 07/Aug/21

Thank you Ser