
Question Number 149805 by mnjuly1970 last updated on 07/Aug/21
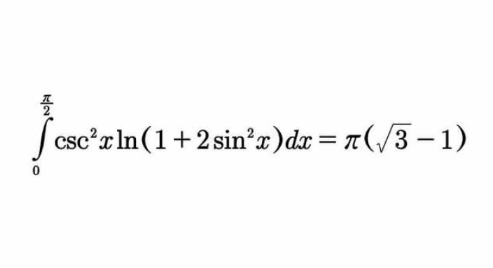
Answered by Ar Brandon last updated on 07/Aug/21
![I=∫_0 ^(π/2) csc^2 xln(1+2sin^2 x)dx { ((u(x)=ln(1+2sin^2 x))),((v′(x)=csc^2 x)) :}⇒ { ((u′(x)=((2sin2x)/(1+2sin^2 x)))),((v(x)=−cotx)) :} I=[−cotx∙ln(1+2sin^2 x)]_0 ^(π/2) +4∫_0 ^(π/2) ((sinxcos^2 x)/(sinx+2sin^3 x))dx =−4∫_0 ^(π/2) ((sin^2 x−1)/(2sin^2 x+1))dx=−2∫_0 ^(π/2) (1−(3/(2sin^2 x+1)))dx =−π+6∫_0 ^(π/2) ((sec^2 x)/(2tan^2 x+sec^2 x))dx=−π+6∫_0 ^(π/2) ((d(tanx))/(3tan^2 x+1)) =−π+2∙(√3)[arctan((√3)tanx)]_0 ^(π/2) =π((√3)−1)](Q149806.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{csc}^{\mathrm{2}} {x}\mathrm{ln}\left(\mathrm{1}+\mathrm{2sin}^{\mathrm{2}} {x}\right){dx} \\ $$$$\begin{cases}{{u}\left({x}\right)=\mathrm{ln}\left(\mathrm{1}+\mathrm{2sin}^{\mathrm{2}} {x}\right)}\\{{v}'\left({x}\right)=\mathrm{csc}^{\mathrm{2}} {x}}\end{cases}\Rightarrow\begin{cases}{{u}'\left({x}\right)=\frac{\mathrm{2sin2}{x}}{\mathrm{1}+\mathrm{2sin}^{\mathrm{2}} {x}}}\\{{v}\left({x}\right)=−\mathrm{cot}{x}}\end{cases} \\ $$$${I}=\left[−\mathrm{cot}{x}\centerdot\mathrm{ln}\left(\mathrm{1}+\mathrm{2sin}^{\mathrm{2}} {x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}{x}\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{sin}{x}+\mathrm{2sin}^{\mathrm{3}} {x}}{dx} \\ $$$$\:\:=−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{2sin}^{\mathrm{2}} {x}+\mathrm{1}}{dx}=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2sin}^{\mathrm{2}} {x}+\mathrm{1}}\right){dx} \\ $$$$\:\:=−\pi+\mathrm{6}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} {x}}{\mathrm{2tan}^{\mathrm{2}} {x}+\mathrm{sec}^{\mathrm{2}} {x}}{dx}=−\pi+\mathrm{6}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left(\mathrm{tan}{x}\right)}{\mathrm{3tan}^{\mathrm{2}} {x}+\mathrm{1}} \\ $$$$\:\:=−\pi+\mathrm{2}\centerdot\sqrt{\mathrm{3}}\left[\mathrm{arctan}\left(\sqrt{\mathrm{3}}\mathrm{tan}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\pi\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$
Commented by mnjuly1970 last updated on 07/Aug/21
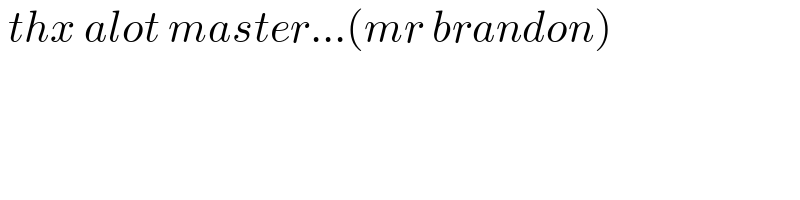
$$\:{thx}\:{alot}\:{master}...\left({mr}\:{brandon}\right) \\ $$
Commented by Ar Brandon last updated on 07/Aug/21

$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome}\:! \\ $$$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{celebrate}\:\mathrm{your}\:\mathrm{birthday},\:\mathrm{Sir}\:? \\ $$$$\mathrm{I}\:\mathrm{guess}\:\mathrm{july}\:\mathrm{1970}\:\mathrm{represents}\:\mathrm{your}\:\mathrm{month}\:\mathrm{and} \\ $$$$\mathrm{year}\:\mathrm{of}\:\mathrm{birth}. \\ $$😄😅
