Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 149853 by 0731619 last updated on 07/Aug/21

Answered by mindispower last updated on 08/Aug/21

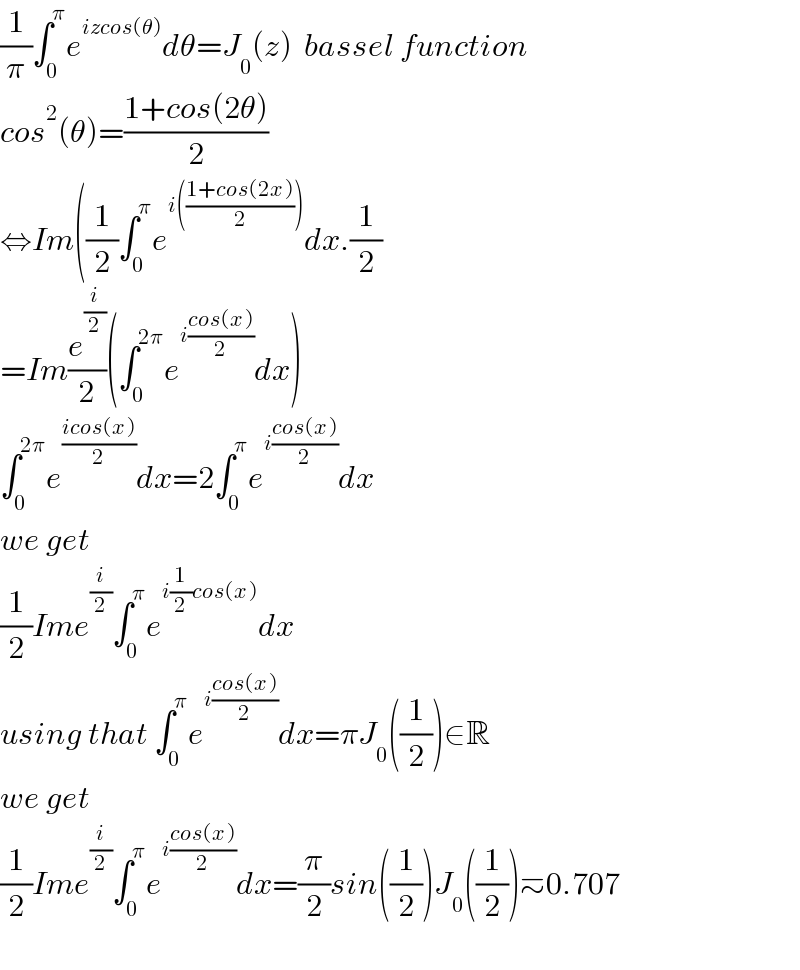
(1/π)∫_0 ^π e^(izcos(θ)) dθ=J_0 (z) bassel function cos^2 (θ)=((1+cos(2θ))/2) ⇔Im((1/2)∫_0 ^π e^(i(((1+cos(2x))/2))) dx.(1/2) =Im(e^(i/2) /2)(∫_0 ^(2π) e^(i((cos(x))/2)) dx) ∫_0 ^(2π) e^((icos(x))/2) dx=2∫_0 ^π e^(i((cos(x))/2)) dx we get (1/2)Ime^(i/2) ∫_0 ^π e^(i(1/2)cos(x)) dx using that ∫_0 ^π e^(i((cos(x))/2)) dx=πJ_0 ((1/2))∈R we get (1/2)Ime^(i/2) ∫_0 ^π e^(i((cos(x))/2)) dx=(π/2)sin((1/2))J_0 ((1/2))≃0.707

$$\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\pi} {e}^{{izcos}\left(\theta\right)} {d}\theta={J}_{\mathrm{0}} \left({z}\right)\:\:{bassel}\:{function} \\ $$$${cos}^{\mathrm{2}} \left(\theta\right)=\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}} \\ $$$$\Leftrightarrow{Im}\left(\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} {e}^{{i}\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)} {dx}.\frac{\mathrm{1}}{\mathrm{2}}\right. \\ $$$$={Im}\frac{{e}^{\frac{{i}}{\mathrm{2}}} }{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{{i}\frac{{cos}\left({x}\right)}{\mathrm{2}}} {dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {e}^{\frac{{icos}\left({x}\right)}{\mathrm{2}}} {dx}=\mathrm{2}\int_{\mathrm{0}} ^{\pi} {e}^{{i}\frac{{cos}\left({x}\right)}{\mathrm{2}}} {dx} \\ $$$${we}\:{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{Ime}^{\frac{{i}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\pi} {e}^{{i}\frac{\mathrm{1}}{\mathrm{2}}{cos}\left({x}\right)} {dx} \\ $$$${using}\:{that}\:\int_{\mathrm{0}} ^{\pi} {e}^{{i}\frac{{cos}\left({x}\right)}{\mathrm{2}}} {dx}=\pi{J}_{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\in\mathbb{R} \\ $$$${we}\:{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{Ime}^{\frac{{i}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\pi} {e}^{{i}\frac{{cos}\left({x}\right)}{\mathrm{2}}} {dx}=\frac{\pi}{\mathrm{2}}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){J}_{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\simeq\mathrm{0}.\mathrm{707} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com