Question Number 149885 by puissant last updated on 08/Aug/21

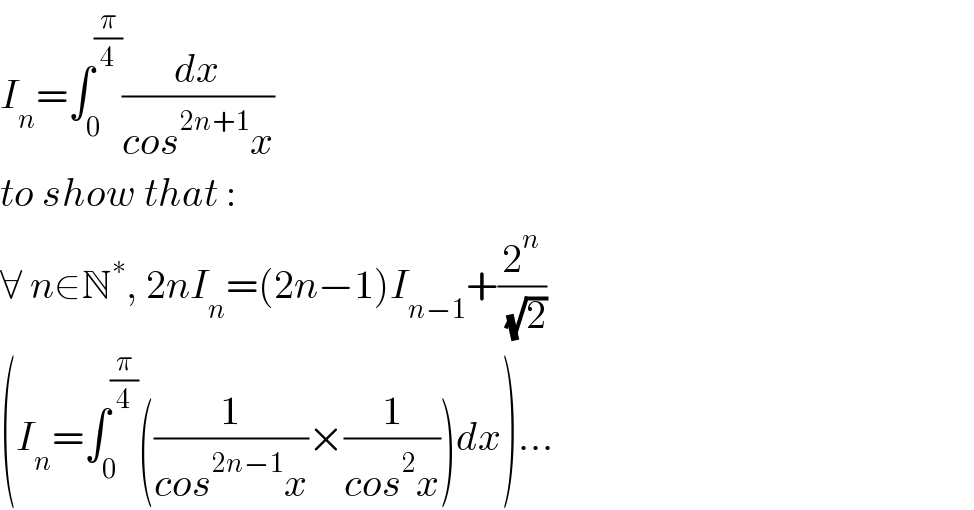
I_n =∫_0 ^(π/4) (dx/(cos^(2n+1) x)) to show that : ∀ n∈N^∗ , 2nI_n =(2n−1)I_(n−1) +(2^n /( (√2))) (I_n =∫_0 ^(π/4) ((1/(cos^(2n−1) x))×(1/(cos^2 x)))dx)...

Answered by Ar Brandon last updated on 08/Aug/21

I_n =∫_0 ^(π/4) (dx/(cos^(2n+1) x))=∫_0 ^(π/4) ((sec^2 x)/(cos^(2n−1) x))dx =[((tanx)/(cos^(2n−1) x))]_0 ^(π/4) −(2n−1)∫_0 ^(π/4) ((sin^2 x)/(cos^(2n+1) x))dx

Commented byAr Brandon last updated on 08/Aug/21

sin^2 x=1−cos^2 x You may proceed...

Commented bypuissant last updated on 27/Aug/21

oui en posant sin^2 (x)=1−cos^2 (x) ca passe j′ai reussi a ecraser ca merci brooo...

Commented byAr Brandon last updated on 08/Aug/21

D′accord, ravi ! J′e^� tais presse^�

Commented bypuissant last updated on 08/Aug/21

confiance..