Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 150721 by cesarL last updated on 14/Aug/21

calculate the convergence interval of the serie Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!))

$${calculate}\:{the}\:{convergence}\:{interval}\:{of}\:{the} \\ $$$${serie} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{{n}!} \\ $$

Answered by ArielVyny last updated on 15/Aug/21

Δ=]a−R;a+R[ (convergence inrerval) a=0 R=lim((((−1)^(n+1) )/((n+1)!))×((n!)/((−1)^n )))=lim(−(1/(n+1)))=0 (d′alembert) Δ={0}

$$\left.\Delta=\right]{a}−{R};{a}+{R}\left[\:\left({convergence}\:{inrerval}\right)\:\:\:{a}=\mathrm{0}\:\:{R}={lim}\left(\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}×\frac{{n}!}{\left(−\mathrm{1}\right)^{{n}} }\right)={lim}\left(−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)=\mathrm{0}\:\left({d}'{alembert}\right)\right. \\ $$$$\Delta=\left\{\mathrm{0}\right\} \\ $$

Answered by mathmax by abdo last updated on 17/Aug/21

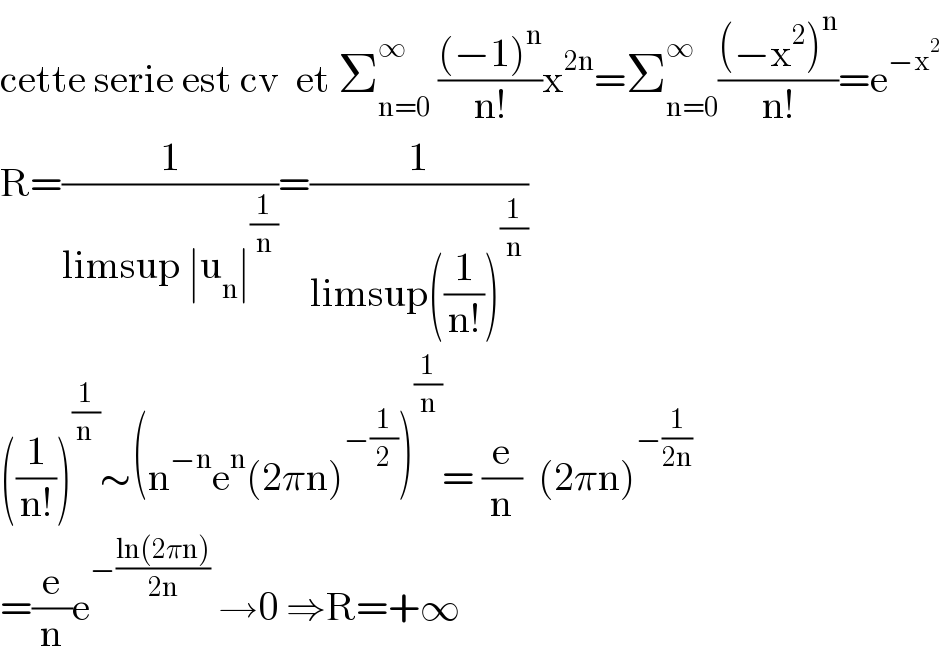
cette serie est cv et Σ_(n=0) ^∞ (((−1)^n )/(n!))x^(2n) =Σ_(n=0) ^∞ (((−x^2 )^n )/(n!))=e^(−x^2 ) R=(1/(limsup ∣u_n ∣^(1/n) ))=(1/(limsup((1/(n!)))^(1/n) )) ((1/(n!)))^(1/(n )) ∼(n^(−n) e^n (2πn)^(−(1/2)) )^(1/n) = (e/n) (2πn)^(−(1/(2n))) =(e/n)e^(−((ln(2πn))/(2n))) →0 ⇒R=+∞

$$\mathrm{cette}\:\mathrm{serie}\:\mathrm{est}\:\mathrm{cv}\:\:\mathrm{et}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}!}\mathrm{x}^{\mathrm{2n}} =\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }{\mathrm{n}!}=\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{R}=\frac{\mathrm{1}}{\mathrm{limsup}\:\mid\mathrm{u}_{\mathrm{n}} \mid^{\frac{\mathrm{1}}{\mathrm{n}}} }=\frac{\mathrm{1}}{\mathrm{limsup}\left(\frac{\mathrm{1}}{\mathrm{n}!}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} } \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{n}!}\right)^{\frac{\mathrm{1}}{\mathrm{n}\:}} \sim\left(\mathrm{n}^{−\mathrm{n}} \mathrm{e}^{\mathrm{n}} \left(\mathrm{2}\pi\mathrm{n}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{n}}} =\:\frac{\mathrm{e}}{\mathrm{n}}\:\:\left(\mathrm{2}\pi\mathrm{n}\right)^{−\frac{\mathrm{1}}{\mathrm{2n}}} \\ $$$$=\frac{\mathrm{e}}{\mathrm{n}}\mathrm{e}^{−\frac{\mathrm{ln}\left(\mathrm{2}\pi\mathrm{n}\right)}{\mathrm{2n}}} \:\rightarrow\mathrm{0}\:\Rightarrow\mathrm{R}=+\infty \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com