Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 152241 by ZiYangLee last updated on 26/Aug/21

Answered by Olaf_Thorendsen last updated on 26/Aug/21

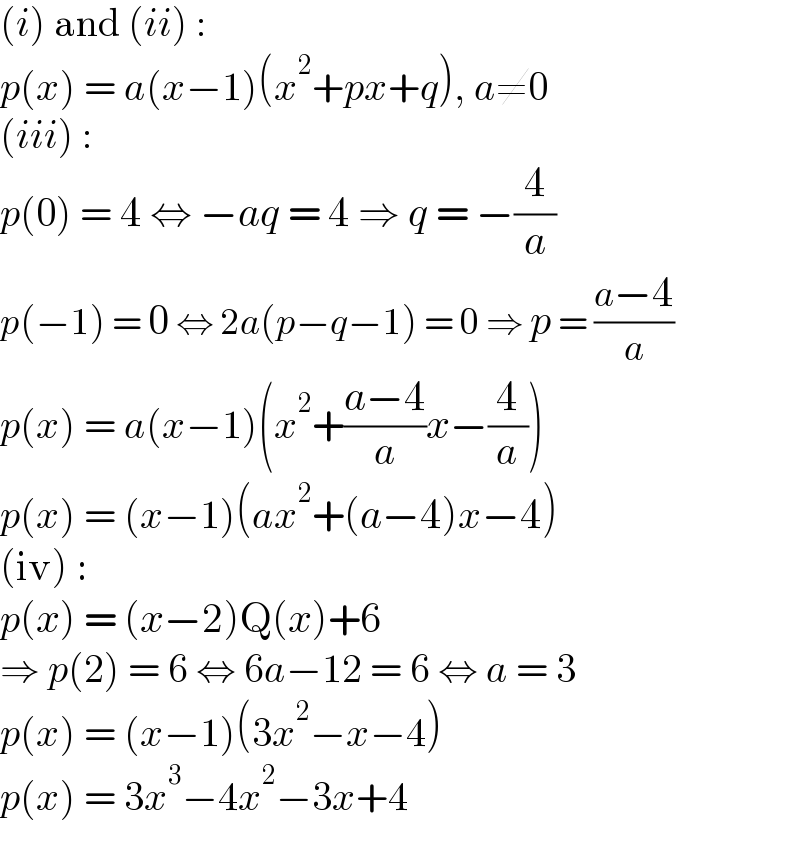
(i) and (ii) : p(x) = a(x−1)(x^2 +px+q), a≠0 (iii) : p(0) = 4 ⇔ −aq = 4 ⇒ q = −(4/a) p(−1) = 0 ⇔ 2a(p−q−1) = 0 ⇒ p = ((a−4)/a) p(x) = a(x−1)(x^2 +((a−4)/a)x−(4/a)) p(x) = (x−1)(ax^2 +(a−4)x−4) (iv) : p(x) = (x−2)Q(x)+6 ⇒ p(2) = 6 ⇔ 6a−12 = 6 ⇔ a = 3 p(x) = (x−1)(3x^2 −x−4) p(x) = 3x^3 −4x^2 −3x+4

$$\left({i}\right)\:\mathrm{and}\:\left({ii}\right)\:: \\ $$$${p}\left({x}\right)\:=\:{a}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{px}+{q}\right),\:{a}\neq\mathrm{0} \\ $$$$\left({iii}\right)\:: \\ $$$${p}\left(\mathrm{0}\right)\:=\:\mathrm{4}\:\Leftrightarrow\:−{aq}\:=\:\mathrm{4}\:\Rightarrow\:{q}\:=\:−\frac{\mathrm{4}}{{a}} \\ $$$${p}\left(−\mathrm{1}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:\mathrm{2}{a}\left({p}−{q}−\mathrm{1}\right)\:=\:\mathrm{0}\:\Rightarrow\:{p}\:=\:\frac{{a}−\mathrm{4}}{{a}} \\ $$$${p}\left({x}\right)\:=\:{a}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\frac{{a}−\mathrm{4}}{{a}}{x}−\frac{\mathrm{4}}{{a}}\right) \\ $$$${p}\left({x}\right)\:=\:\left({x}−\mathrm{1}\right)\left({ax}^{\mathrm{2}} +\left({a}−\mathrm{4}\right){x}−\mathrm{4}\right) \\ $$$$\left(\mathrm{iv}\right)\:: \\ $$$${p}\left({x}\right)\:=\:\left({x}−\mathrm{2}\right)\mathrm{Q}\left({x}\right)+\mathrm{6} \\ $$$$\Rightarrow\:{p}\left(\mathrm{2}\right)\:=\:\mathrm{6}\:\Leftrightarrow\:\mathrm{6}{a}−\mathrm{12}\:=\:\mathrm{6}\:\Leftrightarrow\:{a}\:=\:\mathrm{3} \\ $$$${p}\left({x}\right)\:=\:\left({x}−\mathrm{1}\right)\left(\mathrm{3}{x}^{\mathrm{2}} −{x}−\mathrm{4}\right) \\ $$$${p}\left({x}\right)\:=\:\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4} \\ $$

Answered by john_santu last updated on 27/Aug/21

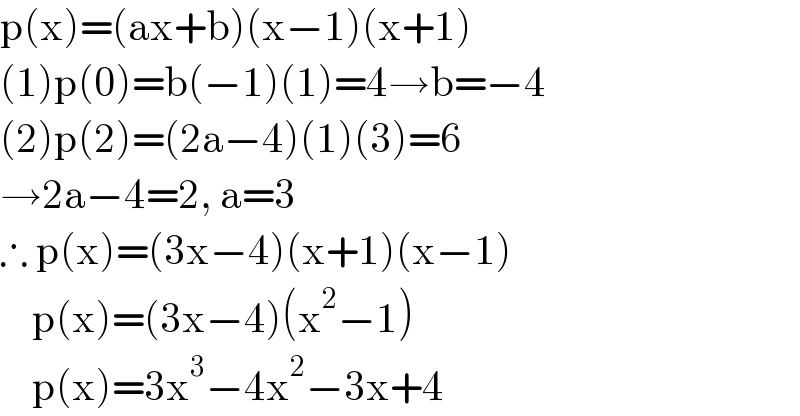
p(x)=(ax+b)(x−1)(x+1) (1)p(0)=b(−1)(1)=4→b=−4 (2)p(2)=(2a−4)(1)(3)=6 →2a−4=2, a=3 ∴ p(x)=(3x−4)(x+1)(x−1) p(x)=(3x−4)(x^2 −1) p(x)=3x^3 −4x^2 −3x+4

$$\mathrm{p}\left(\mathrm{x}\right)=\left(\mathrm{ax}+\mathrm{b}\right)\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right) \\ $$$$\left(\mathrm{1}\right)\mathrm{p}\left(\mathrm{0}\right)=\mathrm{b}\left(−\mathrm{1}\right)\left(\mathrm{1}\right)=\mathrm{4}\rightarrow\mathrm{b}=−\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\mathrm{p}\left(\mathrm{2}\right)=\left(\mathrm{2a}−\mathrm{4}\right)\left(\mathrm{1}\right)\left(\mathrm{3}\right)=\mathrm{6} \\ $$$$\rightarrow\mathrm{2a}−\mathrm{4}=\mathrm{2},\:\mathrm{a}=\mathrm{3} \\ $$$$\therefore\:\mathrm{p}\left(\mathrm{x}\right)=\left(\mathrm{3x}−\mathrm{4}\right)\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{1}\right) \\ $$$$\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)=\left(\mathrm{3x}−\mathrm{4}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)=\mathrm{3x}^{\mathrm{3}} −\mathrm{4x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{4} \\ $$

Answered by Rasheed.Sindhi last updated on 27/Aug/21

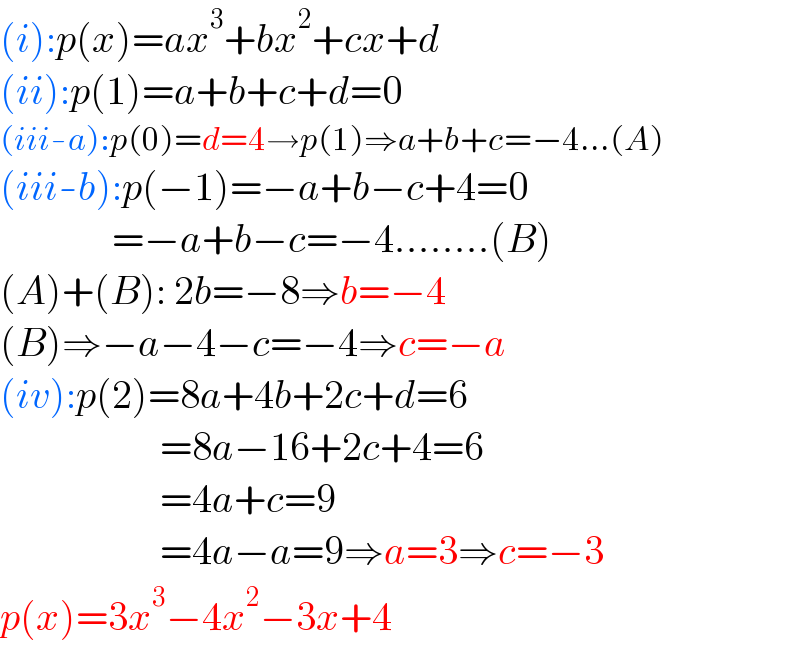
(i):p(x)=ax^3 +bx^2 +cx+d (ii):p(1)=a+b+c+d=0 (iii-a):p(0)=d=4→p(1)⇒a+b+c=−4...(A) (iii-b):p(−1)=−a+b−c+4=0 =−a+b−c=−4........(B) (A)+(B): 2b=−8⇒b=−4 (B)⇒−a−4−c=−4⇒c=−a (iv):p(2)=8a+4b+2c+d=6 =8a−16+2c+4=6 =4a+c=9 =4a−a=9⇒a=3⇒c=−3 p(x)=3x^3 −4x^2 −3x+4

$$\left({i}\right):{p}\left({x}\right)={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$$\left({ii}\right):{p}\left(\mathrm{1}\right)={a}+{b}+{c}+{d}=\mathrm{0} \\ $$$$\left({iii}-{a}\right):{p}\left(\mathrm{0}\right)={d}=\mathrm{4}\rightarrow{p}\left(\mathrm{1}\right)\Rightarrow{a}+{b}+{c}=−\mathrm{4}...\left({A}\right) \\ $$$$\left({iii}-{b}\right):{p}\left(−\mathrm{1}\right)=−{a}+{b}−{c}+\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−{a}+{b}−{c}=−\mathrm{4}........\left({B}\right) \\ $$$$\left({A}\right)+\left({B}\right):\:\mathrm{2}{b}=−\mathrm{8}\Rightarrow{b}=−\mathrm{4} \\ $$$$\left({B}\right)\Rightarrow−{a}−\mathrm{4}−{c}=−\mathrm{4}\Rightarrow{c}=−{a} \\ $$$$\left({iv}\right):{p}\left(\mathrm{2}\right)=\mathrm{8}{a}+\mathrm{4}{b}+\mathrm{2}{c}+{d}=\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{8}{a}−\mathrm{16}+\mathrm{2}{c}+\mathrm{4}=\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}{a}+{c}=\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}{a}−{a}=\mathrm{9}\Rightarrow{a}=\mathrm{3}\Rightarrow{c}=−\mathrm{3} \\ $$$${p}\left({x}\right)=\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4} \\ $$

Answered by Rasheed.Sindhi last updated on 27/Aug/21

≪By Synthetic Division≫ (i): ax^3 +bx^2 +cx+d (ii): x−1 is factor of p(x) determinant (((1)),a,b,c,d),(,,a,(a+b),(a+b+c)),(,a,(a+b),(a+b+c),(a+b+c+d=0))) (iiia):p(0)=4 determinant (((0)),a,b,c,d),(,,0,0,0),(,a,b,c,(d=4))) (iiib):p(−1)=0 determinant (((−1)),a,b,c,d),(,,(−a),(a−b),(−a+b−c)),(,a,(−a+b),(a−b+c),(−a+b−c+d=0))) (iv):p(2)=6 determinant (((2)),a,b,c,d),(,,(2a),(4a+2b),(8a+4b+2c)),(,a,(2a+b),(4a+2b+c),(8a+4b+2c+d=6))) { ((a+b+c+d=0)),((d=4)),((−a+b−c+d=0)),((8a+4b+2c+d=6)) :}⇒ { ((a+b+c+4=0...(1))),((−a+b−c+4=0...(2))),((8a+4b+2c+4=6...(3))) :} (1)+(2):2b+8=0⇒b=−4 (2)⇒a+c=0⇒c=−a (3)⇒8a−16−2a+4=6⇒a=3⇒c=−3 p(x)=3x^3 −4x^2 −3x+4

$$\:\:\:\:\:\:\:\:\ll\mathcal{B}{y}\:\mathcal{S}{ynthetic}\:\mathcal{D}{ivision}\gg \\ $$$$\left({i}\right):\:{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$$\left({ii}\right):\:{x}−\mathrm{1}\:{is}\:{factor}\:{of}\:{p}\left({x}\right) \\ $$$$\:\:\:\begin{array}{|c|c|c|}{\left.\mathrm{1}\right)}&\hline{{a}}&\hline{{b}}&\hline{{c}}&\hline{{d}}\\{}&\hline{}&\hline{{a}}&\hline{{a}+{b}}&\hline{{a}+{b}+{c}}\\{}&\hline{{a}}&\hline{{a}+{b}}&\hline{{a}+{b}+{c}}&\hline{{a}+{b}+{c}+{d}=\mathrm{0}}\\\hline\end{array}\: \\ $$$$\left({iiia}\right):{p}\left(\mathrm{0}\right)=\mathrm{4} \\ $$$$\:\:\:\begin{array}{|c|c|c|}{\left.\mathrm{0}\right)}&\hline{{a}}&\hline{{b}}&\hline{{c}}&\hline{{d}}\\{}&\hline{}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}\\{}&\hline{{a}}&\hline{{b}}&\hline{{c}}&\hline{{d}=\mathrm{4}}\\\hline\end{array}\: \\ $$$$\left({iiib}\right):{p}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\begin{array}{|c|c|c|}{\left.−\mathrm{1}\right)}&\hline{{a}}&\hline{{b}}&\hline{{c}}&\hline{{d}}\\{}&\hline{}&\hline{−{a}}&\hline{{a}−{b}}&\hline{−{a}+{b}−{c}}\\{}&\hline{{a}}&\hline{−{a}+{b}}&\hline{{a}−{b}+{c}}&\hline{−{a}+{b}−{c}+{d}=\mathrm{0}}\\\hline\end{array} \\ $$$$\left({iv}\right):{p}\left(\mathrm{2}\right)=\mathrm{6}\: \\ $$$$\begin{array}{|c|c|c|}{\left.\mathrm{2}\right)}&\hline{{a}}&\hline{{b}}&\hline{{c}}&\hline{{d}}\\{}&\hline{}&\hline{\mathrm{2}{a}}&\hline{\mathrm{4}{a}+\mathrm{2}{b}}&\hline{\mathrm{8}{a}+\mathrm{4}{b}+\mathrm{2}{c}}\\{}&\hline{{a}}&\hline{\mathrm{2}{a}+{b}}&\hline{\mathrm{4}{a}+\mathrm{2}{b}+{c}}&\hline{\mathrm{8}{a}+\mathrm{4}{b}+\mathrm{2}{c}+{d}=\mathrm{6}}\\\hline\end{array}\: \\ $$$$\begin{cases}{{a}+{b}+{c}+{d}=\mathrm{0}}\\{{d}=\mathrm{4}}\\{−{a}+{b}−{c}+{d}=\mathrm{0}}\\{\mathrm{8}{a}+\mathrm{4}{b}+\mathrm{2}{c}+{d}=\mathrm{6}}\end{cases}\Rightarrow\begin{cases}{{a}+{b}+{c}+\mathrm{4}=\mathrm{0}...\left(\mathrm{1}\right)}\\{−{a}+{b}−{c}+\mathrm{4}=\mathrm{0}...\left(\mathrm{2}\right)}\\{\mathrm{8}{a}+\mathrm{4}{b}+\mathrm{2}{c}+\mathrm{4}=\mathrm{6}...\left(\mathrm{3}\right)}\end{cases} \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right):\mathrm{2}{b}+\mathrm{8}=\mathrm{0}\Rightarrow{b}=−\mathrm{4} \\ $$$$\left(\mathrm{2}\right)\Rightarrow{a}+{c}=\mathrm{0}\Rightarrow{c}=−{a} \\ $$$$\left(\mathrm{3}\right)\Rightarrow\mathrm{8}{a}−\mathrm{16}−\mathrm{2}{a}+\mathrm{4}=\mathrm{6}\Rightarrow{a}=\mathrm{3}\Rightarrow{c}=−\mathrm{3} \\ $$$${p}\left({x}\right)=\mathrm{3}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{4} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com