
Question Number 154647 by mathdanisur last updated on 20/Sep/21
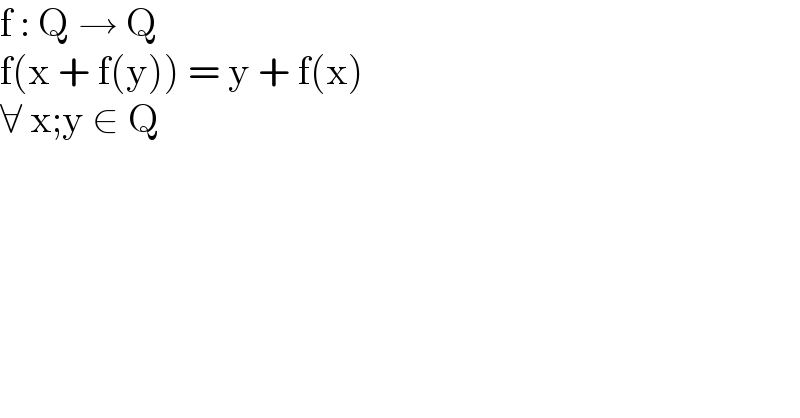
$$\mathrm{f}\::\:\mathrm{Q}\:\rightarrow\:\mathrm{Q} \\ $$$$\mathrm{f}\left(\mathrm{x}\:+\:\mathrm{f}\left(\mathrm{y}\right)\right)\:=\:\mathrm{y}\:+\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\forall\:\mathrm{x};\mathrm{y}\:\in\:\mathrm{Q} \\ $$
Answered by TheHoneyCat last updated on 20/Sep/21
![I demote by f^n : f○...○f n times I wont precise it, but when a value (x,y,z...) is not defined it means it can be any element of Q let I be the identity function I am assuming that Q here stands for Q the set of rationnals but note that this proof works on any group were −2,−1,0,1,2 are all distinct I am also assuming that the question is: “Find all f such that [your proprety]” evaluating for x=0 we get: f^2 (y)=y+f(0) applying f over that equality we get: f^3 (y)=f(y+f(0))=0+f(y) hence: f^3 =f (1) f(x+f(y))=y+f(x) f(−f(y)+f(y))=y+f(f(y)) i.e. f(0)−y=f^2 (y) so f^3 (y)=f(−y+f(0))=f(−y) i.e. f^3 =f○(−I) hence f=f○(−I) (2) y+f(x)=y+f(−x)=f(−x+f(y))=f(x+f(y)) f(0)=f(2f(y)) f(2f(y))=y+f(y)=f(0) so f^2 =f (3) f(x+f(y))=y+f(x) f^2 (y)=f(y)+f(0) so f(0)=0 so f(y)=−y but then y!=0 ⇒ f(−y)!=f(y) this contradicts (2) therefore there is no such function_■](Q154692.png)
$$\mathrm{I}\:\mathrm{demote}\:\mathrm{by}\:{f}^{{n}} \::\:{f}\circ...\circ{f}\:{n}\:\mathrm{times} \\ $$$$\mathrm{I}\:\mathrm{wont}\:\mathrm{precise}\:\mathrm{it},\:\mathrm{but}\:\mathrm{when}\:\mathrm{a}\:\mathrm{value}\:\left({x},{y},{z}...\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{it}\:\mathrm{means}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{any}\:\mathrm{element}\:\mathrm{of}\:\mathbb{Q} \\ $$$$\mathrm{let}\:\mathbb{I}\:\mathrm{be}\:\mathrm{the}\:\mathrm{identity}\:\mathrm{function} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{assuming}\:\mathrm{that}\:\mathrm{Q}\:\mathrm{here}\:\mathrm{stands}\:\mathrm{for}\:\mathbb{Q}\:\mathrm{the}\:\mathrm{set}\:\mathrm{of}\:\mathrm{rationnals} \\ $$$$\mathrm{but}\:\mathrm{note}\:\mathrm{that}\:\mathrm{this}\:\mathrm{proof}\:\mathrm{works}\:\mathrm{on}\:\mathrm{any}\:\mathrm{group}\:\mathrm{were}\:−\mathrm{2},−\mathrm{1},\mathrm{0},\mathrm{1},\mathrm{2}\:\mathrm{are}\:\mathrm{all}\:\mathrm{distinct} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{also}\:\mathrm{assuming}\:\mathrm{that}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}: \\ $$$$``\mathrm{Find}\:\mathrm{all}\:{f}\:\mathrm{such}\:\mathrm{that}\:\left[{your}\:{proprety}\right]'' \\ $$$$ \\ $$$$\mathrm{evaluating}\:\mathrm{for}\:{x}=\mathrm{0}\:\mathrm{we}\:\mathrm{get}: \\ $$$${f}^{\mathrm{2}} \left({y}\right)={y}+{f}\left(\mathrm{0}\right) \\ $$$$\mathrm{applying}\:{f}\:\mathrm{over}\:\mathrm{that}\:\mathrm{equality}\:\mathrm{we}\:\mathrm{get}: \\ $$$${f}^{\mathrm{3}} \left({y}\right)={f}\left({y}+{f}\left(\mathrm{0}\right)\right)=\mathrm{0}+{f}\left({y}\right) \\ $$$$\mathrm{hence}:\:{f}^{\mathrm{3}} ={f}\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$${f}\left({x}+{f}\left({y}\right)\right)={y}+{f}\left({x}\right) \\ $$$${f}\left(−{f}\left({y}\right)+{f}\left({y}\right)\right)={y}+{f}\left({f}\left({y}\right)\right) \\ $$$$\mathrm{i}.\mathrm{e}.\:{f}\left(\mathrm{0}\right)−{y}={f}^{\mathrm{2}} \left({y}\right) \\ $$$$\mathrm{so}\:{f}^{\mathrm{3}} \left({y}\right)={f}\left(−{y}+{f}\left(\mathrm{0}\right)\right)={f}\left(−{y}\right) \\ $$$$\mathrm{i}.\mathrm{e}.\:{f}^{\mathrm{3}} ={f}\circ\left(−\mathbb{I}\right) \\ $$$$\mathrm{hence}\:{f}={f}\circ\left(−\mathbb{I}\right)\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$${y}+{f}\left({x}\right)={y}+{f}\left(−{x}\right)={f}\left(−{x}+{f}\left({y}\right)\right)={f}\left({x}+{f}\left({y}\right)\right) \\ $$$${f}\left(\mathrm{0}\right)={f}\left(\mathrm{2}{f}\left({y}\right)\right) \\ $$$${f}\left(\mathrm{2}{f}\left({y}\right)\right)={y}+{f}\left({y}\right)={f}\left(\mathrm{0}\right) \\ $$$$\mathrm{so}\:{f}^{\mathrm{2}} ={f}\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$${f}\left({x}+{f}\left({y}\right)\right)={y}+{f}\left({x}\right) \\ $$$${f}^{\mathrm{2}} \left({y}\right)={f}\left({y}\right)+{f}\left(\mathrm{0}\right)\:{so}\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{so}\:{f}\left({y}\right)=−{y} \\ $$$$\mathrm{but}\:\mathrm{then}\:{y}!=\mathrm{0}\:\Rightarrow\:{f}\left(−{y}\right)!={f}\left({y}\right) \\ $$$$\mathrm{this}\:\mathrm{contradicts}\:\left(\mathrm{2}\right)\: \\ $$$$ \\ $$$$\mathrm{therefore}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{such}\:\mathrm{function}_{\blacksquare} \\ $$$$\: \\ $$
Commented by mathdanisur last updated on 20/Sep/21
$$\mathrm{Perfect}\:\mathrm{solution}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thanks} \\ $$
