
Question Number 155477 by alcohol last updated on 01/Oct/21

Answered by puissant last updated on 01/Oct/21
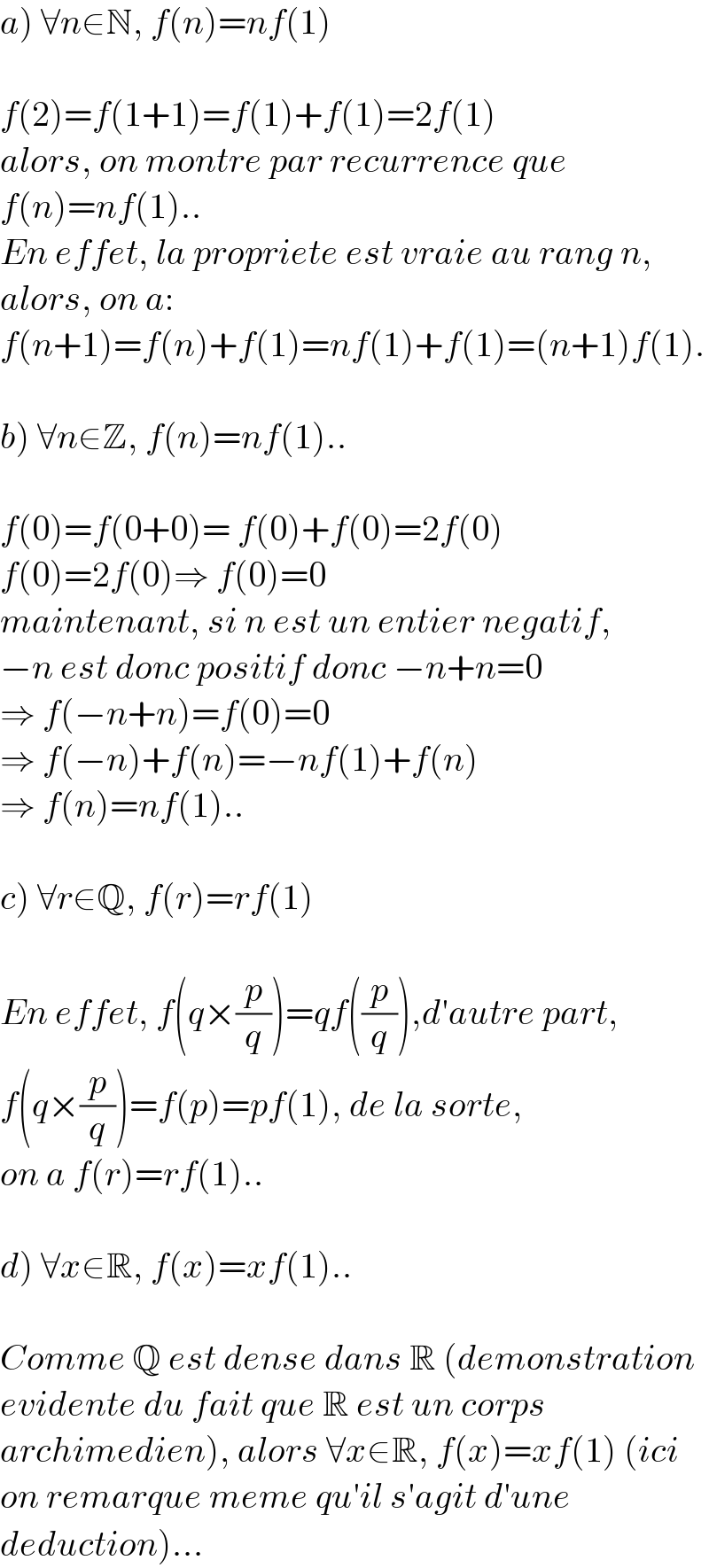
$$\left.{a}\right)\:\forall{n}\in\mathbb{N},\:{f}\left({n}\right)={nf}\left(\mathrm{1}\right) \\ $$$$ \\ $$$${f}\left(\mathrm{2}\right)={f}\left(\mathrm{1}+\mathrm{1}\right)={f}\left(\mathrm{1}\right)+{f}\left(\mathrm{1}\right)=\mathrm{2}{f}\left(\mathrm{1}\right) \\ $$$${alors},\:{on}\:{montre}\:{par}\:{recurrence}\:{que} \\ $$$${f}\left({n}\right)={nf}\left(\mathrm{1}\right).. \\ $$$${En}\:{effet},\:{la}\:{propriete}\:{est}\:{vraie}\:{au}\:{rang}\:{n}, \\ $$$${alors},\:{on}\:{a}:\: \\ $$$${f}\left({n}+\mathrm{1}\right)={f}\left({n}\right)+{f}\left(\mathrm{1}\right)={nf}\left(\mathrm{1}\right)+{f}\left(\mathrm{1}\right)=\left({n}+\mathrm{1}\right){f}\left(\mathrm{1}\right). \\ $$$$ \\ $$$$\left.{b}\right)\:\forall{n}\in\mathbb{Z},\:{f}\left({n}\right)={nf}\left(\mathrm{1}\right).. \\ $$$$ \\ $$$${f}\left(\mathrm{0}\right)={f}\left(\mathrm{0}+\mathrm{0}\right)=\:{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{0}\right)=\mathrm{2}{f}\left(\mathrm{0}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{2}{f}\left(\mathrm{0}\right)\Rightarrow\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${maintenant},\:{si}\:{n}\:{est}\:{un}\:{entier}\:{negatif}, \\ $$$$−{n}\:{est}\:{donc}\:{positif}\:{donc}\:−{n}+{n}=\mathrm{0} \\ $$$$\Rightarrow\:{f}\left(−{n}+{n}\right)={f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{f}\left(−{n}\right)+{f}\left({n}\right)=−{nf}\left(\mathrm{1}\right)+{f}\left({n}\right) \\ $$$$\Rightarrow\:{f}\left({n}\right)={nf}\left(\mathrm{1}\right).. \\ $$$$ \\ $$$$\left.{c}\right)\:\forall{r}\in\mathbb{Q},\:{f}\left({r}\right)={rf}\left(\mathrm{1}\right) \\ $$$$ \\ $$$${En}\:{effet},\:{f}\left({q}×\frac{{p}}{{q}}\right)={qf}\left(\frac{{p}}{{q}}\right),{d}'{autre}\:{part}, \\ $$$${f}\left({q}×\frac{{p}}{{q}}\right)={f}\left({p}\right)={pf}\left(\mathrm{1}\right),\:{de}\:{la}\:{sorte}, \\ $$$${on}\:{a}\:{f}\left({r}\right)={rf}\left(\mathrm{1}\right).. \\ $$$$ \\ $$$$\left.{d}\right)\:\forall{x}\in\mathbb{R},\:{f}\left({x}\right)={xf}\left(\mathrm{1}\right).. \\ $$$$ \\ $$$${Comme}\:\mathbb{Q}\:{est}\:{dense}\:{dans}\:\mathbb{R}\:\left({demonstration}\right. \\ $$$${evidente}\:{du}\:{fait}\:{que}\:\mathbb{R}\:{est}\:{un}\:{corps} \\ $$$$\left.{archimedien}\right),\:{alors}\:\forall{x}\in\mathbb{R},\:{f}\left({x}\right)={xf}\left(\mathrm{1}\right)\:\left({ici}\right. \\ $$$${on}\:{remarque}\:{meme}\:{qu}'{il}\:{s}'{agit}\:{d}'{une}\: \\ $$$$\left.{deduction}\right)... \\ $$
