Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 155479 by mathdanisur last updated on 01/Oct/21

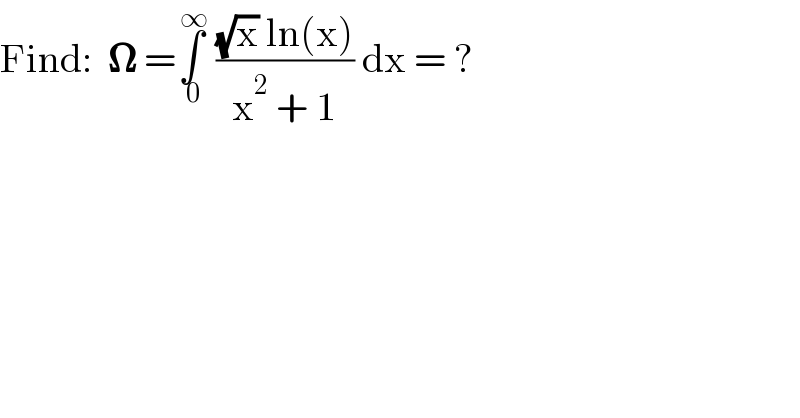
Find: 𝛀 =∫_( 0) ^( ∞) (((√x) ln(x))/(x^2 + 1)) dx = ?

$$\mathrm{Find}:\:\:\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\sqrt{\mathrm{x}}\:\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:\mathrm{dx}\:=\:? \\ $$

Commented by mathdanisur last updated on 01/Oct/21

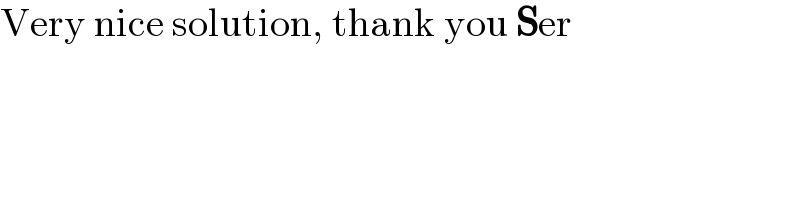
Very nice solution, thank you Ser

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{solution},\:\mathrm{thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$

Commented by aliyn last updated on 01/Oct/21

𝛀 = ∫_0 ^( ∞) (((√( x)) ln(x))/(x^2 +1)) dx Solution: 𝛀 = Re ( ∫_0 ^( ∞) (((√( x)) ln(x))/(x^2 +1)) dx ) x^2 +1 = 0 β‡’ x = Β± i Res(f,βˆ’i) = lim_(xβ†’βˆ’i) (x+i) Γ— (((√x) ln(x))/((xβˆ’i)(x+i))) = (((√(βˆ’i)) ln(βˆ’i))/(βˆ’2i)) Since: (√(βˆ’i)) = (βˆ’i)^(1/2) = (e^(βˆ’i(𝛑/2)) )^(1/2) = e^(βˆ’i(𝛑/4)) = cos((𝛑/4)) βˆ’ i sin((𝛑/4)) = (1/( (√2))) βˆ’ i (1/( (√2))) ln(βˆ’i) = ln ( e^(βˆ’i(𝛑/2)) ) = βˆ’ i (𝛑/2) ∴ (√(βˆ’i)) ln(βˆ’i) = βˆ’ i (𝛑/(2 (√( 2)))) βˆ’ (𝛑/(2 (√( 2)))) ∴ 𝛀 = Re ( 2𝛑i Γ—Res( f,βˆ’i) )= ((βˆ’((2𝛑^2 )/(2(√( 2)))) βˆ’ i ((2𝛑^2 )/(2 (√2))))/(βˆ’ 2 i)) = (𝛑^2 /( 2 (√( 2)))) ∴ ∴ 𝛀 = (𝛑^2 /(2 (√( 2)))) ⟨ M . T ⟩

$$\boldsymbol{\Omega}\:=\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\sqrt{\:\boldsymbol{{x}}}\:\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}\:\boldsymbol{{dx}} \\ $$$$ \\ $$$$\boldsymbol{{Solution}}: \\ $$$$ \\ $$$$\boldsymbol{\Omega}\:=\:\boldsymbol{{Re}}\:\left(\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\sqrt{\:\boldsymbol{{x}}}\:\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}\:\boldsymbol{{dx}}\:\right) \\ $$$$ \\ $$$$\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{0}\:\Rightarrow\:\boldsymbol{{x}}\:=\:\pm\:\boldsymbol{{i}}\: \\ $$$$ \\ $$$$\boldsymbol{{Res}}\left(\boldsymbol{{f}},βˆ’\boldsymbol{{i}}\right)\:=\:\boldsymbol{{lim}}_{\boldsymbol{{x}}\rightarrowβˆ’\boldsymbol{{i}}} \:\left(\boldsymbol{{x}}+\boldsymbol{{i}}\right)\:Γ—\:\frac{\sqrt{\boldsymbol{{x}}}\:\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)}{\left(\boldsymbol{{x}}βˆ’\boldsymbol{{i}}\right)\left(\boldsymbol{{x}}+\boldsymbol{{i}}\right)}\:=\:\frac{\sqrt{βˆ’\boldsymbol{{i}}}\:\boldsymbol{{ln}}\left(βˆ’\boldsymbol{{i}}\right)}{βˆ’\mathrm{2}\boldsymbol{{i}}} \\ $$$$ \\ $$$$\boldsymbol{{Since}}:\:\sqrt{βˆ’\boldsymbol{{i}}}\:=\:\left(βˆ’\boldsymbol{{i}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\left(\boldsymbol{{e}}^{βˆ’\boldsymbol{{i}}\frac{\boldsymbol{\pi}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\:\boldsymbol{{e}}^{βˆ’\boldsymbol{{i}}\frac{\boldsymbol{\pi}}{\mathrm{4}}} \:=\:\boldsymbol{{cos}}\left(\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)\:βˆ’\:\boldsymbol{{i}}\:\boldsymbol{{sin}}\left(\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:βˆ’\:\boldsymbol{{i}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\: \\ $$$$ \\ $$$$\boldsymbol{{ln}}\left(βˆ’\boldsymbol{{i}}\right)\:=\:\boldsymbol{{ln}}\:\left(\:\boldsymbol{{e}}^{βˆ’\boldsymbol{{i}}\frac{\boldsymbol{\pi}}{\mathrm{2}}} \right)\:=\:βˆ’\:\boldsymbol{{i}}\:\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$ \\ $$$$\therefore\:\sqrt{βˆ’\boldsymbol{{i}}}\:\boldsymbol{{ln}}\left(βˆ’\boldsymbol{{i}}\right)\:=\:βˆ’\:\boldsymbol{{i}}\:\frac{\boldsymbol{\pi}}{\mathrm{2}\:\sqrt{\:\mathrm{2}}}\:βˆ’\:\frac{\boldsymbol{\pi}}{\mathrm{2}\:\sqrt{\:\mathrm{2}}}\: \\ $$$$ \\ $$$$\therefore\:\boldsymbol{\Omega}\:=\:\boldsymbol{{Re}}\:\left(\:\mathrm{2}\boldsymbol{\pi{i}}\:Γ—\boldsymbol{{Res}}\left(\:\boldsymbol{{f}},βˆ’\boldsymbol{{i}}\right)\:\right)=\:\frac{βˆ’\frac{\mathrm{2}\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{2}\sqrt{\:\mathrm{2}}}\:βˆ’\:\boldsymbol{{i}}\:\frac{\mathrm{2}\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{2}\:\sqrt{\mathrm{2}}}}{βˆ’\:\mathrm{2}\:\boldsymbol{{i}}}\:=\:\:\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\:\mathrm{2}\:\sqrt{\:\mathrm{2}}}\:\: \\ $$$$ \\ $$$$\therefore\:\therefore\:\boldsymbol{\Omega}\:=\:\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{2}\:\sqrt{\:\mathrm{2}}}\: \\ $$$$ \\ $$$$\:\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$

Commented by mindispower last updated on 01/Oct/21

Hello sir i hop all going well Nice solution By using Residu Theorem have a nice day

$${Hello}\:{sir}\:{i}\:{hop}\:{all}\:{going}\:{well} \\ $$$${Nice}\:{solution}\:{By}\:{using}\:{Residu}\:{Theorem} \\ $$$${have}\:{a}\:{nice}\:{day} \\ $$

Commented by aliyn last updated on 01/Oct/21

thank you sir !

$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}}\:! \\ $$

Commented by tabata last updated on 01/Oct/21

thank you sir

$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$

Answered by mindispower last updated on 01/Oct/21

Ξ©=(βˆ‚/βˆ‚a)∫_0 ^∞ (x^a /(1+x^2 ))dx∣_(a=(1/2)) ∫_0 ^∞ (x^a /(1+x^2 ))dx=∫_0 ^∞ (u^(a/2) /(1+u)).(du/(2(√u))) =(1/2)∫_0 ^∞ (u^(((a+1)/2)βˆ’1) /(1+u))du=f(a) recallΞ²(x,y)=∫_0 ^∞ (t^(xβˆ’1) /((1+t)^(x+y) ))dx f(a)=((Ξ²(((a+1)/2),((1βˆ’a)/2)))/2)=(1/2).(Ξ²(((1+a)/2),1βˆ’((1+a)/2)) =(1/2).(Ο€/(sin(((1+a)/2)Ο€)))=(Ο€/(2cos(((Ο€a)/2)))) Ξ©=(Ο€^2 /4).((sin(((Ο€a)/2)))/(cos^2 (((Ο€a)/2))))∣a=(1/2) =(Ο€^2 /4).(√2)=(Ο€^2 /(2(√2)))

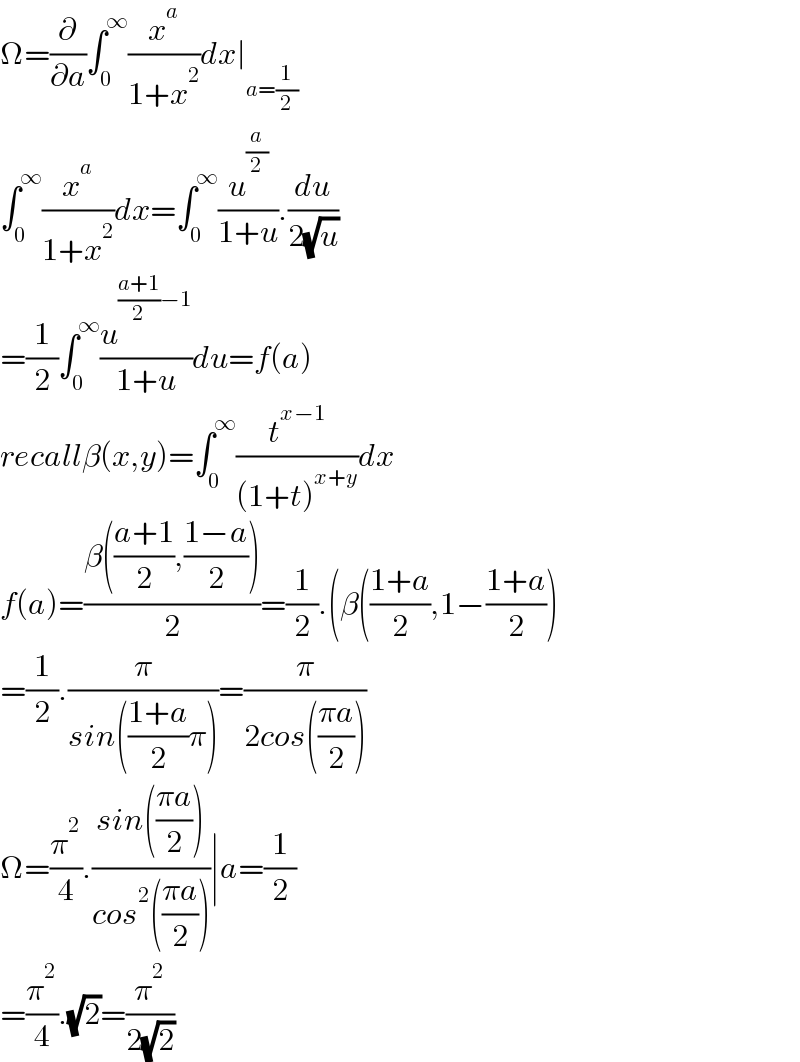
$$\Omega=\frac{\partial}{\partial{a}}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\mid_{{a}=\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{{a}}{\mathrm{2}}} }{\mathrm{1}+{u}}.\frac{{du}}{\mathrm{2}\sqrt{{u}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}βˆ’\mathrm{1}} }{\mathrm{1}+{u}}{du}={f}\left({a}\right) \\ $$$${recall}\beta\left({x},{y}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}βˆ’\mathrm{1}} }{\left(\mathrm{1}+{t}\right)^{{x}+{y}} }{dx} \\ $$$${f}\left({a}\right)=\frac{\beta\left(\frac{{a}+\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}βˆ’{a}}{\mathrm{2}}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}.\left(\beta\left(\frac{\mathrm{1}+{a}}{\mathrm{2}},\mathrm{1}βˆ’\frac{\mathrm{1}+{a}}{\mathrm{2}}\right)\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{{sin}\left(\frac{\mathrm{1}+{a}}{\mathrm{2}}\pi\right)}=\frac{\pi}{\mathrm{2}{cos}\left(\frac{\pi{a}}{\mathrm{2}}\right)} \\ $$$$\Omega=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}.\frac{{sin}\left(\frac{\pi{a}}{\mathrm{2}}\right)}{{cos}^{\mathrm{2}} \left(\frac{\pi{a}}{\mathrm{2}}\right)}\mid{a}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}.\sqrt{\mathrm{2}}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$

Commented by mathdanisur last updated on 01/Oct/21

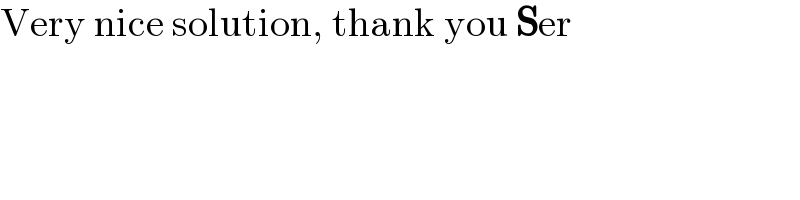
Very nice solution, thank you Ser

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{solution},\:\mathrm{thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$

Commented by mindispower last updated on 04/Oct/21

thanks Sir Withe plesur

$${thanks}\:{Sir}\:{Withe}\:{plesur} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com