Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 156867 by cortano last updated on 16/Oct/21

Answered by qaz last updated on 16/Oct/21

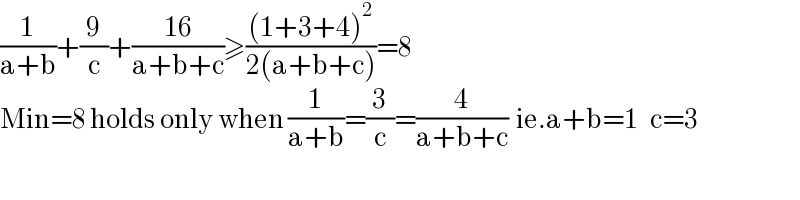
$$\frac{1}{\mathrm{a}+\mathrm{b}}+\frac{9}{\mathrm{c}}+\frac{16}{\mathrm{a}+\mathrm{b}+\mathrm{c}}⩾\frac{{(1+3+4)}^2}{2(\mathrm{a}+\mathrm{b}+\mathrm{c})}=8$$$$\mathrm{Min}=8\mathrm{holds}\mathrm{only}\mathrm{when}\frac{1}{\mathrm{a}+\mathrm{b}}=\frac{3}{\mathrm{c}}=\frac{4}{\mathrm{a}+\mathrm{b}+\mathrm{c}}\mathrm{ie}.\mathrm{a}+\mathrm{b}=1\mathrm{c}=3$$

Commented by cortano last updated on 16/Oct/21

$$Tittuslemma$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com