
Question Number 1573 by 123456 last updated on 20/Aug/15

$$\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}\:\underset{\mathrm{0}} {\overset{\epsilon} {\int}}\epsilon^{−{t}} {dt}=? \\ $$
Commented by 112358 last updated on 21/Aug/15
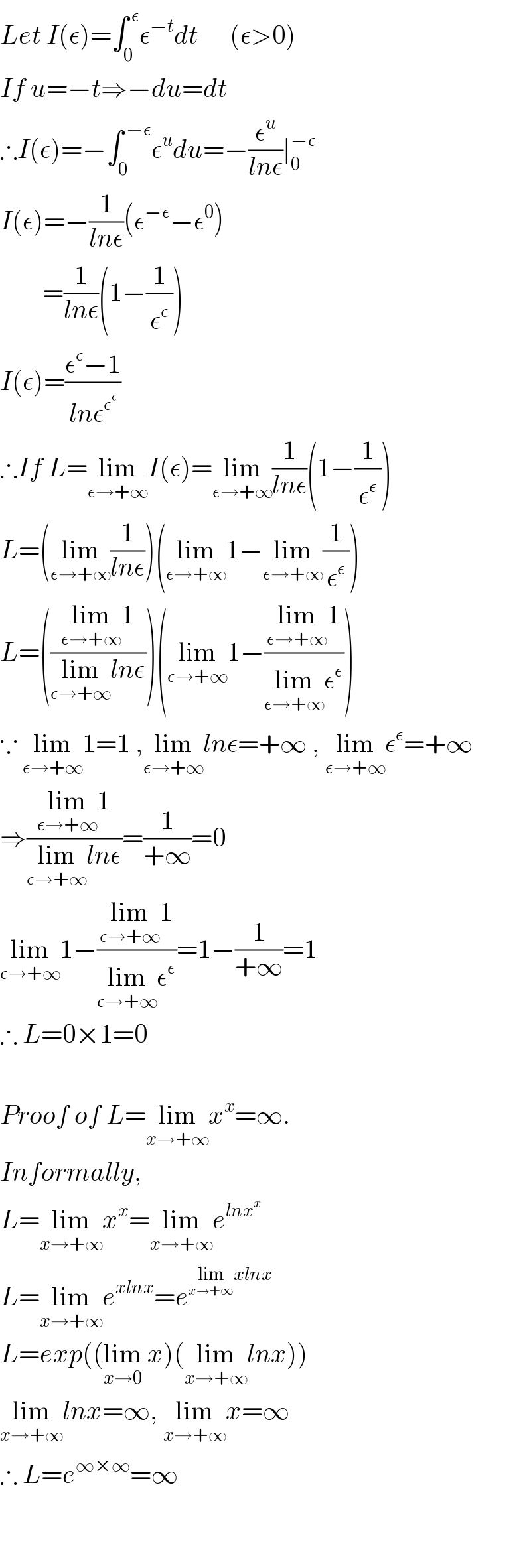
$${Let}\:{I}\left(\epsilon\right)=\int_{\mathrm{0}} ^{\:\epsilon} \epsilon^{−{t}} {dt}\:\:\:\:\:\:\left(\epsilon>\mathrm{0}\right) \\ $$$${If}\:{u}=−{t}\Rightarrow−{du}={dt} \\ $$$$\therefore{I}\left(\epsilon\right)=−\int_{\mathrm{0}} ^{\:−\epsilon} \epsilon^{{u}} {du}=−\frac{\epsilon^{{u}} }{{ln}\epsilon}\mid_{\mathrm{0}} ^{−\epsilon} \\ $$$${I}\left(\epsilon\right)=−\frac{\mathrm{1}}{{ln}\epsilon}\left(\epsilon^{−\epsilon} −\epsilon^{\mathrm{0}} \right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{ln}\epsilon}\left(\mathrm{1}−\frac{\mathrm{1}}{\epsilon^{\epsilon} }\right) \\ $$$${I}\left(\epsilon\right)=\frac{\epsilon^{\epsilon} −\mathrm{1}}{{ln}\epsilon^{\epsilon^{\epsilon} } } \\ $$$$\therefore{If}\:{L}=\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}{I}\left(\epsilon\right)=\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{ln}\epsilon}\left(\mathrm{1}−\frac{\mathrm{1}}{\epsilon^{\epsilon} }\right) \\ $$$${L}=\left(\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{ln}\epsilon}\right)\left(\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}1}−\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\epsilon^{\epsilon} }\right) \\ $$$${L}=\left(\frac{\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}1}}{\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}{ln}\epsilon}\right)\left(\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}1}−\frac{\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}1}}{\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}\epsilon^{\epsilon} }\right) \\ $$$$\because\:\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}1}=\mathrm{1}\:,\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}{ln}\epsilon=+\infty\:,\:\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}\epsilon^{\epsilon} =+\infty\:\: \\ $$$$\Rightarrow\frac{\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}1}}{\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}{ln}\epsilon}=\frac{\mathrm{1}}{+\infty}=\mathrm{0} \\ $$$$\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}1}−\frac{\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}1}}{\underset{\epsilon\rightarrow+\infty} {\mathrm{lim}}\epsilon^{\epsilon} }=\mathrm{1}−\frac{\mathrm{1}}{+\infty}=\mathrm{1} \\ $$$$\therefore\:{L}=\mathrm{0}×\mathrm{1}=\mathrm{0}\:\: \\ $$$$ \\ $$$${Proof}\:{of}\:{L}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{x}^{{x}} =\infty.\: \\ $$$${Informally}, \\ $$$${L}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{x}^{{x}} =\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{e}^{{lnx}^{{x}} } \\ $$$${L}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{e}^{{xlnx}} ={e}^{\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{xlnx}} \\ $$$${L}={exp}\left(\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}\right)\left(\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{lnx}\right)\right) \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{lnx}=\infty,\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{x}=\infty \\ $$$$\therefore\:{L}={e}^{\infty×\infty} =\infty \\ $$$$ \\ $$$$ \\ $$
