Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 157749 by naka3546 last updated on 27/Oct/21

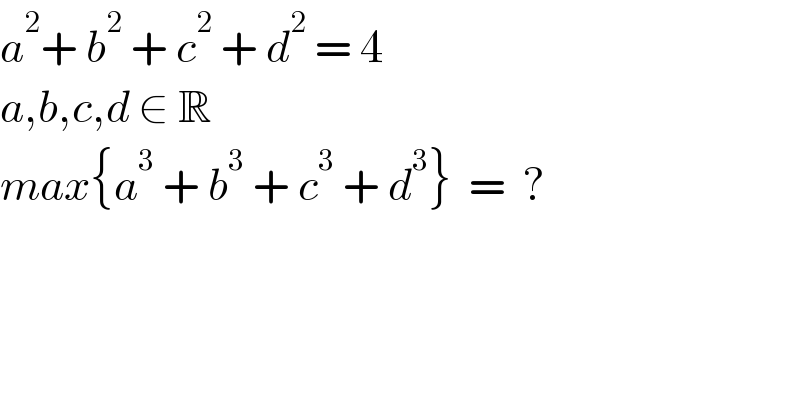
a^2 + b^2 + c^2 + d^2 = 4 a,b,c,d ∈ R max{a^3 + b^3 + c^3 + d^3 } = ?

$${a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} \:+\:{d}^{\mathrm{2}} \:=\:\mathrm{4} \\ $$$${a},{b},{c},{d}\:\in\:\mathbb{R} \\ $$$${max}\left\{{a}^{\mathrm{3}} \:+\:{b}^{\mathrm{3}} \:+\:{c}^{\mathrm{3}} \:+\:{d}^{\mathrm{3}} \right\}\:\:=\:\:? \\ $$

Commented by naka3546 last updated on 28/Oct/21

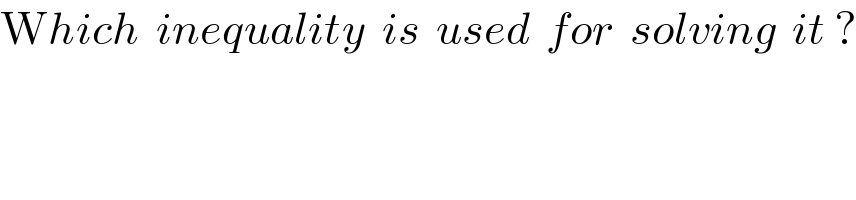
Which inequality is used for solving it ?

$$\mathrm{W}{hich}\:\:{inequality}\:\:{is}\:\:{used}\:\:{for}\:\:{solving}\:\:{it}\:? \\ $$

Commented by mr W last updated on 27/Oct/21

max=8

$${max}=\mathrm{8} \\ $$

Commented by naka3546 last updated on 27/Oct/21

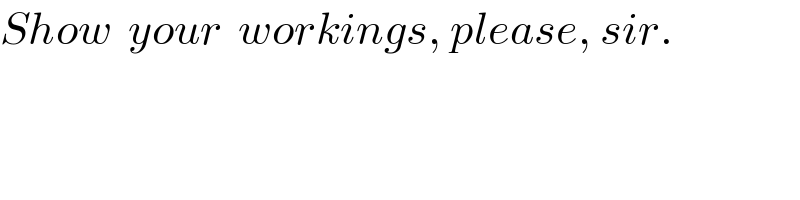
Show your workings, please, sir.

$${Show}\:\:{your}\:\:{workings},\:{please},\:{sir}. \\ $$

Commented by naka3546 last updated on 27/Oct/21

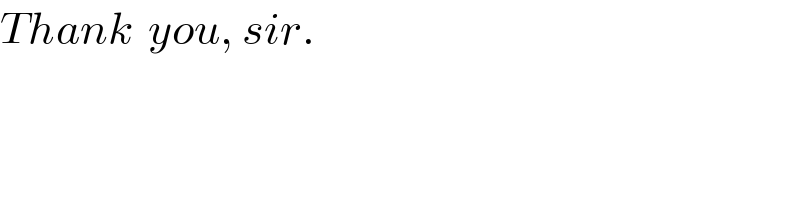
Thank you, sir.

$${Thank}\:\:{you},\:{sir}. \\ $$

Commented by mr W last updated on 27/Oct/21

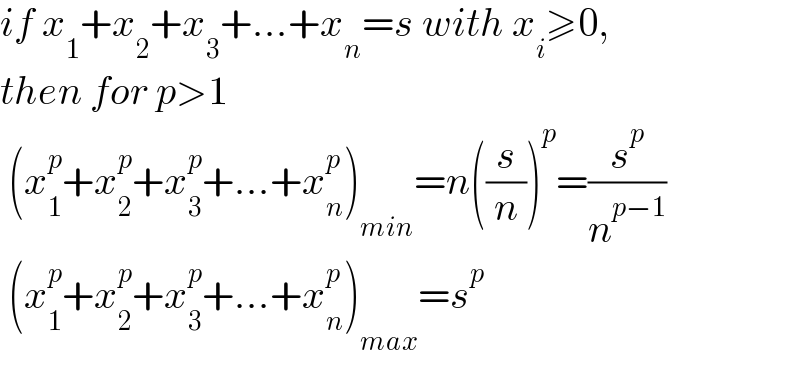
if x_1 +x_2 +x_3 +...+x_n =s with x_i ≥0, then for p>1 (x_1 ^p +x_2 ^p +x_3 ^p +...+x_n ^p )_(min) =n((s/n))^p =(s^p /n^(p−1) ) (x_1 ^p +x_2 ^p +x_3 ^p +...+x_n ^p )_(max) =s^p

$${if}\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +...+{x}_{{n}} ={s}\:{with}\:{x}_{{i}} \geqslant\mathrm{0}, \\ $$$${then}\:{for}\:{p}>\mathrm{1} \\ $$$$\:\left({x}_{\mathrm{1}} ^{{p}} +{x}_{\mathrm{2}} ^{{p}} +{x}_{\mathrm{3}} ^{{p}} +...+{x}_{{n}} ^{{p}} \right)_{{min}} ={n}\left(\frac{{s}}{{n}}\right)^{{p}} =\frac{{s}^{{p}} }{{n}^{{p}−\mathrm{1}} } \\ $$$$\:\left({x}_{\mathrm{1}} ^{{p}} +{x}_{\mathrm{2}} ^{{p}} +{x}_{\mathrm{3}} ^{{p}} +...+{x}_{{n}} ^{{p}} \right)_{{max}} ={s}^{{p}} \\ $$

Commented by mr W last updated on 03/Aug/23

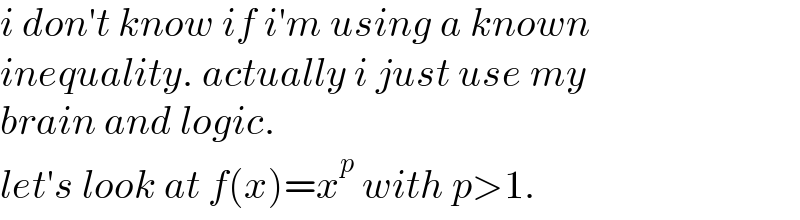
i don′t know if i′m using a known inequality. actually i just use my brain and logic. let′s look at f(x)=x^p with p>1.

$${i}\:{don}'{t}\:{know}\:{if}\:{i}'{m}\:{using}\:{a}\:{known} \\ $$$${inequality}.\:{actually}\:{i}\:{just}\:{use}\:{my} \\ $$$${brain}\:{and}\:{logic}. \\ $$$${let}'{s}\:{look}\:{at}\:{f}\left({x}\right)={x}^{{p}} \:{with}\:{p}>\mathrm{1}.\: \\ $$

Commented by mr W last updated on 28/Oct/21

Commented by mr W last updated on 03/Aug/23

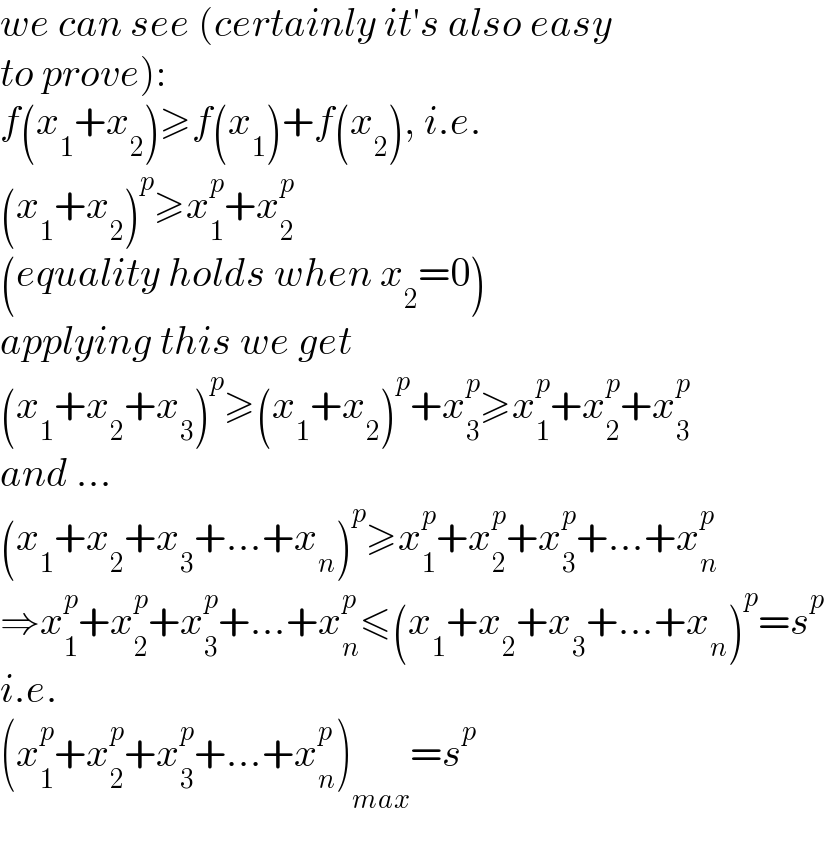
we can see (certainly it′s also easy to prove): f(x_1 +x_2 )≥f(x_1 )+f(x_2 ), i.e. (x_1 +x_2 )^p ≥x_1 ^p +x_2 ^p (equality holds when x_2 =0) applying this we get (x_1 +x_2 +x_3 )^p ≥(x_1 +x_2 )^p +x_3 ^p ≥x_1 ^p +x_2 ^p +x_3 ^p and ... (x_1 +x_2 +x_3 +...+x_n )^p ≥x_1 ^p +x_2 ^p +x_3 ^p +...+x_n ^p ⇒x_1 ^p +x_2 ^p +x_3 ^p +...+x_n ^p ≤(x_1 +x_2 +x_3 +...+x_n )^p =s^p i.e. (x_1 ^p +x_2 ^p +x_3 ^p +...+x_n ^p )_(max) =s^p

$${we}\:{can}\:{see}\:\left({certainly}\:{it}'{s}\:{also}\:{easy}\right. \\ $$$$\left.{to}\:{prove}\right): \\ $$$${f}\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)\geqslant{f}\left({x}_{\mathrm{1}} \right)+{f}\left({x}_{\mathrm{2}} \right),\:{i}.{e}. \\ $$$$\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{{p}} \geqslant{x}_{\mathrm{1}} ^{{p}} +{x}_{\mathrm{2}} ^{{p}} \\ $$$$\left({equality}\:{holds}\:{when}\:{x}_{\mathrm{2}} =\mathrm{0}\right) \\ $$$${applying}\:{this}\:{we}\:{get} \\ $$$$\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} \right)^{{p}} \geqslant\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{{p}} +{x}_{\mathrm{3}} ^{{p}} \geqslant{x}_{\mathrm{1}} ^{{p}} +{x}_{\mathrm{2}} ^{{p}} +{x}_{\mathrm{3}} ^{{p}} \\ $$$${and}\:... \\ $$$$\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +...+{x}_{{n}} \right)^{{p}} \geqslant{x}_{\mathrm{1}} ^{{p}} +{x}_{\mathrm{2}} ^{{p}} +{x}_{\mathrm{3}} ^{{p}} +...+{x}_{{n}} ^{{p}} \\ $$$$\Rightarrow{x}_{\mathrm{1}} ^{{p}} +{x}_{\mathrm{2}} ^{{p}} +{x}_{\mathrm{3}} ^{{p}} +...+{x}_{{n}} ^{{p}} \leqslant\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +...+{x}_{{n}} \right)^{{p}} ={s}^{{p}} \\ $$$${i}.{e}. \\ $$$$\left({x}_{\mathrm{1}} ^{{p}} +{x}_{\mathrm{2}} ^{{p}} +{x}_{\mathrm{3}} ^{{p}} +...+{x}_{{n}} ^{{p}} \right)_{{max}} ={s}^{{p}} \\ $$

Commented by mr W last updated on 28/Oct/21

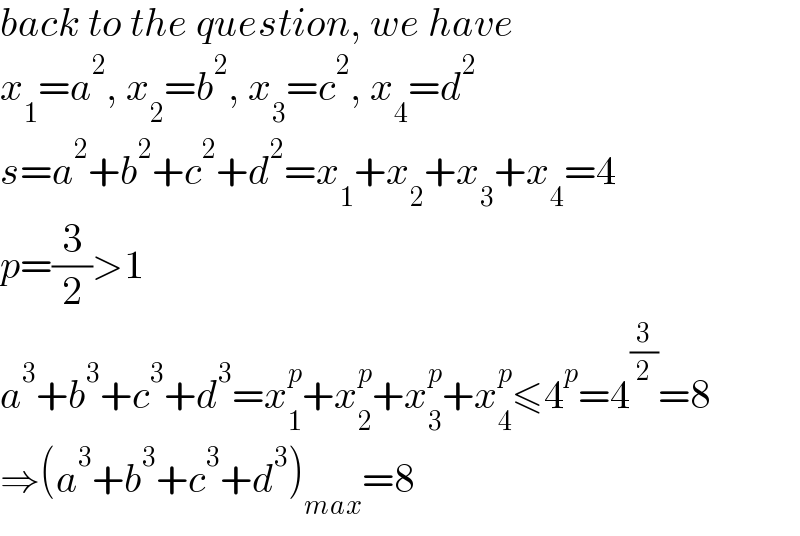
back to the question, we have x_1 =a^2 , x_2 =b^2 , x_3 =c^2 , x_4 =d^2 s=a^2 +b^2 +c^2 +d^2 =x_1 +x_2 +x_3 +x_4 =4 p=(3/2)>1 a^3 +b^3 +c^3 +d^3 =x_1 ^p +x_2 ^p +x_3 ^p +x_4 ^p ≤4^p =4^(3/2) =8 ⇒(a^3 +b^3 +c^3 +d^3 )_(max) =8

$${back}\:{to}\:{the}\:{question},\:{we}\:{have} \\ $$$${x}_{\mathrm{1}} ={a}^{\mathrm{2}} ,\:{x}_{\mathrm{2}} ={b}^{\mathrm{2}} ,\:{x}_{\mathrm{3}} ={c}^{\mathrm{2}} ,\:{x}_{\mathrm{4}} ={d}^{\mathrm{2}} \\ $$$${s}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} ={x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} =\mathrm{4} \\ $$$${p}=\frac{\mathrm{3}}{\mathrm{2}}>\mathrm{1} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +{d}^{\mathrm{3}} ={x}_{\mathrm{1}} ^{{p}} +{x}_{\mathrm{2}} ^{{p}} +{x}_{\mathrm{3}} ^{{p}} +{x}_{\mathrm{4}} ^{{p}} \leqslant\mathrm{4}^{{p}} =\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{8} \\ $$$$\Rightarrow\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +{d}^{\mathrm{3}} \right)_{{max}} =\mathrm{8} \\ $$

Commented by naka3546 last updated on 29/Oct/21

Thank you so much , sir.

$${Thank}\:\:{you}\:\:{so}\:\:{much}\:,\:\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com