Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 159465 by mnjuly1970 last updated on 17/Nov/21

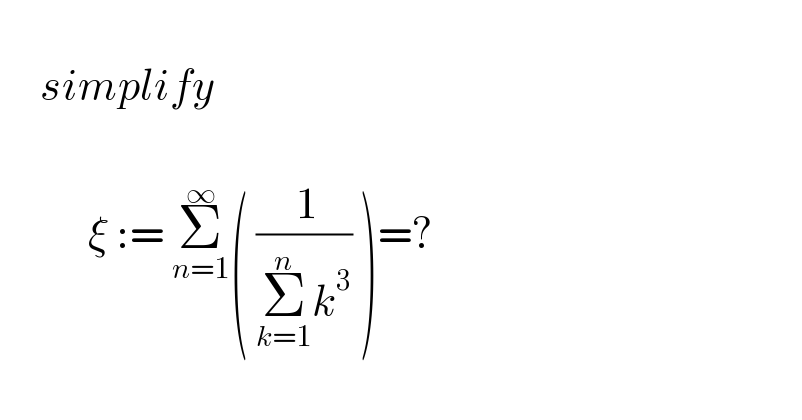
simplify ξ := Σ_(n=1) ^∞ ( (( 1)/(Σ_(k=1) ^n k^3 )) )=?

$$ \\ $$$$\:\:\:\:\:{simplify} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\xi\::=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\:\frac{\:\mathrm{1}}{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{3}} }\:\right)=? \\ $$$$ \\ $$

Answered by Ar Brandon last updated on 17/Nov/21

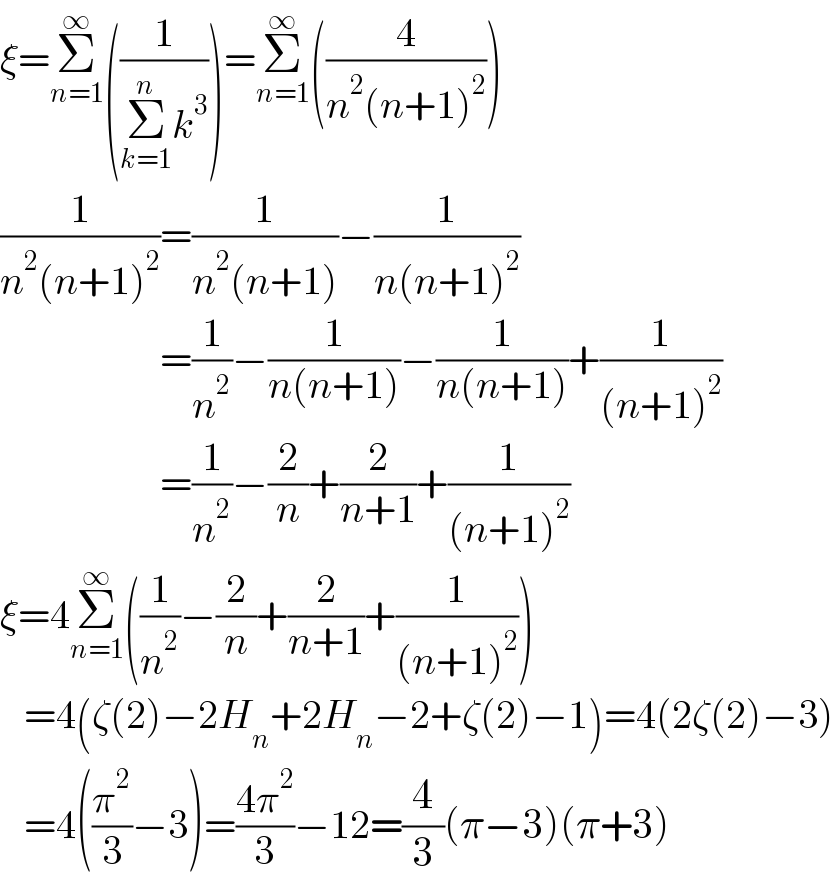
ξ=Σ_(n=1) ^∞ ((1/(Σ_(k=1) ^n k^3 )))=Σ_(n=1) ^∞ ((4/(n^2 (n+1)^2 ))) (1/(n^2 (n+1)^2 ))=(1/(n^2 (n+1)))−(1/(n(n+1)^2 )) =(1/n^2 )−(1/(n(n+1)))−(1/(n(n+1)))+(1/((n+1)^2 )) =(1/n^2 )−(2/n)+(2/(n+1))+(1/((n+1)^2 )) ξ=4Σ_(n=1) ^∞ ((1/n^2 )−(2/n)+(2/(n+1))+(1/((n+1)^2 ))) =4(ζ(2)−2H_n +2H_n −2+ζ(2)−1)=4(2ζ(2)−3) =4((π^2 /3)−3)=((4π^2 )/3)−12=(4/3)(π−3)(π+3)

$$\xi=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{3}} }\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{4}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{2}}{{n}}+\frac{\mathrm{2}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\xi=\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{2}}{{n}}+\frac{\mathrm{2}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\:\:\:=\mathrm{4}\left(\zeta\left(\mathrm{2}\right)−\mathrm{2}{H}_{{n}} +\mathrm{2}{H}_{{n}} −\mathrm{2}+\zeta\left(\mathrm{2}\right)−\mathrm{1}\right)=\mathrm{4}\left(\mathrm{2}\zeta\left(\mathrm{2}\right)−\mathrm{3}\right) \\ $$$$\:\:\:=\mathrm{4}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{3}\right)=\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{12}=\frac{\mathrm{4}}{\mathrm{3}}\left(\pi−\mathrm{3}\right)\left(\pi+\mathrm{3}\right) \\ $$

Commented by mnjuly1970 last updated on 17/Nov/21

thanks alot sir brandon.mercey

$$\:\:\:{thanks}\:{alot}\:{sir}\:{brandon}.{mercey} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com