Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 15969 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Jun/17

3 circles have the same center point. there is a equilateral triangle ,such that any vertex located on one circle as showen. 1)how can we draw such triangle? 2)find area of this triangle in terms of those 3 circle radiuses.

$$\mathrm{3}\:{circles}\:{have}\:{the}\:{same}\:{center}\:{point}. \\ $$$${there}\:{is}\:{a}\:{equilateral}\:{triangle}\:,{such}\:{that} \\ $$$${any}\:{vertex}\:{located}\:{on}\:{one}\:{circle}\:{as}\:{showen}. \\ $$$$\left.\mathrm{1}\right){how}\:{can}\:{we}\:{draw}\:{such}\:{triangle}? \\ $$$$\left.\mathrm{2}\right){find}\:{area}\:{of}\:{this}\:{triangle}\:{in}\:{terms}\:{of} \\ $$$${those}\:\mathrm{3}\:{circle}\:{radiuses}. \\ $$

Commented by mrW1 last updated on 18/Jun/17

you are right sir. that′s a typo.

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{sir}.\:\mathrm{that}'\mathrm{s}\:\mathrm{a}\:\mathrm{typo}. \\ $$

Commented by ajfour last updated on 18/Jun/17

sir in Q.15993 i had posted a solution to these 3circles question, does my answer compare with yours ?

$${sir}\:{in}\:{Q}.\mathrm{15993}\:{i}\:{had}\:{posted}\:{a}\: \\ $$$${solution}\:{to}\:{these}\:\mathrm{3}{circles}\:{question}, \\ $$$${does}\:{my}\:{answer}\:{compare}\:{with} \\ $$$${yours}\:? \\ $$$$ \\ $$

Commented by mrW1 last updated on 17/Jun/17

When we take a fixed point A on circle 1, and make it as a vertex from an equilateral triangle. The second vertex lies on circle 2. The track of the third vertex is then also a circle. Using this property we can draw an equilateral triangle on three circles. Fixed point on circle 1 is A. On circle 2 we select some points, at least 3: P_1 ,P_2 ,P_3 . We construct 3 equilateral triangles with AP_1 ,AP_2 ,AP_3 . The third point of the equilateral triangles are Q_1 ,Q_2 ,Q_(3.) These points should be on the same direction. Through Q_1 ,Q_2 ,Q_3 a new circle can be constructed. This circle intersects with the circle 3 at point C (as well as C′). Point C (C′) is the vertex on circle 3. With point A on circle 1 and C on circle 3 we can easily find the vertex B (as well as B′) on circle 2. If the fourth circle doesn′t intersect with circle 3 it means there is no solution. If it tangents the circle 3 there is only one equilateral triangle, other− wise there are two.

$$\mathrm{When}\:\mathrm{we}\:\mathrm{take}\:\mathrm{a}\:\mathrm{fixed}\:\mathrm{point}\:\mathrm{A}\:\mathrm{on}\:\mathrm{circle}\:\mathrm{1}, \\ $$$$\mathrm{and}\:\mathrm{make}\:\mathrm{it}\:\mathrm{as}\:\mathrm{a}\:\mathrm{vertex}\:\mathrm{from}\:\mathrm{an} \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}.\:\mathrm{The}\:\mathrm{second} \\ $$$$\mathrm{vertex}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{circle}\:\mathrm{2}.\:\mathrm{The}\:\mathrm{track}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{third}\:\mathrm{vertex}\:\mathrm{is}\:\mathrm{then}\:\mathrm{also}\:\mathrm{a}\:\mathrm{circle}.\: \\ $$$$ \\ $$$$\mathrm{Using}\:\mathrm{this}\:\mathrm{property}\:\mathrm{we}\:\mathrm{can}\:\mathrm{draw}\:\mathrm{an} \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{on}\:\mathrm{three}\:\mathrm{circles}. \\ $$$$ \\ $$$$\mathrm{Fixed}\:\mathrm{point}\:\mathrm{on}\:\mathrm{circle}\:\mathrm{1}\:\mathrm{is}\:\mathrm{A}. \\ $$$$\mathrm{On}\:\mathrm{circle}\:\mathrm{2}\:\mathrm{we}\:\mathrm{select}\:\mathrm{some}\:\mathrm{points},\:\mathrm{at} \\ $$$$\mathrm{least}\:\mathrm{3}:\:\mathrm{P}_{\mathrm{1}} ,\mathrm{P}_{\mathrm{2}} ,\mathrm{P}_{\mathrm{3}} . \\ $$$$\mathrm{We}\:\mathrm{construct}\:\mathrm{3}\:\mathrm{equilateral}\:\mathrm{triangles} \\ $$$$\mathrm{with}\:\mathrm{AP}_{\mathrm{1}} ,\mathrm{AP}_{\mathrm{2}} ,\mathrm{AP}_{\mathrm{3}} .\:\mathrm{The}\:\mathrm{third}\:\mathrm{point} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{equilateral}\:\mathrm{triangles}\:\mathrm{are}\:\mathrm{Q}_{\mathrm{1}} ,\mathrm{Q}_{\mathrm{2}} ,\mathrm{Q}_{\mathrm{3}.} \\ $$$$\mathrm{These}\:\mathrm{points}\:\mathrm{should}\:\mathrm{be}\:\mathrm{on}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{direction}. \\ $$$$ \\ $$$$\mathrm{Through}\:\mathrm{Q}_{\mathrm{1}} ,\mathrm{Q}_{\mathrm{2}} ,\mathrm{Q}_{\mathrm{3}} \:\mathrm{a}\:\mathrm{new}\:\mathrm{circle}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{constructed}.\:\mathrm{This}\:\mathrm{circle}\:\mathrm{intersects} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{3}\:\mathrm{at}\:\mathrm{point}\:\mathrm{C}\:\left(\mathrm{as}\:\mathrm{well}\right. \\ $$$$\left.\mathrm{as}\:\mathrm{C}'\right).\:\mathrm{Point}\:\mathrm{C}\:\left(\mathrm{C}'\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{vertex}\:\mathrm{on} \\ $$$$\mathrm{circle}\:\mathrm{3}. \\ $$$$\mathrm{With}\:\mathrm{point}\:\mathrm{A}\:\mathrm{on}\:\mathrm{circle}\:\mathrm{1}\:\mathrm{and}\:\mathrm{C}\:\mathrm{on} \\ $$$$\mathrm{circle}\:\mathrm{3}\:\mathrm{we}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{find}\:\mathrm{the}\:\mathrm{vertex} \\ $$$$\mathrm{B}\:\left(\mathrm{as}\:\mathrm{well}\:\mathrm{as}\:\mathrm{B}'\right)\:\mathrm{on}\:\mathrm{circle}\:\mathrm{2}. \\ $$$$ \\ $$$$\mathrm{If}\:\mathrm{the}\:\mathrm{fourth}\:\mathrm{circle}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{intersect} \\ $$$$\mathrm{with}\:\mathrm{circle}\:\mathrm{3}\:\mathrm{it}\:\mathrm{means}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no} \\ $$$$\mathrm{solution}.\:\mathrm{If}\:\mathrm{it}\:\mathrm{tangents}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{3}\:\mathrm{there} \\ $$$$\mathrm{is}\:\mathrm{only}\:\mathrm{one}\:\mathrm{equilateral}\:\mathrm{triangle},\:\mathrm{other}− \\ $$$$\mathrm{wise}\:\mathrm{there}\:\mathrm{are}\:\mathrm{two}. \\ $$

Commented by mrW1 last updated on 17/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 17/Jun/17

thank you very much my master. it is perfect answer. is there any solution by using complex numbers?what do you think?

$${thank}\:{you}\:{very}\:{much}\:{my}\:{master}. \\ $$$${it}\:{is}\:{perfect}\:{answer}. \\ $$$${is}\:{there}\:{any}\:{solution}\:{by}\:{using}\:{complex} \\ $$$${numbers}?{what}\:{do}\:{you}\:{think}? \\ $$

Commented by RasheedSoomro last updated on 17/Jun/17

Great knowledge!

$$\mathrm{Great}\:\mathrm{knowledge}! \\ $$

Commented by mrW1 last updated on 19/Jun/17

I got the formula to calculate the side length of the equilateral triangle analytically. Radius of circle 1 = a >0 Radius of circle 2 = b Radius of circle 3 = c let β=(b/a), γ=(c/a) The condition that such triangle(s) exists is a≤c≤a+b. The length of sides of the triangle is d=(a/2)(√(λ^2 +((√δ)±(√3))^2 )) with λ=(γ+β)(γ−β) δ=(γ+β+1)(1+β−γ)(γ−β+1)(γ+β−1) The area of the equilateral triangle is A=((√3)/4)d^2 =(((√3)a^2 )/(16))[λ^2 +((√δ)±(√3))^2 ]

$$\mathrm{I}\:\mathrm{got}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{side} \\ $$$$\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equilateral}\:\mathrm{triangle} \\ $$$$\mathrm{analytically}. \\ $$$$ \\ $$$$\mathrm{Radius}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{1}\:=\:\mathrm{a}\:>\mathrm{0} \\ $$$$\mathrm{Radius}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{2}\:=\:\mathrm{b} \\ $$$$\mathrm{Radius}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{3}\:=\:\mathrm{c} \\ $$$$\mathrm{let}\:\beta=\frac{\mathrm{b}}{\mathrm{a}},\:\gamma=\frac{\mathrm{c}}{\mathrm{a}} \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{condition}\:\mathrm{that}\:\mathrm{such}\:\mathrm{triangle}\left(\mathrm{s}\right) \\ $$$$\mathrm{exists}\:\mathrm{is}\:\mathrm{a}\leqslant\mathrm{c}\leqslant\mathrm{a}+\mathrm{b}. \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{length}\:\mathrm{of}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{is} \\ $$$$\mathrm{d}=\frac{\mathrm{a}}{\mathrm{2}}\sqrt{\lambda^{\mathrm{2}} +\left(\sqrt{\delta}\pm\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{with} \\ $$$$\lambda=\left(\gamma+\beta\right)\left(\gamma−\beta\right) \\ $$$$\delta=\left(\gamma+\beta+\mathrm{1}\right)\left(\mathrm{1}+\beta−\gamma\right)\left(\gamma−\beta+\mathrm{1}\right)\left(\gamma+\beta−\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{is} \\ $$$$\mathrm{A}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{d}^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}\mathrm{a}^{\mathrm{2}} }{\mathrm{16}}\left[\lambda^{\mathrm{2}} +\left(\sqrt{\delta}\pm\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \right] \\ $$

Commented by mrW1 last updated on 18/Jun/17

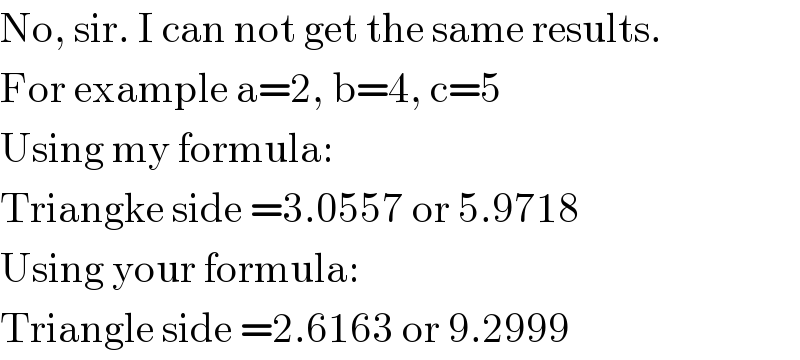
No, sir. I can not get the same results. For example a=2, b=4, c=5 Using my formula: Triangke side =3.0557 or 5.9718 Using your formula: Triangle side =2.6163 or 9.2999

$$\mathrm{No},\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{can}\:\mathrm{not}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{results}. \\ $$$$\mathrm{For}\:\mathrm{example}\:\mathrm{a}=\mathrm{2},\:\mathrm{b}=\mathrm{4},\:\mathrm{c}=\mathrm{5} \\ $$$$\mathrm{Using}\:\mathrm{my}\:\mathrm{formula}: \\ $$$$\mathrm{Triangke}\:\mathrm{side}\:=\mathrm{3}.\mathrm{0557}\:\mathrm{or}\:\mathrm{5}.\mathrm{9718} \\ $$$$\mathrm{Using}\:\mathrm{your}\:\mathrm{formula}: \\ $$$$\mathrm{Triangle}\:\mathrm{side}\:=\mathrm{2}.\mathrm{6163}\:\mathrm{or}\:\mathrm{9}.\mathrm{2999} \\ $$

Commented by ajfour last updated on 18/Jun/17

okay sir, i will check my solution and answer,thanks for an example to compare.

$${okay}\:{sir},\:{i}\:{will}\:{check}\:{my}\:{solution} \\ $$$${and}\:{answer},{thanks}\:{for}\:{an} \\ $$$${example}\:{to}\:{compare}. \\ $$

Commented by ajfour last updated on 19/Jun/17

amended my result sir, d^2 =(1/2)(a^2 +b^2 +c^2 ) ±((√3)/2)(√(2(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^4 +b^4 +c^4 ))) with a=b=c it gives correct answer, even for a=2, b=4, c=5 the answer matches with yours, but our expressions for side length dont convert (not by me). however in both these cases your condition c≥a+b , dont hold true. kindly verify this, Sir.

$${amended}\:{my}\:{result}\:{sir}, \\ $$$${d}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\:\:\:\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)} \\ $$$${with}\:{a}={b}={c}\:{it}\:{gives}\:{correct} \\ $$$${answer},\:{even}\:{for}\:{a}=\mathrm{2},\:{b}=\mathrm{4},\:{c}=\mathrm{5} \\ $$$${the}\:{answer}\:{matches}\:{with}\:{yours}, \\ $$$${but}\:{our}\:{expressions}\:{for}\:{side} \\ $$$${length}\:{dont}\:{convert}\:\left({not}\:{by}\:{me}\right). \\ $$$${however}\:{in}\:{both}\:{these}\:{cases}\:{your} \\ $$$${condition}\:{c}\geqslant{a}+{b}\:,\:{dont}\:{hold}\:{true}. \\ $$$${kindly}\:{verify}\:{this},\:{Sir}. \\ $$$$ \\ $$

Commented by mrW1 last updated on 19/Jun/17

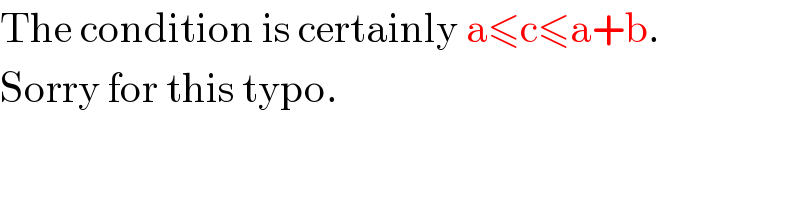
The condition is certainly a≤c≤a+b. Sorry for this typo.

$$\mathrm{The}\:\mathrm{condition}\:\mathrm{is}\:\mathrm{certainly}\:\mathrm{a}\leqslant\mathrm{c}\leqslant\mathrm{a}+\mathrm{b}. \\ $$$$\mathrm{Sorry}\:\mathrm{for}\:\mathrm{this}\:\mathrm{typo}. \\ $$

Commented by ajfour last updated on 19/Jun/17

what about checking my expression for side length of Δ,Sir ; for it qualifies well and is precise enough..kindly view my solution when i post it again, it might take two hours, i think .

$${what}\:{about}\:{checking}\:{my}\:{expression} \\ $$$${for}\:{side}\:{length}\:{of}\:\Delta,{Sir}\:;\:{for}\:{it} \\ $$$${qualifies}\:{well}\:{and}\:{is}\:{precise} \\ $$$${enough}..{kindly}\:{view}\:{my}\:{solution} \\ $$$${when}\:{i}\:{post}\:{it}\:{again},\:{it}\:{might}\:{take} \\ $$$${two}\:{hours},\:{i}\:{think}\:. \\ $$

Commented by mrW1 last updated on 19/Jun/17

sir, what is d in this expression? d^2 =(1/2)(a^2 +b^2 +c^2 ) ±((√3)/2)(√(2(a^2 +b^2 +c^2 )−(a^4 +b^4 +c^4 ))) with a=2,b=4,c=5 we have (√(2(a^2 +b^2 +c^2 )−(a^4 +b^4 +c^4 ))) =(√(2(2^2 +4^2 +5^2 )−(2^4 +4^4 +5^4 ))) =(√(−807)) this is not real. please check sir. for comparation please give me your expression for side length of the triangle which is d in my formula.

$$\mathrm{sir},\:\mathrm{what}\:\mathrm{is}\:\mathrm{d}\:\mathrm{in}\:\mathrm{this}\:\mathrm{expression}? \\ $$$${d}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\:\:\:\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)} \\ $$$$ \\ $$$$\mathrm{with}\:\mathrm{a}=\mathrm{2},\mathrm{b}=\mathrm{4},\mathrm{c}=\mathrm{5}\:\mathrm{we}\:\mathrm{have} \\ $$$$\:\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)} \\ $$$$\:=\sqrt{\mathrm{2}\left(\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} \right)−\left(\mathrm{2}^{\mathrm{4}} +\mathrm{4}^{\mathrm{4}} +\mathrm{5}^{\mathrm{4}} \right)} \\ $$$$=\sqrt{−\mathrm{807}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{real}. \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{sir}. \\ $$$$\mathrm{for}\:\mathrm{comparation}\:\mathrm{please}\:\mathrm{give}\:\mathrm{me} \\ $$$$\mathrm{your}\:\mathrm{expression}\:\mathrm{for}\:\mathrm{side}\:\mathrm{length}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{triangle}\:\mathrm{which}\:\mathrm{is}\:\mathrm{d}\:\mathrm{in}\:\mathrm{my}\:\mathrm{formula}. \\ $$

Commented by mrW1 last updated on 19/Jun/17

further simplification: λ=(γ+β)(γ−β) δ=(γ+β+1)(1+β−γ)(γ−β+1)(γ+β−1) δ=[(1+β)^2 −γ^2 ][γ^2 −(β−1)^2 ] =(β+1)^2 γ^2 −γ^4 −(β+1)^2 (β−1)^2 +(β−1)^2 γ^2 =[(β+1)^2 +(β−1)^2 ]γ^2 −γ^4 −(β+1)^2 (β−1)^2 =2(β^2 +1)γ^2 −γ^4 −β^4 +2β^2 −1 =2β^2 γ^2 +2γ^2 −γ^4 −β^4 +2β^2 −1 =2(β^2 γ^2 +β^2 +γ^2 )−(1+γ^4 +β^4 ) λ^2 =(γ^2 −β^2 )^2 =γ^4 +β^4 −2β^2 γ^2 λ^2 +((√δ)±(√3))^2 =λ^2 +δ+3±2(√(3δ)) =γ^4 +β^4 −2β^2 γ^2 +2β^2 γ^2 +2γ^2 −γ^4 −β^4 +2β^2 −1+3±2(√(3δ)) =2γ^2 +2β^2 +2±2(√(3δ)) =2(1+γ^2 +β^2 ±(√(3δ))) d=(a/(√2))(√(1+β^2 +γ^2 ±(√(3δ)))) d=(a/(√2))(√((1+β^2 +γ^2 )±(√3)×(√(2(β^2 +γ^2 +β^2 γ^2 )−(1+β^4 +γ^4 ))))) or d=(1/(√2))(√((a^2 +b^2 +c^2 )±(√(6(a^2 b^2 +b^2 c^2 +c^2 a^2 )−3(a^4 +b^4 +c^4 ))))) A=((√3)/4)d^2 =((√3)/8)[a^2 +b^2 +c^2 ±(√(6(a^2 b^2 +b^2 c^2 +c^2 a^2 )−3(a^4 +b^4 +c^4 )))]

$$\mathrm{further}\:\mathrm{simplification}: \\ $$$$\lambda=\left(\gamma+\beta\right)\left(\gamma−\beta\right) \\ $$$$\delta=\left(\gamma+\beta+\mathrm{1}\right)\left(\mathrm{1}+\beta−\gamma\right)\left(\gamma−\beta+\mathrm{1}\right)\left(\gamma+\beta−\mathrm{1}\right) \\ $$$$\delta=\left[\left(\mathrm{1}+\beta\right)^{\mathrm{2}} −\gamma^{\mathrm{2}} \right]\left[\gamma^{\mathrm{2}} −\left(\beta−\mathrm{1}\right)^{\mathrm{2}} \right] \\ $$$$=\left(\beta+\mathrm{1}\right)^{\mathrm{2}} \gamma^{\mathrm{2}} −\gamma^{\mathrm{4}} −\left(\beta+\mathrm{1}\right)^{\mathrm{2}} \left(\beta−\mathrm{1}\right)^{\mathrm{2}} +\left(\beta−\mathrm{1}\right)^{\mathrm{2}} \gamma^{\mathrm{2}} \\ $$$$=\left[\left(\beta+\mathrm{1}\right)^{\mathrm{2}} +\left(\beta−\mathrm{1}\right)^{\mathrm{2}} \right]\gamma^{\mathrm{2}} −\gamma^{\mathrm{4}} −\left(\beta+\mathrm{1}\right)^{\mathrm{2}} \left(\beta−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}\left(\beta^{\mathrm{2}} +\mathrm{1}\right)\gamma^{\mathrm{2}} −\gamma^{\mathrm{4}} −\beta^{\mathrm{4}} +\mathrm{2}\beta^{\mathrm{2}} −\mathrm{1} \\ $$$$=\mathrm{2}\beta^{\mathrm{2}} \gamma^{\mathrm{2}} +\mathrm{2}\gamma^{\mathrm{2}} −\gamma^{\mathrm{4}} −\beta^{\mathrm{4}} +\mathrm{2}\beta^{\mathrm{2}} −\mathrm{1} \\ $$$$=\mathrm{2}\left(\beta^{\mathrm{2}} \gamma^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)−\left(\mathrm{1}+\gamma^{\mathrm{4}} +\beta^{\mathrm{4}} \right) \\ $$$$ \\ $$$$\lambda^{\mathrm{2}} =\left(\gamma^{\mathrm{2}} −\beta^{\mathrm{2}} \right)^{\mathrm{2}} =\gamma^{\mathrm{4}} +\beta^{\mathrm{4}} −\mathrm{2}\beta^{\mathrm{2}} \gamma^{\mathrm{2}} \\ $$$$\lambda^{\mathrm{2}} +\left(\sqrt{\delta}\pm\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\lambda^{\mathrm{2}} +\delta+\mathrm{3}\pm\mathrm{2}\sqrt{\mathrm{3}\delta} \\ $$$$=\gamma^{\mathrm{4}} +\beta^{\mathrm{4}} −\mathrm{2}\beta^{\mathrm{2}} \gamma^{\mathrm{2}} +\mathrm{2}\beta^{\mathrm{2}} \gamma^{\mathrm{2}} +\mathrm{2}\gamma^{\mathrm{2}} −\gamma^{\mathrm{4}} −\beta^{\mathrm{4}} +\mathrm{2}\beta^{\mathrm{2}} −\mathrm{1}+\mathrm{3}\pm\mathrm{2}\sqrt{\mathrm{3}\delta} \\ $$$$=\mathrm{2}\gamma^{\mathrm{2}} +\mathrm{2}\beta^{\mathrm{2}} +\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{3}\delta} \\ $$$$=\mathrm{2}\left(\mathrm{1}+\gamma^{\mathrm{2}} +\beta^{\mathrm{2}} \pm\sqrt{\mathrm{3}\delta}\right) \\ $$$$ \\ $$$$\mathrm{d}=\frac{\mathrm{a}}{\sqrt{\mathrm{2}}}\sqrt{\mathrm{1}+\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \pm\sqrt{\mathrm{3}\delta}} \\ $$$$\mathrm{d}=\frac{\mathrm{a}}{\sqrt{\mathrm{2}}}\sqrt{\left(\mathrm{1}+\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)\pm\sqrt{\mathrm{3}}×\sqrt{\mathrm{2}\left(\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} +\beta^{\mathrm{2}} \gamma^{\mathrm{2}} \right)−\left(\mathrm{1}+\beta^{\mathrm{4}} +\gamma^{\mathrm{4}} \right)}} \\ $$$$\mathrm{or} \\ $$$$\mathrm{d}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\sqrt{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)\pm\sqrt{\mathrm{6}\left(\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} \right)−\mathrm{3}\left(\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \right)}} \\ $$$$\mathrm{A}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{d}^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}\left[\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \pm\sqrt{\mathrm{6}\left(\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} \right)−\mathrm{3}\left(\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} \right)}\right] \\ $$

Commented by mrW1 last updated on 19/Jun/17

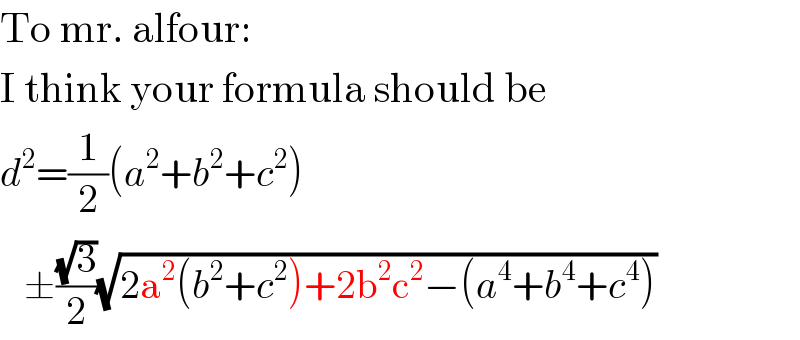
To mr. alfour: I think your formula should be d^2 =(1/2)(a^2 +b^2 +c^2 ) ±((√3)/2)(√(2a^2 (b^2 +c^2 )+2b^2 c^2 −(a^4 +b^4 +c^4 )))

$$\mathrm{To}\:\mathrm{mr}.\:\mathrm{alfour}: \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{your}\:\mathrm{formula}\:\mathrm{should}\:\mathrm{be} \\ $$$${d}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\:\:\:\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\sqrt{\mathrm{2a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)} \\ $$

Commented by ajfour last updated on 19/Jun/17

yes sir, it was this in my notebook but when i typed it to you i thought i remembered and typed wrong instead..Thank you sir. d is the same thing −side length.

$${yes}\:{sir},\:{it}\:{was}\:{this}\:{in}\:{my}\:{notebook} \\ $$$${but}\:{when}\:{i}\:{typed}\:{it}\:{to}\:{you}\:{i}\:{thought} \\ $$$${i}\:{remembered}\:{and}\:{typed}\:{wrong} \\ $$$${instead}..{Thank}\:{you}\:{sir}. \\ $$$$\:\:{d}\:{is}\:{the}\:{same}\:{thing}\:−{side}\:{length}. \\ $$

Commented by mrW1 last updated on 19/Jun/17

Then we have exactly the same result.

$$\mathrm{Then}\:\mathrm{we}\:\mathrm{have}\:\mathrm{exactly}\:\mathrm{the}\:\mathrm{same}\:\mathrm{result}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com