Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 160445 by HongKing last updated on 29/Nov/21

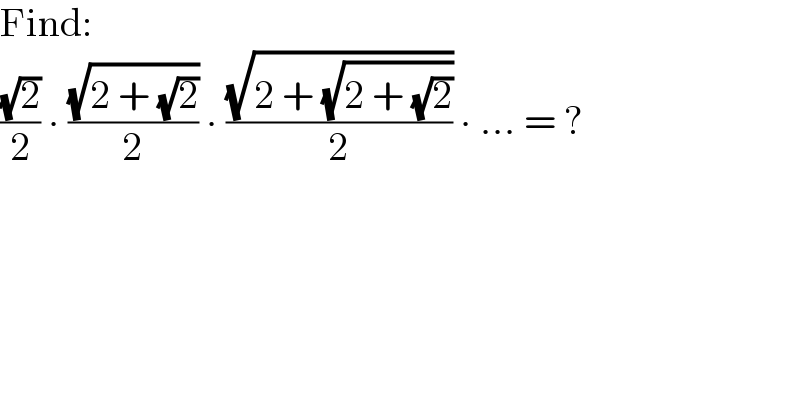
Find: ((√2)/2) ∙ ((√(2 + (√2)))/2) ∙ ((√(2 + (√(2 + (√2)))))/2) ∙ ... = ?

$$\mathrm{Find}: \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\centerdot\:\frac{\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}}}}{\mathrm{2}}\:\centerdot\:\frac{\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}\:+\:\sqrt{\mathrm{2}}}}}{\mathrm{2}}\:\centerdot\:...\:=\:? \\ $$

Commented by HongKing last updated on 29/Nov/21

Yes my dear Sir but how please

$$\mathrm{Yes}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{but}\:\mathrm{how}\:\mathrm{please} \\ $$

Commented by mr W last updated on 30/Nov/21

=(2/π)

$$=\frac{\mathrm{2}}{\pi} \\ $$

Answered by mr W last updated on 30/Nov/21

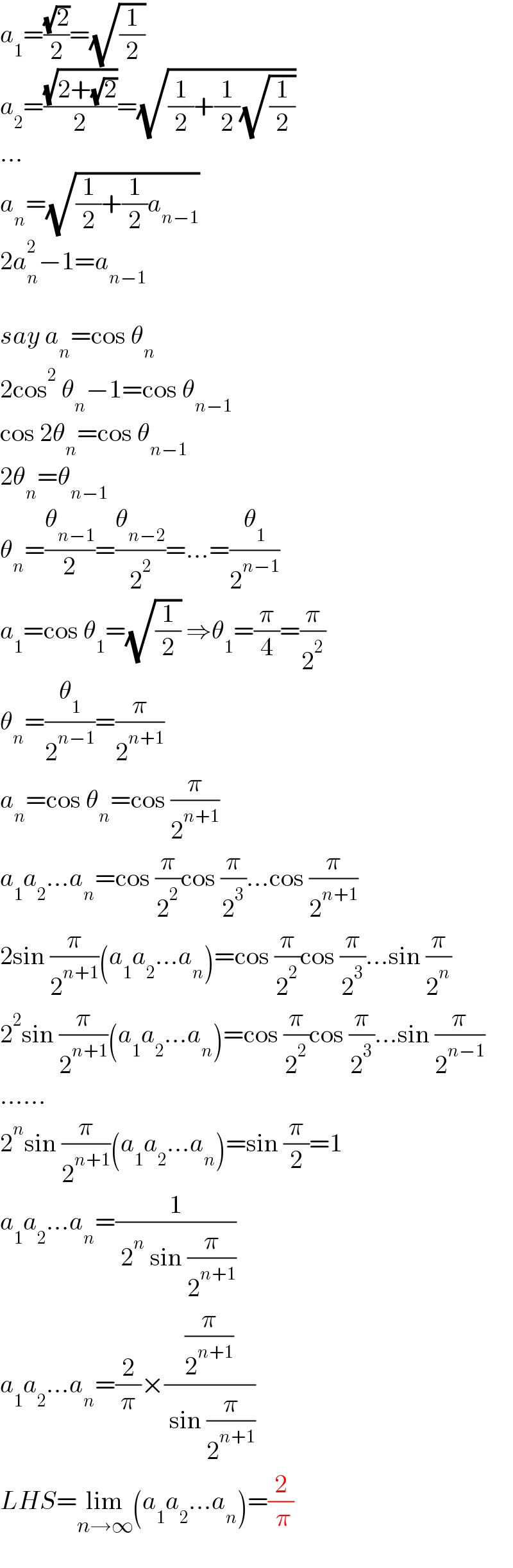
a_1 =((√2)/2)=(√(1/2)) a_2 =((√(2+(√2)))/2)=(√((1/2)+(1/2)(√(1/2)))) ... a_n =(√((1/2)+(1/2)a_(n−1) )) 2a_n ^2 −1=a_(n−1) say a_n =cos θ_n 2cos^2 θ_n −1=cos θ_(n−1) cos 2θ_n =cos θ_(n−1) 2θ_n =θ_(n−1) θ_n =(θ_(n−1) /2)=(θ_(n−2) /2^2 )=...=(θ_1 /2^(n−1) ) a_1 =cos θ_1 =(√(1/2)) ⇒θ_1 =(π/4)=(π/2^2 ) θ_n =(θ_1 /2^(n−1) )=(π/2^(n+1) ) a_n =cos θ_n =cos (π/2^(n+1) ) a_1 a_2 ...a_n =cos (π/2^2 )cos (π/2^3 )...cos (π/2^(n+1) ) 2sin (π/2^(n+1) )(a_1 a_2 ...a_n )=cos (π/2^2 )cos (π/2^3 )...sin (π/2^n ) 2^2 sin (π/2^(n+1) )(a_1 a_2 ...a_n )=cos (π/2^2 )cos (π/2^3 )...sin (π/2^(n−1) ) ...... 2^n sin (π/2^(n+1) )(a_1 a_2 ...a_n )=sin (π/2)=1 a_1 a_2 ...a_n =(1/( 2^n sin (π/2^(n+1) ))) a_1 a_2 ...a_n =(2/π)×((π/2^(n+1) )/( sin (π/2^(n+1) ))) LHS=lim_(n→∞) (a_1 a_2 ...a_n )=(2/( π))

$${a}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${a}_{\mathrm{2}} =\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}} \\ $$$$... \\ $$$${a}_{{n}} =\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{a}_{{n}−\mathrm{1}} } \\ $$$$\mathrm{2}{a}_{{n}} ^{\mathrm{2}} −\mathrm{1}={a}_{{n}−\mathrm{1}} \\ $$$$ \\ $$$${say}\:{a}_{{n}} =\mathrm{cos}\:\theta_{{n}} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \:\theta_{{n}} −\mathrm{1}=\mathrm{cos}\:\theta_{{n}−\mathrm{1}} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta_{{n}} =\mathrm{cos}\:\theta_{{n}−\mathrm{1}} \\ $$$$\mathrm{2}\theta_{{n}} =\theta_{{n}−\mathrm{1}} \\ $$$$\theta_{{n}} =\frac{\theta_{{n}−\mathrm{1}} }{\mathrm{2}}=\frac{\theta_{{n}−\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }=...=\frac{\theta_{\mathrm{1}} }{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} =\mathrm{cos}\:\theta_{\mathrm{1}} =\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}\:\Rightarrow\theta_{\mathrm{1}} =\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}^{\mathrm{2}} } \\ $$$$\theta_{{n}} =\frac{\theta_{\mathrm{1}} }{\mathrm{2}^{{n}−\mathrm{1}} }=\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$${a}_{{n}} =\mathrm{cos}\:\theta_{{n}} =\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} =\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{3}} }...\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$\mathrm{2sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\left({a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} \right)=\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{3}} }...\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{2}^{\mathrm{2}} \mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\left({a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} \right)=\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{3}} }...\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$$...... \\ $$$$\mathrm{2}^{{n}} \mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\left({a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} \right)=\mathrm{sin}\:\frac{\pi}{\mathrm{2}}=\mathrm{1} \\ $$$${a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} =\frac{\mathrm{1}}{\:\mathrm{2}^{{n}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }} \\ $$$${a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} =\frac{\mathrm{2}}{\pi}×\frac{\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}{\:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }} \\ $$$${LHS}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left({a}_{\mathrm{1}} {a}_{\mathrm{2}} ...{a}_{{n}} \right)=\frac{\mathrm{2}}{\:\pi} \\ $$

Commented by HongKing last updated on 29/Nov/21

Perfecy my dear Sir thank you so much

$$\mathrm{Perfecy}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Commented by Tawa11 last updated on 30/Nov/21

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com