
Question Number 161656 by amin96 last updated on 20/Dec/21
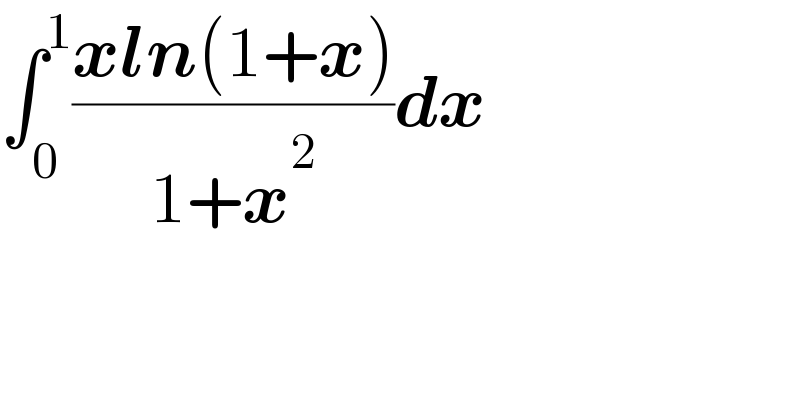
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{xln}}\left(\mathrm{1}+\boldsymbol{{x}}\right)}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}} \\ $$
Commented by Ar Brandon last updated on 21/Dec/21
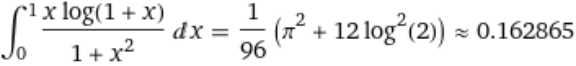
Commented by amin96 last updated on 21/Dec/21

$${solution}??? \\ $$
Commented by smallEinstein last updated on 22/Dec/21

Answered by mindispower last updated on 21/Dec/21
![∫_0 ^1 (x/(1+x^2 ))ln(((1−x)/(1+x)))dx=A y=((1−x)/(1+x))⇒x=((1−y)/(1+y))⇒dx=((−2dy)/((1+y)^2 )) =∫_0 ^1 ((1−y)/(1+y)).((ln(y))/(1+y^2 )).dy =∫_0 ^1 ((ln(y))/(1+y))−((yln(y))/(1+y^2 ))dy=(3/4)∫_0 ^1 ((ln(y))/(1+y))dy =−(3/4)∫_0 ^1 ((ln(1+y))/y)dy=(3/4)(−∫_0 ^1 ((ln(1−(−y)))/((−y)))d(−y)) =(3/4)Li_2 (−1)=(3/4).−(π^2 /(12))=−(π^2 /(16)) ∫_0 ^1 ((xln(1−x^2 ))/(1+x^2 ))=(1/2)∫_0 ^1 ((ln(1−y))/(1+y))dt=B =(1/2)∫_0 ^1 ((ln(t))/(2−t))dt =(1/2)∫_0 ^1 ((ln((t/2))+ln(2))/(1−((t/2))))d((t/2))=(1/2)∫_0 ^(1/2) ((ln(u))/(1−u))du+((ln(2))/2)∫_0 ^(1/2) (du/(1−u)) =−(1/2)∫_0 ^(1/2) ((ln(1−(1−u)))/(1−u))d(1−u) =(1/2)Li_2 (1−u)]_0 ^(1/2) −((ln(2))/2)ln((1/2)) =(1/2)[Li_2 ((1/2))−Li_2 (1)+ln^2 (2)] =(1/2)[(π^2 /(12))−(π^2 /6)+((ln^2 (2))/2)]=−(π^2 /(24))+((ln^2 (2))/4) ∫_0 ^1 (x/(1+x^2 ))ln(1+x)dx=((A+B)/2)=−((5π^2 )/(96))+((ln^2 (2))/8) =](Q161693.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{ln}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right){dx}={A} \\ $$$${y}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\Rightarrow{x}=\frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}\Rightarrow{dx}=\frac{−\mathrm{2}{dy}}{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}.\frac{{ln}\left({y}\right)}{\mathrm{1}+{y}^{\mathrm{2}} }.{dy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({y}\right)}{\mathrm{1}+{y}}−\frac{{yln}\left({y}\right)}{\mathrm{1}+{y}^{\mathrm{2}} }{dy}=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({y}\right)}{\mathrm{1}+{y}}{dy} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{y}\right)}{{y}}{dy}=\frac{\mathrm{3}}{\mathrm{4}}\left(−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−\left(−{y}\right)\right)}{\left(−{y}\right)}{d}\left(−{y}\right)\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)=\frac{\mathrm{3}}{\mathrm{4}}.−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{xln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{y}\right)}{\mathrm{1}+{y}}{dt}={B} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({t}\right)}{\mathrm{2}−{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\frac{{t}}{\mathrm{2}}\right)+{ln}\left(\mathrm{2}\right)}{\mathrm{1}−\left(\frac{{t}}{\mathrm{2}}\right)}{d}\left(\frac{{t}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}\left({u}\right)}{\mathrm{1}−{u}}{du}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{du}}{\mathrm{1}−{u}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}\left(\mathrm{1}−\left(\mathrm{1}−{u}\right)\right)}{\mathrm{1}−{u}}{d}\left(\mathrm{1}−{u}\right) \\ $$$$\left.=\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(\mathrm{1}−{u}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} −\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{Li}_{\mathrm{2}} \left(\mathrm{1}\right)+{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}\right]=−\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{ln}\left(\mathrm{1}+{x}\right){dx}=\frac{{A}+{B}}{\mathrm{2}}=−\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{96}}+\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$= \\ $$$$ \\ $$
Commented by smallEinstein last updated on 21/Dec/21
pls recheck solution
