Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 162305 by mathlove last updated on 28/Dec/21

proof that 2^(n+1) >(n+2)sin n

$${proof}\:{that} \\ $$ $$\mathrm{2}^{{n}+\mathrm{1}} >\left({n}+\mathrm{2}\right)\mathrm{sin}\:{n} \\ $$

Answered by aleks041103 last updated on 28/Dec/21

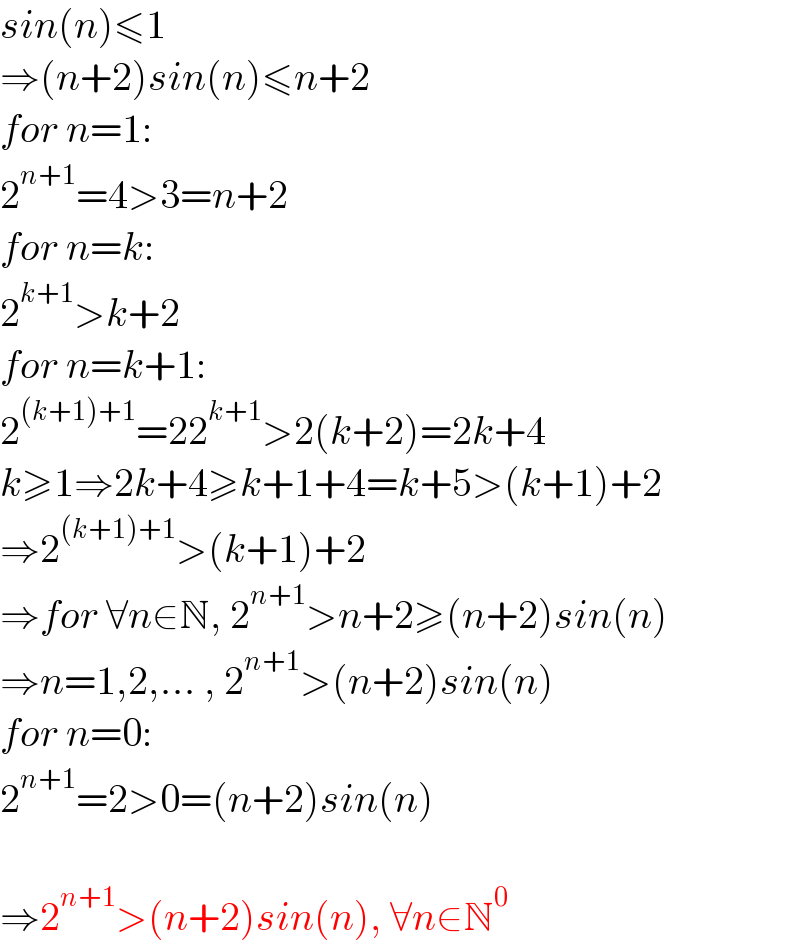
sin(n)≤1 ⇒(n+2)sin(n)≤n+2 for n=1: 2^(n+1) =4>3=n+2 for n=k: 2^(k+1) >k+2 for n=k+1: 2^((k+1)+1) =22^(k+1) >2(k+2)=2k+4 k≥1⇒2k+4≥k+1+4=k+5>(k+1)+2 ⇒2^((k+1)+1) >(k+1)+2 ⇒for ∀n∈N, 2^(n+1) >n+2≥(n+2)sin(n) ⇒n=1,2,... , 2^(n+1) >(n+2)sin(n) for n=0: 2^(n+1) =2>0=(n+2)sin(n) ⇒2^(n+1) >(n+2)sin(n), ∀n∈N^0

$${sin}\left({n}\right)\leqslant\mathrm{1} \\ $$ $$\Rightarrow\left({n}+\mathrm{2}\right){sin}\left({n}\right)\leqslant{n}+\mathrm{2} \\ $$ $${for}\:{n}=\mathrm{1}: \\ $$ $$\mathrm{2}^{{n}+\mathrm{1}} =\mathrm{4}>\mathrm{3}={n}+\mathrm{2} \\ $$ $${for}\:{n}={k}: \\ $$ $$\mathrm{2}^{{k}+\mathrm{1}} >{k}+\mathrm{2} \\ $$ $${for}\:{n}={k}+\mathrm{1}: \\ $$ $$\mathrm{2}^{\left({k}+\mathrm{1}\right)+\mathrm{1}} =\mathrm{22}^{{k}+\mathrm{1}} >\mathrm{2}\left({k}+\mathrm{2}\right)=\mathrm{2}{k}+\mathrm{4} \\ $$ $${k}\geqslant\mathrm{1}\Rightarrow\mathrm{2}{k}+\mathrm{4}\geqslant{k}+\mathrm{1}+\mathrm{4}={k}+\mathrm{5}>\left({k}+\mathrm{1}\right)+\mathrm{2} \\ $$ $$\Rightarrow\mathrm{2}^{\left({k}+\mathrm{1}\right)+\mathrm{1}} >\left({k}+\mathrm{1}\right)+\mathrm{2} \\ $$ $$\Rightarrow{for}\:\forall{n}\in\mathbb{N},\:\mathrm{2}^{{n}+\mathrm{1}} >{n}+\mathrm{2}\geqslant\left({n}+\mathrm{2}\right){sin}\left({n}\right) \\ $$ $$\Rightarrow{n}=\mathrm{1},\mathrm{2},...\:,\:\mathrm{2}^{{n}+\mathrm{1}} >\left({n}+\mathrm{2}\right){sin}\left({n}\right) \\ $$ $${for}\:{n}=\mathrm{0}: \\ $$ $$\mathrm{2}^{{n}+\mathrm{1}} =\mathrm{2}>\mathrm{0}=\left({n}+\mathrm{2}\right){sin}\left({n}\right) \\ $$ $$ \\ $$ $$\Rightarrow\mathrm{2}^{{n}+\mathrm{1}} >\left({n}+\mathrm{2}\right){sin}\left({n}\right),\:\forall{n}\in\mathbb{N}^{\mathrm{0}} \\ $$

Answered by mr W last updated on 28/Dec/21

recall: 1≥sin n for any n∈R (1+a)^n >1+na for a>0 2^(n+1) =(1+1)^(n+1) >1+(n+1)×1=n+2=(n+2)×1 ≥(n+2) sin n ⇒ 2^(n+1) >(n+2) sin n ✓

$${recall}: \\ $$ $$\mathrm{1}\geqslant\mathrm{sin}\:{n}\:{for}\:{any}\:{n}\in\mathbb{R} \\ $$ $$\left(\mathrm{1}+{a}\right)^{{n}} >\mathrm{1}+{na}\:{for}\:{a}>\mathrm{0} \\ $$ $$ \\ $$ $$\mathrm{2}^{{n}+\mathrm{1}} =\left(\mathrm{1}+\mathrm{1}\right)^{{n}+\mathrm{1}} \\ $$ $$\:\:\:\:\:\:\:\:\:>\mathrm{1}+\left({n}+\mathrm{1}\right)×\mathrm{1}={n}+\mathrm{2}=\left({n}+\mathrm{2}\right)×\mathrm{1} \\ $$ $$\:\:\:\:\:\:\:\:\:\geqslant\left({n}+\mathrm{2}\right)\:\mathrm{sin}\:{n} \\ $$ $$\Rightarrow\:\mathrm{2}^{{n}+\mathrm{1}} >\left({n}+\mathrm{2}\right)\:\mathrm{sin}\:{n}\:\checkmark \\ $$

Commented byaleks041103 last updated on 28/Dec/21

It is worth noting that (n+2)≥(n+2)sin(n) is true for n≥−2

$${It}\:{is}\:{worth}\:{noting}\:{that} \\ $$ $$\left({n}+\mathrm{2}\right)\geqslant\left({n}+\mathrm{2}\right){sin}\left({n}\right) \\ $$ $${is}\:{true}\:{for}\:{n}\geqslant−\mathrm{2} \\ $$

Commented bymr W last updated on 29/Dec/21

i assumed n∈N what the questioner also meant, i think. if n∈Z, then 2^(n+1) >(n+2) sin n is true for n≥−6.

$${i}\:{assumed}\:{n}\in\mathbb{N}\:{what}\:{the}\:{questioner} \\ $$ $${also}\:{meant},\:{i}\:{think}. \\ $$ $${if}\:{n}\in\mathbb{Z},\:{then}\:\mathrm{2}^{{n}+\mathrm{1}} >\left({n}+\mathrm{2}\right)\:\mathrm{sin}\:{n}\:{is} \\ $$ $${true}\:{for}\:{n}\geqslant−\mathrm{6}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com