
Question Number 162584 by SANOGO last updated on 30/Dec/21
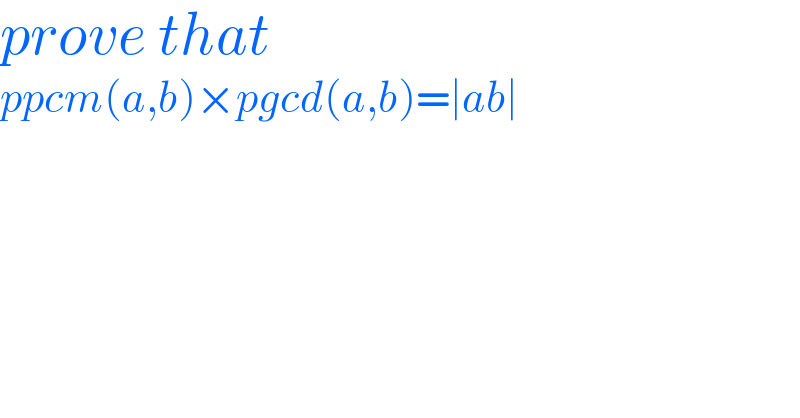
$${prove}\:{that} \\ $$$${ppcm}\left({a},{b}\right)×{pgcd}\left({a},{b}\right)=\mid{ab}\mid \\ $$
Answered by mr W last updated on 30/Dec/21
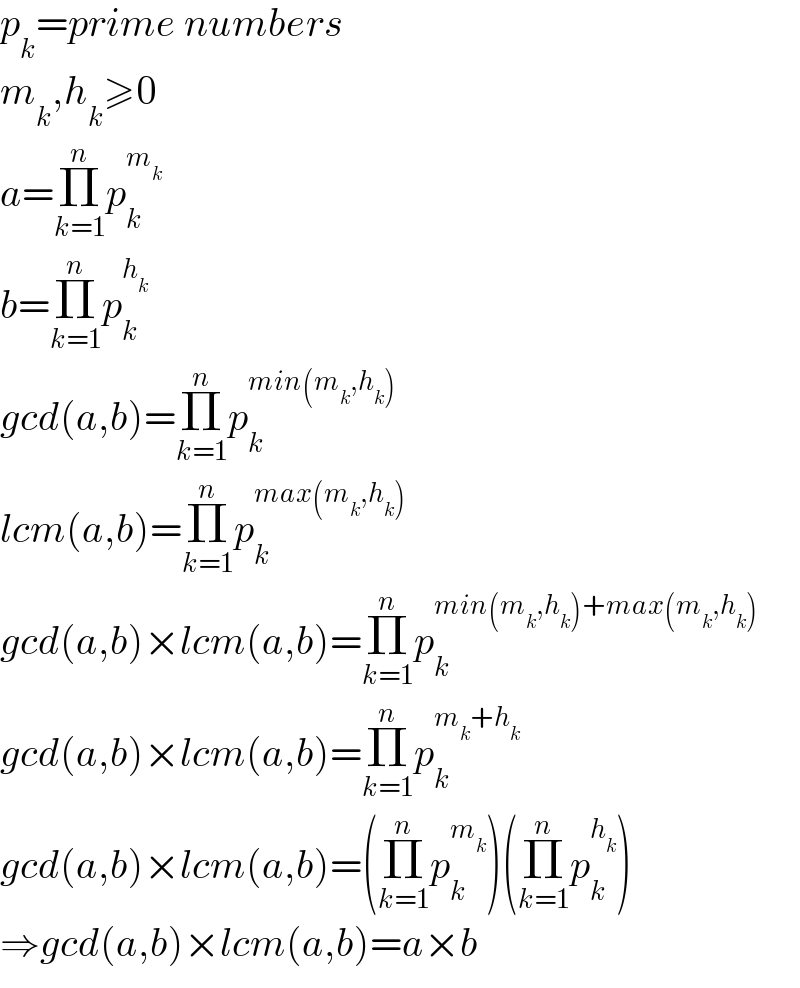
$${p}_{{k}} ={prime}\:{numbers} \\ $$$${m}_{{k}} ,{h}_{{k}} \geqslant\mathrm{0} \\ $$$${a}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{k}} ^{{m}_{{k}} } \\ $$$${b}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{k}} ^{{h}_{{k}} } \\ $$$${gcd}\left({a},{b}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{k}} ^{{min}\left({m}_{{k}} ,{h}_{{k}} \right)} \\ $$$${lcm}\left({a},{b}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{k}} ^{{max}\left({m}_{{k}} ,{h}_{{k}} \right)} \\ $$$${gcd}\left({a},{b}\right)×{lcm}\left({a},{b}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{k}} ^{{min}\left({m}_{{k}} ,{h}_{{k}} \right)+{max}\left({m}_{{k}} ,{h}_{{k}} \right)} \\ $$$${gcd}\left({a},{b}\right)×{lcm}\left({a},{b}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{k}} ^{{m}_{{k}} +{h}_{{k}} } \\ $$$${gcd}\left({a},{b}\right)×{lcm}\left({a},{b}\right)=\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{k}} ^{{m}_{{k}} } \right)\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{k}} ^{{h}_{{k}} } \right) \\ $$$$\Rightarrow{gcd}\left({a},{b}\right)×{lcm}\left({a},{b}\right)={a}×{b} \\ $$
Commented by SANOGO last updated on 30/Dec/21
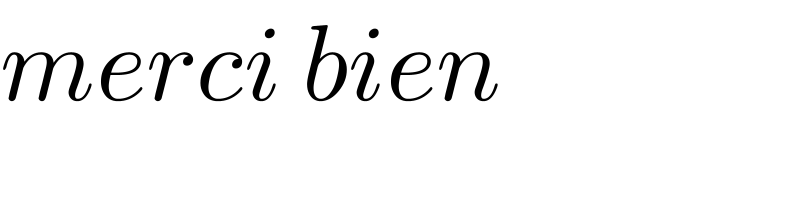
$${merci}\:{bien} \\ $$
Commented by Rasheed.Sindhi last updated on 31/Dec/21

$$\mathbb{G}_{\mathrm{Sir}!} ^{\mathrm{rea}} \mathbb{T} \\ $$
