
Question Number 162877 by HongKing last updated on 01/Jan/22
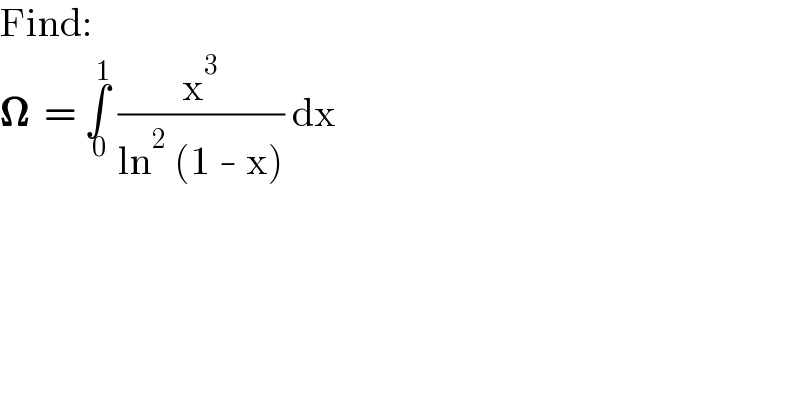
$$\mathrm{Find}: \\ $$$$\boldsymbol{\Omega}\:\:=\:\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{ln}^{\mathrm{2}} \:\left(\mathrm{1}\:-\:\mathrm{x}\right)}\:\mathrm{dx} \\ $$
Answered by Ar Brandon last updated on 02/Jan/22
![Ω=∫_0 ^1 (x^3 /(ln^2 (1−x)))dx=∫_0 ^1 (((1−x)^3 )/(ln^2 x))dx f(α)=∫_0 ^1 ((x^α (1−x)^3 )/(ln^2 x))dx⇒f^((2)) (α)=∫_0 ^1 x^α (1−x)^3 dx =β(α+1, 4)=((6Γ(α+1))/(Γ(α+5)))=(6/((α+4)(α+3)(α+2)(α+1))) =−(1/(α+4))+(3/(α+3))−(3/(α+2))+(1/(α+1)) f^((1)) (α)=−ln(α+4)+3ln(α+3)−3ln(α+2)+ln(α+1) f(α)=−(α+4)[ln(α+4)−1]+3(α+3)[ln(α+3)−1] −3(α+2)[ln(α+2)−1]+(α+1)[ln(α+1)−1] f(0)=−4(ln4−1)+9(ln3−1)−6(ln2−1)−1 =ln((3^9 /(2^8 ×2^6 )))=∫_0 ^1 (x^3 /(ln^2 (1−x)))dx](Q162905.png)
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} }{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{\mathrm{ln}^{\mathrm{2}} {x}}{dx} \\ $$$${f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\alpha} \left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{\mathrm{ln}^{\mathrm{2}} {x}}{dx}\Rightarrow{f}^{\left(\mathrm{2}\right)} \left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\alpha} \left(\mathrm{1}−{x}\right)^{\mathrm{3}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\beta\left(\alpha+\mathrm{1},\:\mathrm{4}\right)=\frac{\mathrm{6}\Gamma\left(\alpha+\mathrm{1}\right)}{\Gamma\left(\alpha+\mathrm{5}\right)}=\frac{\mathrm{6}}{\left(\alpha+\mathrm{4}\right)\left(\alpha+\mathrm{3}\right)\left(\alpha+\mathrm{2}\right)\left(\alpha+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\alpha+\mathrm{4}}+\frac{\mathrm{3}}{\alpha+\mathrm{3}}−\frac{\mathrm{3}}{\alpha+\mathrm{2}}+\frac{\mathrm{1}}{\alpha+\mathrm{1}} \\ $$$${f}^{\left(\mathrm{1}\right)} \left(\alpha\right)=−\mathrm{ln}\left(\alpha+\mathrm{4}\right)+\mathrm{3ln}\left(\alpha+\mathrm{3}\right)−\mathrm{3ln}\left(\alpha+\mathrm{2}\right)+\mathrm{ln}\left(\alpha+\mathrm{1}\right) \\ $$$${f}\left(\alpha\right)=−\left(\alpha+\mathrm{4}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{4}\right)−\mathrm{1}\right]+\mathrm{3}\left(\alpha+\mathrm{3}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{3}\right)−\mathrm{1}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}\left(\alpha+\mathrm{2}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{2}\right)−\mathrm{1}\right]+\left(\alpha+\mathrm{1}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{1}\right)−\mathrm{1}\right] \\ $$$${f}\left(\mathrm{0}\right)=−\mathrm{4}\left(\mathrm{ln4}−\mathrm{1}\right)+\mathrm{9}\left(\mathrm{ln3}−\mathrm{1}\right)−\mathrm{6}\left(\mathrm{ln2}−\mathrm{1}\right)−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{ln}\left(\frac{\mathrm{3}^{\mathrm{9}} }{\mathrm{2}^{\mathrm{8}} ×\mathrm{2}^{\mathrm{6}} }\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} }{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{dx} \\ $$
Commented by Lordose last updated on 02/Jan/22
After calculating F⁽²⁾(a), when integrating the result, There's supposed to be a constant, i. e ∫F⁽²⁾(a)da = F'(a) + C ∫F'(a) + C = F(a) + aC + D where C and D are constants
Commented by Ar Brandon last updated on 02/Jan/22
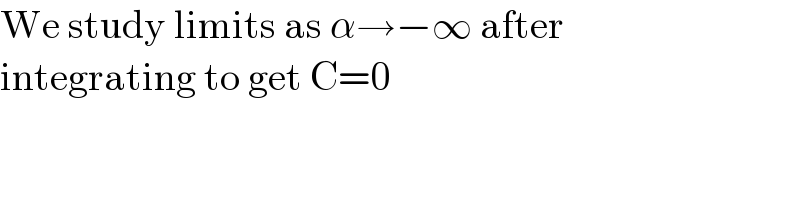
$$\mathrm{We}\:\mathrm{study}\:\mathrm{limits}\:\mathrm{as}\:\alpha\rightarrow−\infty\:\mathrm{after}\: \\ $$$$\mathrm{integrating}\:\mathrm{to}\:\mathrm{get}\:\mathrm{C}=\mathrm{0} \\ $$
Commented by Ar Brandon last updated on 02/Jan/22
![f^((1)) (α)=∫_0 ^1 ((x^α (1−x)^3 )/(lnx))dx =−ln(α+4)+3ln(α+3)−3ln(α+2)+ln(α+1)+C lim_(α→−∞) f^((1)) (α)=0=lim_(α→−∞) ln((((α+3)^3 (α+1))/((α+4)(α+2)^3 )))+C =lim_(α→−∞) ln((((1+(3/α))^3 (1+(1/α)))/((1+(4/α))(1+(2/α))^3 )))+C=ln(1)+C=0⇒C=0 f^((2)) (α)=∫_0 ^1 ((x^α (1−x)^3 )/(ln^2 x))dx =−(α+4)[ln(α+4)−1]+3(α+3)[ln(α+3)−1] −3(α+2)[ln(α+2)−1]+(α+1)[ln(α+1)−1]+D lim_(α→−∞) f(α)=0 =lim_(α→−∞) ln((((α+3)^9 (α+1))/((α+4)^4 (α+2)^6 )))−αln(α+4)+3αln(α+3) −3αln(α+2)+αln(α+1)+D =D=0](Q162915.png)
$${f}^{\left(\mathrm{1}\right)} \left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\alpha} \left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{\mathrm{ln}{x}}{dx} \\ $$$$=−\mathrm{ln}\left(\alpha+\mathrm{4}\right)+\mathrm{3ln}\left(\alpha+\mathrm{3}\right)−\mathrm{3ln}\left(\alpha+\mathrm{2}\right)+\mathrm{ln}\left(\alpha+\mathrm{1}\right)+{C} \\ $$$$\underset{\alpha\rightarrow−\infty} {\mathrm{lim}}{f}^{\left(\mathrm{1}\right)} \left(\alpha\right)=\mathrm{0}=\underset{\alpha\rightarrow−\infty} {\mathrm{lim}ln}\left(\frac{\left(\alpha+\mathrm{3}\right)^{\mathrm{3}} \left(\alpha+\mathrm{1}\right)}{\left(\alpha+\mathrm{4}\right)\left(\alpha+\mathrm{2}\right)^{\mathrm{3}} }\right)+\mathrm{C} \\ $$$$=\underset{\alpha\rightarrow−\infty} {\mathrm{lim}ln}\left(\frac{\left(\mathrm{1}+\frac{\mathrm{3}}{\alpha}\right)^{\mathrm{3}} \left(\mathrm{1}+\frac{\mathrm{1}}{\alpha}\right)}{\left(\mathrm{1}+\frac{\mathrm{4}}{\alpha}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{\alpha}\right)^{\mathrm{3}} }\right)+\mathrm{C}=\mathrm{ln}\left(\mathrm{1}\right)+\mathrm{C}=\mathrm{0}\Rightarrow\mathrm{C}=\mathrm{0} \\ $$$${f}^{\left(\mathrm{2}\right)} \left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\alpha} \left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{\mathrm{ln}^{\mathrm{2}} {x}}{dx} \\ $$$$=−\left(\alpha+\mathrm{4}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{4}\right)−\mathrm{1}\right]+\mathrm{3}\left(\alpha+\mathrm{3}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{3}\right)−\mathrm{1}\right] \\ $$$$\:\:\:\:−\mathrm{3}\left(\alpha+\mathrm{2}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{2}\right)−\mathrm{1}\right]+\left(\alpha+\mathrm{1}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{1}\right)−\mathrm{1}\right]+\mathrm{D} \\ $$$$\underset{\alpha\rightarrow−\infty} {\mathrm{lim}}{f}\left(\alpha\right)=\mathrm{0} \\ $$$$=\underset{\alpha\rightarrow−\infty} {\mathrm{lim}ln}\left(\frac{\left(\alpha+\mathrm{3}\right)^{\mathrm{9}} \left(\alpha+\mathrm{1}\right)}{\left(\alpha+\mathrm{4}\right)^{\mathrm{4}} \left(\alpha+\mathrm{2}\right)^{\mathrm{6}} }\right)−\alpha\mathrm{ln}\left(\alpha+\mathrm{4}\right)+\mathrm{3}\alpha\mathrm{ln}\left(\alpha+\mathrm{3}\right) \\ $$$$\:\:\:\:−\mathrm{3}\alpha\mathrm{ln}\left(\alpha+\mathrm{2}\right)+\alpha\mathrm{ln}\left(\alpha+\mathrm{1}\right)+\mathrm{D} \\ $$$$=\mathrm{D}=\mathrm{0} \\ $$
Commented by Lordose last updated on 02/Jan/22
Nice one Bro.
Commented by Ar Brandon last updated on 02/Jan/22
Thanks bro. You too made a good remark there.
Commented by HongKing last updated on 02/Jan/22
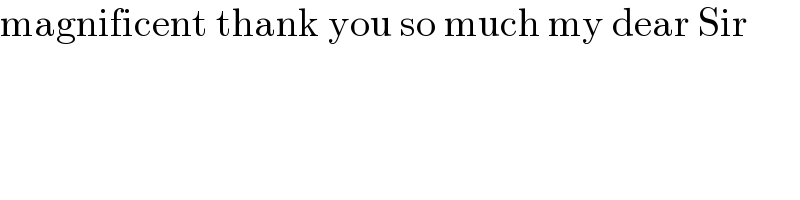
$$\mathrm{magnificent}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
Answered by Ar Brandon last updated on 02/Jan/22
![Ω=∫_0 ^1 (x^3 /(ln^2 (1−x)))dx=∫_0 ^1 (((1−x)^3 )/(ln^2 x))dx x=e^(−t) ⇒dx=−e^(−t) dt =∫_0 ^∞ (((1−e^(−t) )^3 )/t^2 )∙e^(−t) dt=∫_0 ^∞ ((e^(−t) /t^2 )−3(e^(−2t) /t^2 )+3(e^(−3t) /t^2 )−(e^(−4t) /t^2 ))dt =∫_0 ^∞ ((t/(1+t))−((3t)/(2+t))+((3t)/(3+t))−(t/(4+t)))dt , maz identity =∫_0 ^∞ (1−(1/(1+t))−3+(6/(2+t))+3−(9/(3+t))−1+(4/(4+t)))dt =[ln(1+t)+6ln(2+t)−9ln(3+t)+4ln(4+t)]_0 ^∞ =[ln((((1+t)(2+t)^6 (4+t)^4 )/((3+t)^9 )))]_0 ^∞ =ln(1)−ln(((2^6 ×4^4 )/3^9 )) =−ln(((2^6 ×2^8 )/3^9 ))=ln((3^9 /(2^8 ×2^6 )))](Q162923.png)
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} }{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{\mathrm{ln}^{\mathrm{2}} {x}}{dx}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}={e}^{−{t}} \Rightarrow{dx}=−{e}^{−{t}} {dt} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{1}−{e}^{−{t}} \right)^{\mathrm{3}} }{{t}^{\mathrm{2}} }\centerdot{e}^{−{t}} {dt}=\int_{\mathrm{0}} ^{\infty} \left(\frac{{e}^{−{t}} }{{t}^{\mathrm{2}} }−\mathrm{3}\frac{{e}^{−\mathrm{2}{t}} }{{t}^{\mathrm{2}} }+\mathrm{3}\frac{{e}^{−\mathrm{3}{t}} }{{t}^{\mathrm{2}} }−\frac{{e}^{−\mathrm{4}{t}} }{{t}^{\mathrm{2}} }\right){dt} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\infty} \left(\frac{{t}}{\mathrm{1}+{t}}−\frac{\mathrm{3}{t}}{\mathrm{2}+{t}}+\frac{\mathrm{3}{t}}{\mathrm{3}+{t}}−\frac{{t}}{\mathrm{4}+{t}}\right){dt}\:,\:\mathrm{maz}\:\mathrm{identity} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}−\mathrm{3}+\frac{\mathrm{6}}{\mathrm{2}+{t}}+\mathrm{3}−\frac{\mathrm{9}}{\mathrm{3}+{t}}−\mathrm{1}+\frac{\mathrm{4}}{\mathrm{4}+{t}}\right){dt} \\ $$$$\:\:\:\:=\left[\mathrm{ln}\left(\mathrm{1}+{t}\right)+\mathrm{6ln}\left(\mathrm{2}+{t}\right)−\mathrm{9ln}\left(\mathrm{3}+{t}\right)+\mathrm{4ln}\left(\mathrm{4}+{t}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:\:=\left[\mathrm{ln}\left(\frac{\left(\mathrm{1}+{t}\right)\left(\mathrm{2}+{t}\right)^{\mathrm{6}} \left(\mathrm{4}+{t}\right)^{\mathrm{4}} }{\left(\mathrm{3}+{t}\right)^{\mathrm{9}} }\right)\right]_{\mathrm{0}} ^{\infty} =\mathrm{ln}\left(\mathrm{1}\right)−\mathrm{ln}\left(\frac{\mathrm{2}^{\mathrm{6}} ×\mathrm{4}^{\mathrm{4}} }{\mathrm{3}^{\mathrm{9}} }\right) \\ $$$$\:\:\:\:=−\mathrm{ln}\left(\frac{\mathrm{2}^{\mathrm{6}} ×\mathrm{2}^{\mathrm{8}} }{\mathrm{3}^{\mathrm{9}} }\right)=\mathrm{ln}\left(\frac{\mathrm{3}^{\mathrm{9}} }{\mathrm{2}^{\mathrm{8}} ×\mathrm{2}^{\mathrm{6}} }\right) \\ $$
Commented by Lordose last updated on 02/Jan/22
Exactly what i used��
Commented by Ar Brandon last updated on 02/Jan/22
I stole the method from you this morning ��
Commented by Lordose last updated on 03/Jan/22
����
