
Question Number 163168 by kdaramaths last updated on 04/Jan/22

Commented by mr W last updated on 04/Jan/22
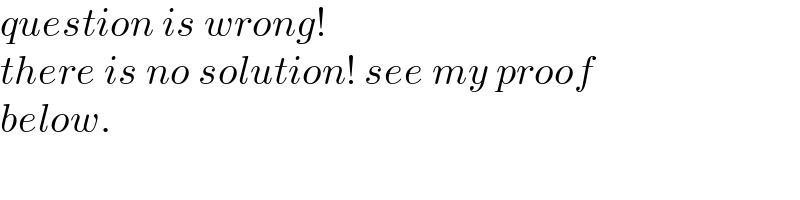
$${question}\:{is}\:{wrong}! \\ $$$${there}\:{is}\:{no}\:{solution}!\:{see}\:{my}\:{proof} \\ $$$${below}. \\ $$
Answered by mahdipoor last updated on 04/Jan/22
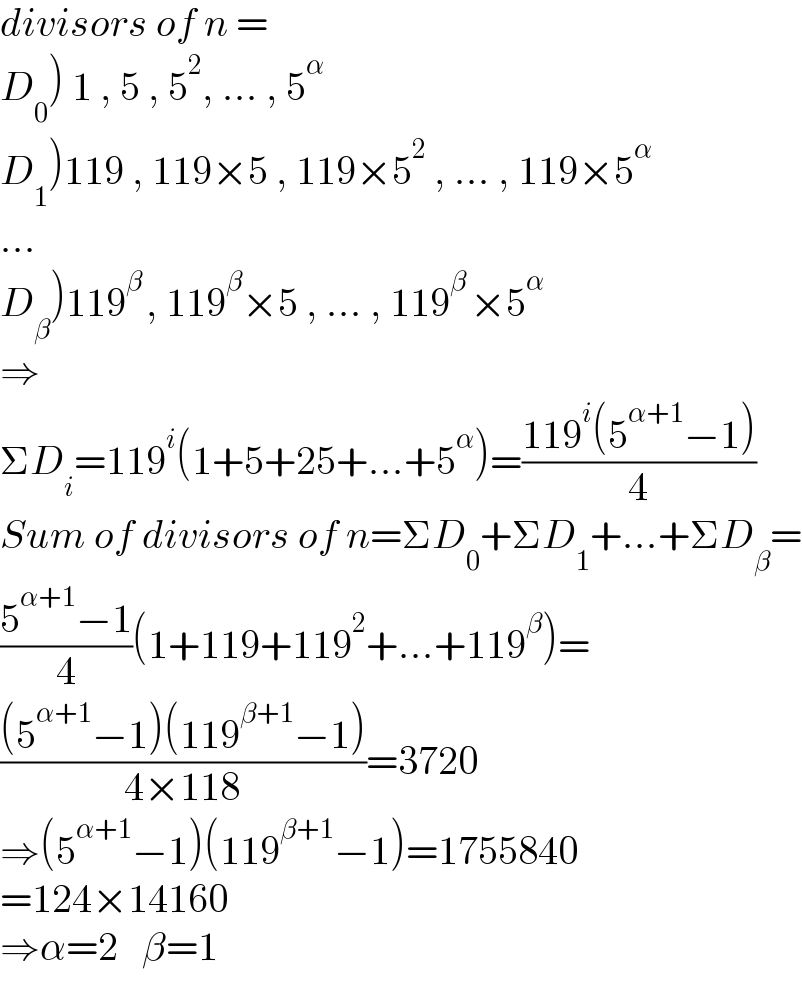
$${divisors}\:{of}\:{n}\:= \\ $$$$\left.{D}_{\mathrm{0}} \right)\:\mathrm{1}\:,\:\mathrm{5}\:,\:\mathrm{5}^{\mathrm{2}} ,\:...\:,\:\mathrm{5}^{\alpha\:} \: \\ $$$$\left.{D}_{\mathrm{1}} \right)\mathrm{119}\:,\:\mathrm{119}×\mathrm{5}\:,\:\mathrm{119}×\mathrm{5}^{\mathrm{2}} \:,\:...\:,\:\mathrm{119}×\mathrm{5}^{\alpha\:} \\ $$$$... \\ $$$$\left.{D}_{\beta} \right)\mathrm{119}^{\beta\:} ,\:\mathrm{119}^{\beta} ×\mathrm{5}\:,\:...\:,\:\mathrm{119}^{\beta\:} ×\mathrm{5}^{\alpha} \\ $$$$\Rightarrow \\ $$$$\Sigma{D}_{{i}} =\mathrm{119}^{{i}} \left(\mathrm{1}+\mathrm{5}+\mathrm{25}+...+\mathrm{5}^{\alpha} \right)=\frac{\mathrm{119}^{{i}} \left(\mathrm{5}^{\alpha+\mathrm{1}} −\mathrm{1}\right)}{\mathrm{4}} \\ $$$${Sum}\:{of}\:{divisors}\:{of}\:{n}=\Sigma{D}_{\mathrm{0}} +\Sigma{D}_{\mathrm{1}} +...+\Sigma{D}_{\beta} = \\ $$$$\frac{\mathrm{5}^{\alpha+\mathrm{1}} −\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{119}+\mathrm{119}^{\mathrm{2}} +...+\mathrm{119}^{\beta} \right)= \\ $$$$\frac{\left(\mathrm{5}^{\alpha+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{119}^{\beta+\mathrm{1}} −\mathrm{1}\right)}{\mathrm{4}×\mathrm{118}}=\mathrm{3720} \\ $$$$\Rightarrow\left(\mathrm{5}^{\alpha+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{119}^{\beta+\mathrm{1}} −\mathrm{1}\right)=\mathrm{1755840} \\ $$$$=\mathrm{124}×\mathrm{14160} \\ $$$$\Rightarrow\alpha=\mathrm{2}\:\:\:\beta=\mathrm{1} \\ $$
Commented by mr W last updated on 04/Jan/22
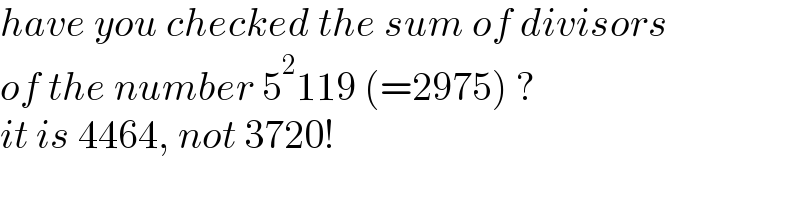
$${have}\:{you}\:{checked}\:{the}\:{sum}\:{of}\:{divisors} \\ $$$${of}\:{the}\:{number}\:\mathrm{5}^{\mathrm{2}} \mathrm{119}\:\left(=\mathrm{2975}\right)\:? \\ $$$${it}\:{is}\:\mathrm{4464},\:{not}\:\mathrm{3720}! \\ $$
Commented by kdaramaths last updated on 04/Jan/22
thanks
Commented by mr W last updated on 04/Jan/22

Commented by mahdipoor last updated on 04/Jan/22
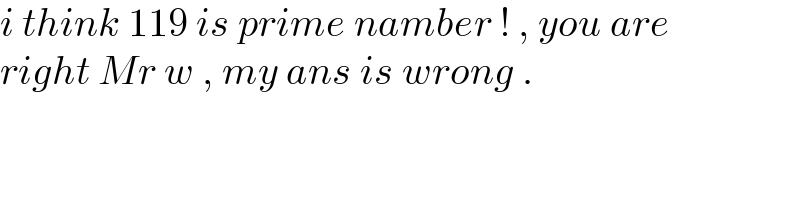
$${i}\:{think}\:\mathrm{119}\:{is}\:{prime}\:{namber}\:!\:,\:{you}\:{are}\: \\ $$$${right}\:{Mr}\:{w}\:,\:{my}\:{ans}\:{is}\:{wrong}\:. \\ $$
Commented by mr W last updated on 05/Jan/22

$${your}\:{method}\:{is}\:{correct}. \\ $$$${maybe}\:{the}\:{person}\:{who}\:{wrote}\:{the}\: \\ $$$${question}\:{also}\:{thinks}\:{that}\:\mathrm{119}\:{is}\:{a} \\ $$$${prime}\:{number},\:{because}\:{he}\:{expected} \\ $$$${exactly}\:{that}\:{what}\:{you}\:{did}. \\ $$
Answered by mr W last updated on 04/Jan/22
![n=5^α 119^β =5^α 7^β 17^β α,β≥1 S=Σ_(p=0) ^α Σ_(q=0) ^β Σ_(r=0) ^β 5^p 7^q 17^r S=((5^(α+1) −1)/(5−1))×((7^(β+1) −1)/(7−1))×((17^(β+1) −1)/(17−1)) S=(((5^(α+1) −1)(7^(β+1) −1)(17^(β+1) −1))/(384))=3720 so the question is to find α, β ∈N, such that (5^(α+1) −1)(7^(β+1) −1)(17^(β+1) −1)=3720×384 5^(α+1) −1<((3720×384)/((7^2 −1)(17^2 −1))) α<log_5 [((3720×384)/((7^2 −1)(17^2 −1)))+1]−1≈1.88 ⇒α=1 (7^(β+1) −1)(17^(β+1) −1)<((3720×384)/((5^2 −1)))=59520 ⇒β<1.31 ⇒β=1 but with α=1, β=1: S=(((5^2 −1)(7^2 −1)(17^2 −1))/(384))=864<3720 with α=2, β=1: S=(((5^3 −1)(7^2 −1)(17^2 −1))/(384))=4464>3720 with α=1, β=2: S=(((5^2 −1)(7^3 −1)(17^3 −1))/(384))=104994>3720 ⇒there exist no α,β such that the sum of divisors of 5^α 119^β is 3720!](Q163186.png)
$${n}=\mathrm{5}^{\alpha} \mathrm{119}^{\beta} =\mathrm{5}^{\alpha} \mathrm{7}^{\beta} \mathrm{17}^{\beta} \\ $$$$\alpha,\beta\geqslant\mathrm{1} \\ $$$${S}=\underset{{p}=\mathrm{0}} {\overset{\alpha} {\sum}}\underset{{q}=\mathrm{0}} {\overset{\beta} {\sum}}\underset{{r}=\mathrm{0}} {\overset{\beta} {\sum}}\mathrm{5}^{{p}} \mathrm{7}^{{q}} \mathrm{17}^{{r}} \\ $$$${S}=\frac{\mathrm{5}^{\alpha+\mathrm{1}} −\mathrm{1}}{\mathrm{5}−\mathrm{1}}×\frac{\mathrm{7}^{\beta+\mathrm{1}} −\mathrm{1}}{\mathrm{7}−\mathrm{1}}×\frac{\mathrm{17}^{\beta+\mathrm{1}} −\mathrm{1}}{\mathrm{17}−\mathrm{1}} \\ $$$${S}=\frac{\left(\mathrm{5}^{\alpha+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{7}^{\beta+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{17}^{\beta+\mathrm{1}} −\mathrm{1}\right)}{\mathrm{384}}=\mathrm{3720} \\ $$$${so}\:{the}\:{question}\:{is}\:{to}\:{find}\:\alpha,\:\beta\:\in\mathbb{N}, \\ $$$${such}\:{that} \\ $$$$\left(\mathrm{5}^{\alpha+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{7}^{\beta+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{17}^{\beta+\mathrm{1}} −\mathrm{1}\right)=\mathrm{3720}×\mathrm{384} \\ $$$$ \\ $$$$\mathrm{5}^{\alpha+\mathrm{1}} −\mathrm{1}<\frac{\mathrm{3720}×\mathrm{384}}{\left(\mathrm{7}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{17}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\alpha<\mathrm{log}_{\mathrm{5}} \:\left[\frac{\mathrm{3720}×\mathrm{384}}{\left(\mathrm{7}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{17}^{\mathrm{2}} −\mathrm{1}\right)}+\mathrm{1}\right]−\mathrm{1}\approx\mathrm{1}.\mathrm{88} \\ $$$$\Rightarrow\alpha=\mathrm{1} \\ $$$$\left(\mathrm{7}^{\beta+\mathrm{1}} −\mathrm{1}\right)\left(\mathrm{17}^{\beta+\mathrm{1}} −\mathrm{1}\right)<\frac{\mathrm{3720}×\mathrm{384}}{\left(\mathrm{5}^{\mathrm{2}} −\mathrm{1}\right)}=\mathrm{59520} \\ $$$$\Rightarrow\beta<\mathrm{1}.\mathrm{31}\: \\ $$$$\Rightarrow\beta=\mathrm{1} \\ $$$$ \\ $$$${but}\:{with}\:\alpha=\mathrm{1},\:\beta=\mathrm{1}: \\ $$$${S}=\frac{\left(\mathrm{5}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{7}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{17}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{384}}=\mathrm{864}<\mathrm{3720} \\ $$$${with}\:\alpha=\mathrm{2},\:\beta=\mathrm{1}: \\ $$$${S}=\frac{\left(\mathrm{5}^{\mathrm{3}} −\mathrm{1}\right)\left(\mathrm{7}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{17}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{384}}=\mathrm{4464}>\mathrm{3720} \\ $$$${with}\:\alpha=\mathrm{1},\:\beta=\mathrm{2}: \\ $$$${S}=\frac{\left(\mathrm{5}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{7}^{\mathrm{3}} −\mathrm{1}\right)\left(\mathrm{17}^{\mathrm{3}} −\mathrm{1}\right)}{\mathrm{384}}=\mathrm{104994}>\mathrm{3720} \\ $$$$\Rightarrow{there}\:{exist}\:{no}\:\alpha,\beta\:{such}\:{that} \\ $$$${the}\:{sum}\:{of}\:{divisors}\:{of}\:\mathrm{5}^{\alpha} \mathrm{119}^{\beta} \:{is}\: \\ $$$$\mathrm{3720}! \\ $$
Commented by Tawa11 last updated on 06/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
