Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 16358 by Tinkutara last updated on 21/Jun/17

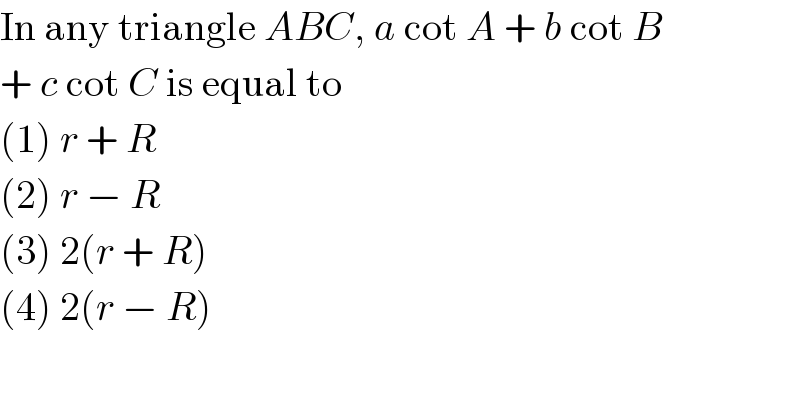
In any triangle ABC, a cot A + b cot B + c cot C is equal to (1) r + R (2) r − R (3) 2(r + R) (4) 2(r − R)

$$\mathrm{In}\:\mathrm{any}\:\mathrm{triangle}\:{ABC},\:{a}\:\mathrm{cot}\:{A}\:+\:{b}\:\mathrm{cot}\:{B} \\ $$$$+\:{c}\:\mathrm{cot}\:{C}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\left(\mathrm{1}\right)\:{r}\:+\:{R} \\ $$$$\left(\mathrm{2}\right)\:{r}\:−\:{R} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{2}\left({r}\:+\:{R}\right) \\ $$$$\left(\mathrm{4}\right)\:\mathrm{2}\left({r}\:−\:{R}\right) \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/Jun/17

answer (3).

$${answer}\:\left(\mathrm{3}\right). \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/Jun/17

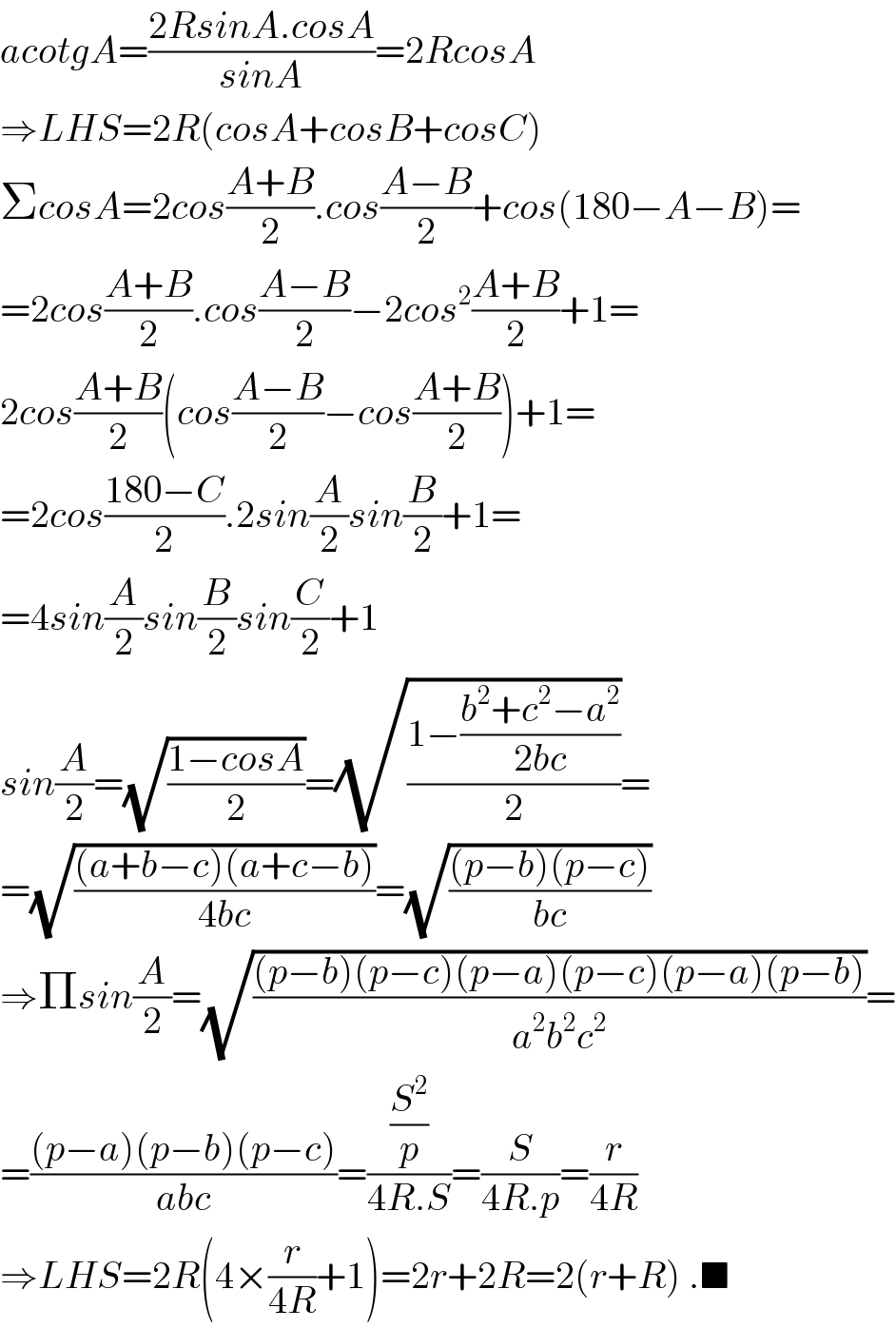
acotgA=((2RsinA.cosA)/(sinA))=2RcosA ⇒LHS=2R(cosA+cosB+cosC) ΣcosA=2cos((A+B)/2).cos((A−B)/2)+cos(180−A−B)= =2cos((A+B)/2).cos((A−B)/2)−2cos^2 ((A+B)/2)+1= 2cos((A+B)/2)(cos((A−B)/2)−cos((A+B)/2))+1= =2cos((180−C)/2).2sin(A/2)sin(B/2)+1= =4sin(A/2)sin(B/2)sin(C/2)+1 sin(A/2)=(√((1−cosA)/2))=(√((1−((b^2 +c^2 −a^2 )/(2bc)))/2))= =(√(((a+b−c)(a+c−b))/(4bc)))=(√(((p−b)(p−c))/(bc))) ⇒Πsin(A/2)=(√(((p−b)(p−c)(p−a)(p−c)(p−a)(p−b))/(a^2 b^2 c^2 )))= =(((p−a)(p−b)(p−c))/(abc))=((S^2 /p)/(4R.S))=(S/(4R.p))=(r/(4R)) ⇒LHS=2R(4×(r/(4R))+1)=2r+2R=2(r+R) .■

$${acotgA}=\frac{\mathrm{2}{RsinA}.{cosA}}{{sinA}}=\mathrm{2}{RcosA} \\ $$$$\Rightarrow{LHS}=\mathrm{2}{R}\left({cosA}+{cosB}+{cosC}\right) \\ $$$$\Sigma{cosA}=\mathrm{2}{cos}\frac{{A}+{B}}{\mathrm{2}}.{cos}\frac{{A}−{B}}{\mathrm{2}}+{cos}\left(\mathrm{180}−{A}−{B}\right)= \\ $$$$=\mathrm{2}{cos}\frac{{A}+{B}}{\mathrm{2}}.{cos}\frac{{A}−{B}}{\mathrm{2}}−\mathrm{2}{cos}^{\mathrm{2}} \frac{{A}+{B}}{\mathrm{2}}+\mathrm{1}= \\ $$$$\mathrm{2}{cos}\frac{{A}+{B}}{\mathrm{2}}\left({cos}\frac{{A}−{B}}{\mathrm{2}}−{cos}\frac{{A}+{B}}{\mathrm{2}}\right)+\mathrm{1}= \\ $$$$=\mathrm{2}{cos}\frac{\mathrm{180}−{C}}{\mathrm{2}}.\mathrm{2}{sin}\frac{{A}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}+\mathrm{1}= \\ $$$$=\mathrm{4}{sin}\frac{{A}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}{sin}\frac{{C}}{\mathrm{2}}+\mathrm{1} \\ $$$${sin}\frac{{A}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}−{cosA}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{1}−\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}}{\mathrm{2}}}= \\ $$$$=\sqrt{\frac{\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)}{\mathrm{4}{bc}}}=\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)}{{bc}}} \\ $$$$\Rightarrow\Pi{sin}\frac{{A}}{\mathrm{2}}=\sqrt{\frac{\left({p}−{b}\right)\left({p}−{c}\right)\left({p}−{a}\right)\left({p}−{c}\right)\left({p}−{a}\right)\left({p}−{b}\right)}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }}= \\ $$$$=\frac{\left({p}−{a}\right)\left({p}−{b}\right)\left({p}−{c}\right)}{{abc}}=\frac{\frac{{S}^{\mathrm{2}} }{{p}}}{\mathrm{4}{R}.{S}}=\frac{{S}}{\mathrm{4}{R}.{p}}=\frac{{r}}{\mathrm{4}{R}} \\ $$$$\Rightarrow{LHS}=\mathrm{2}{R}\left(\mathrm{4}×\frac{{r}}{\mathrm{4}{R}}+\mathrm{1}\right)=\mathrm{2}{r}+\mathrm{2}{R}=\mathrm{2}\left({r}+{R}\right)\:.\blacksquare \\ $$

Commented by Tinkutara last updated on 22/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17

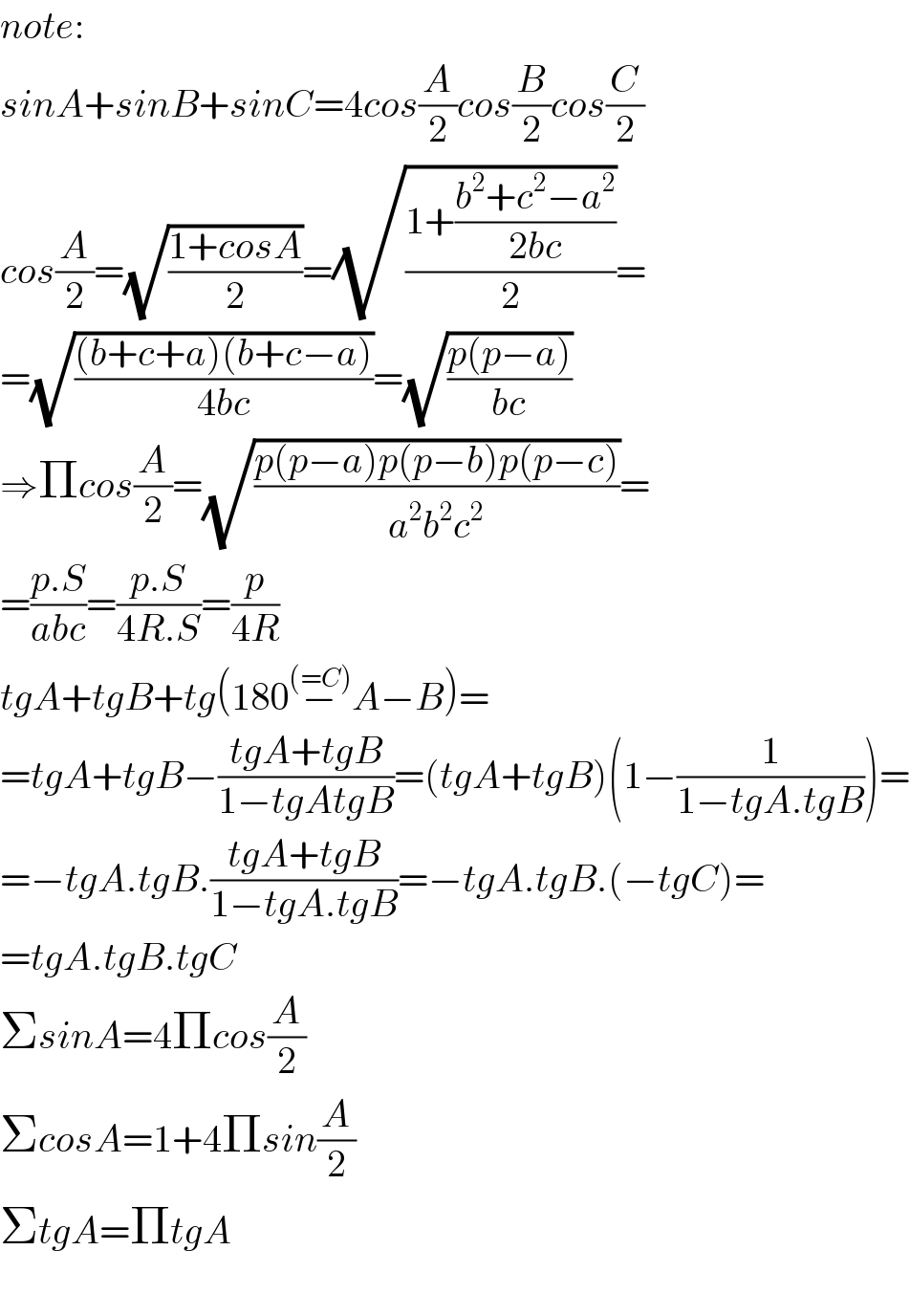
note: sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2) cos(A/2)=(√((1+cosA)/2))=(√((1+((b^2 +c^2 −a^2 )/(2bc)))/2))= =(√(((b+c+a)(b+c−a))/(4bc)))=(√((p(p−a))/(bc))) ⇒Πcos(A/2)=(√((p(p−a)p(p−b)p(p−c))/(a^2 b^2 c^2 )))= =((p.S)/(abc))=((p.S)/(4R.S))=(p/(4R)) tgA+tgB+tg(180−^((=C)) A−B)= =tgA+tgB−((tgA+tgB)/(1−tgAtgB))=(tgA+tgB)(1−(1/(1−tgA.tgB)))= =−tgA.tgB.((tgA+tgB)/(1−tgA.tgB))=−tgA.tgB.(−tgC)= =tgA.tgB.tgC ΣsinA=4Πcos(A/2) ΣcosA=1+4Πsin(A/2) ΣtgA=ΠtgA

$${note}: \\ $$$${sinA}+{sinB}+{sinC}=\mathrm{4}{cos}\frac{{A}}{\mathrm{2}}{cos}\frac{{B}}{\mathrm{2}}{cos}\frac{{C}}{\mathrm{2}} \\ $$$${cos}\frac{{A}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}+{cosA}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{1}+\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}}{\mathrm{2}}}= \\ $$$$=\sqrt{\frac{\left({b}+{c}+{a}\right)\left({b}+{c}−{a}\right)}{\mathrm{4}{bc}}}=\sqrt{\frac{{p}\left({p}−{a}\right)}{{bc}}} \\ $$$$\Rightarrow\Pi{cos}\frac{{A}}{\mathrm{2}}=\sqrt{\frac{{p}\left({p}−{a}\right){p}\left({p}−{b}\right){p}\left({p}−{c}\right)}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }}= \\ $$$$=\frac{{p}.{S}}{{abc}}=\frac{{p}.{S}}{\mathrm{4}{R}.{S}}=\frac{{p}}{\mathrm{4}{R}} \\ $$$${tgA}+{tgB}+{tg}\left(\mathrm{180}\overset{\left(={C}\right)} {−}{A}−{B}\right)= \\ $$$$={tgA}+{tgB}−\frac{{tgA}+{tgB}}{\mathrm{1}−{tgAtgB}}=\left({tgA}+{tgB}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{tgA}.{tgB}}\right)= \\ $$$$=−{tgA}.{tgB}.\frac{{tgA}+{tgB}}{\mathrm{1}−{tgA}.{tgB}}=−{tgA}.{tgB}.\left(−{tgC}\right)= \\ $$$$={tgA}.{tgB}.{tgC} \\ $$$$\Sigma{sinA}=\mathrm{4}\Pi{cos}\frac{{A}}{\mathrm{2}} \\ $$$$\Sigma{cosA}=\mathrm{1}+\mathrm{4}\Pi{sin}\frac{{A}}{\mathrm{2}} \\ $$$$\Sigma{tgA}=\Pi{tgA} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com