
Question Number 163700 by blackmamba last updated on 09/Jan/22
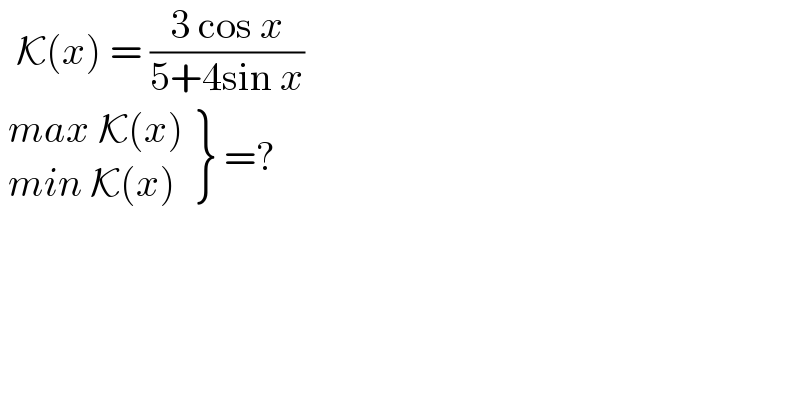
$$\:\:\mathcal{K}\left({x}\right)\:=\:\frac{\mathrm{3}\:\mathrm{cos}\:{x}}{\mathrm{5}+\mathrm{4sin}\:{x}} \\ $$$$\:\left.\begin{matrix}{{max}\:\mathcal{K}\left({x}\right)}\\{{min}\:\mathcal{K}\left({x}\right)}\end{matrix}\right\}\:=? \\ $$
Answered by mr W last updated on 10/Jan/22

$$\frac{\mathrm{3}\:\mathrm{cos}\:{x}}{\mathrm{5}+\mathrm{4}\:\mathrm{sin}\:{x}}={k} \\ $$$$\mathrm{3}\:\mathrm{cos}\:{x}−\mathrm{4}{k}\:\mathrm{sin}\:{x}=\mathrm{5}{k} \\ $$$$\frac{\mathrm{3}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{4}{k}\right)^{\mathrm{2}} }}\:\mathrm{cos}\:{x}−\frac{\mathrm{4}{k}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{4}{k}\right)^{\mathrm{2}} }}\:\mathrm{sin}\:{x}=\frac{\mathrm{5}{k}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{4}{k}\right)^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\alpha\:\mathrm{cos}\:{x}−\mathrm{sin}\:\alpha\:\mathrm{sin}\:{x}=\frac{\mathrm{5}{k}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{4}{k}\right)^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\left({x}+\alpha\right)=\frac{\mathrm{5}{k}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{4}{k}\right)^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{5}{k}}{\:\sqrt{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{4}{k}\right)^{\mathrm{2}} }}\leqslant\mathrm{1} \\ $$$$\mathrm{25}{k}^{\mathrm{2}} \leqslant\mathrm{9}+\mathrm{16}{k}^{\mathrm{2}} \\ $$$${k}^{\mathrm{2}} \leqslant\mathrm{1} \\ $$$$−\mathrm{1}\leqslant{k}\leqslant\mathrm{1} \\ $$$${k}\left({x}\right)_{{min}} =−\mathrm{1} \\ $$$${k}\left({x}\right)_{{max}} =\mathrm{1} \\ $$
Answered by MJS_new last updated on 09/Jan/22
![((3c)/(5+4s))=±((3(√(1−s^2 )))/(5+4s)) ±(d/ds)[((3(√(1−s^2 )))/(5+4s))]=0 ∓((3(5s+4))/((4s+5)^2 (√(1−s^2 ))))=0 ⇒ s=−(4/5) ⇒ −1≤K≤1](Q163701.png)
$$\frac{\mathrm{3}{c}}{\mathrm{5}+\mathrm{4}{s}}=\pm\frac{\mathrm{3}\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }}{\mathrm{5}+\mathrm{4}{s}} \\ $$$$\pm\frac{{d}}{{ds}}\left[\frac{\mathrm{3}\sqrt{\mathrm{1}−{s}^{\mathrm{2}} }}{\mathrm{5}+\mathrm{4}{s}}\right]=\mathrm{0} \\ $$$$\mp\frac{\mathrm{3}\left(\mathrm{5}{s}+\mathrm{4}\right)}{\left(\mathrm{4}{s}+\mathrm{5}\right)^{\mathrm{2}} \sqrt{\mathrm{1}−{s}^{\mathrm{2}} }}=\mathrm{0}\:\Rightarrow\:{s}=−\frac{\mathrm{4}}{\mathrm{5}}\:\Rightarrow\:−\mathrm{1}\leqslant{K}\leqslant\mathrm{1} \\ $$
Commented by blackmamba last updated on 09/Jan/22

$${yes} \\ $$
Answered by cortano1 last updated on 09/Jan/22
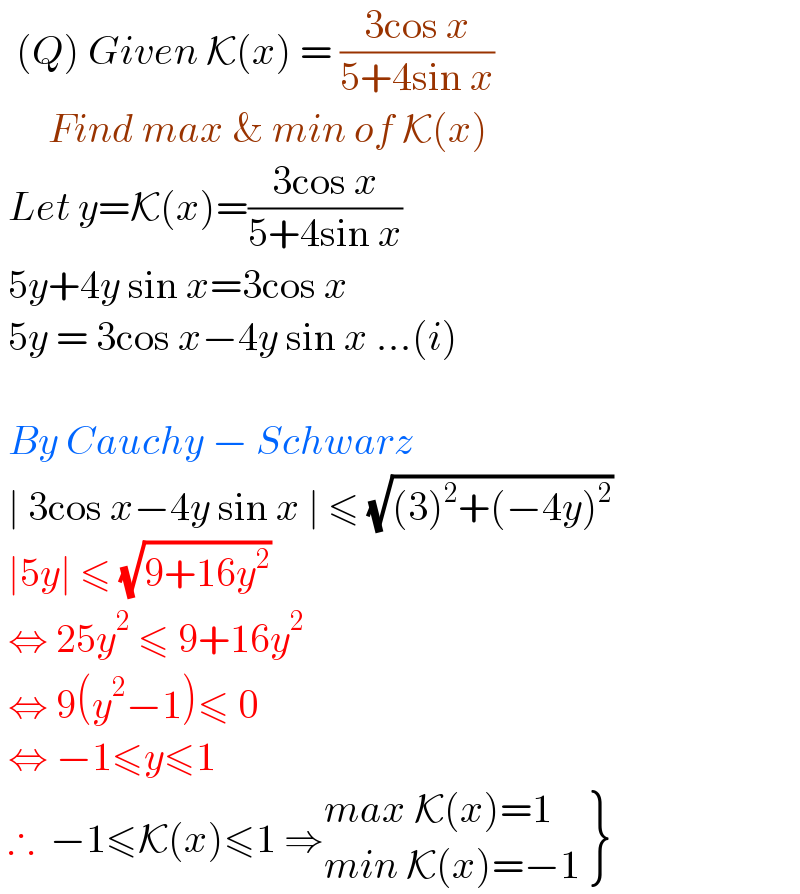
$$\:\:\left({Q}\right)\:{Given}\:\mathcal{K}\left({x}\right)\:=\:\frac{\mathrm{3cos}\:{x}}{\mathrm{5}+\mathrm{4sin}\:{x}}\: \\ $$$$\:\:\:\:\:\:{Find}\:{max}\:\&\:{min}\:{of}\:\mathcal{K}\left({x}\right) \\ $$$$\:{Let}\:{y}=\mathcal{K}\left({x}\right)=\frac{\mathrm{3cos}\:{x}}{\mathrm{5}+\mathrm{4sin}\:{x}} \\ $$$$\:\mathrm{5}{y}+\mathrm{4}{y}\:\mathrm{sin}\:{x}=\mathrm{3cos}\:{x}\: \\ $$$$\:\mathrm{5}{y}\:=\:\mathrm{3cos}\:{x}−\mathrm{4}{y}\:\mathrm{sin}\:{x}\:...\left({i}\right) \\ $$$$ \\ $$$$\:{By}\:{Cauchy}\:−\:{Schwarz}\: \\ $$$$\:\mid\:\mathrm{3cos}\:{x}−\mathrm{4}{y}\:\mathrm{sin}\:{x}\:\mid\:\leqslant\:\sqrt{\left(\mathrm{3}\right)^{\mathrm{2}} +\left(−\mathrm{4}{y}\right)^{\mathrm{2}} } \\ $$$$\:\mid\mathrm{5}{y}\mid\:\leqslant\:\sqrt{\mathrm{9}+\mathrm{16}{y}^{\mathrm{2}} } \\ $$$$\:\Leftrightarrow\:\mathrm{25}{y}^{\mathrm{2}} \:\leqslant\:\mathrm{9}+\mathrm{16}{y}^{\mathrm{2}} \\ $$$$\:\Leftrightarrow\:\mathrm{9}\left({y}^{\mathrm{2}} −\mathrm{1}\right)\leqslant\:\mathrm{0} \\ $$$$\:\Leftrightarrow\:−\mathrm{1}\leqslant{y}\leqslant\mathrm{1}\: \\ $$$$\:\therefore\:\:−\mathrm{1}\leqslant\mathcal{K}\left({x}\right)\leqslant\mathrm{1}\:\Rightarrow\left.\begin{matrix}{{max}\:\mathcal{K}\left({x}\right)=\mathrm{1}}\\{{min}\:\mathcal{K}\left({x}\right)=−\mathrm{1}}\end{matrix}\right\} \\ $$
Commented by blackmamba last updated on 09/Jan/22

$${yes} \\ $$
