
Question Number 165099 by SANOGO last updated on 26/Jan/22
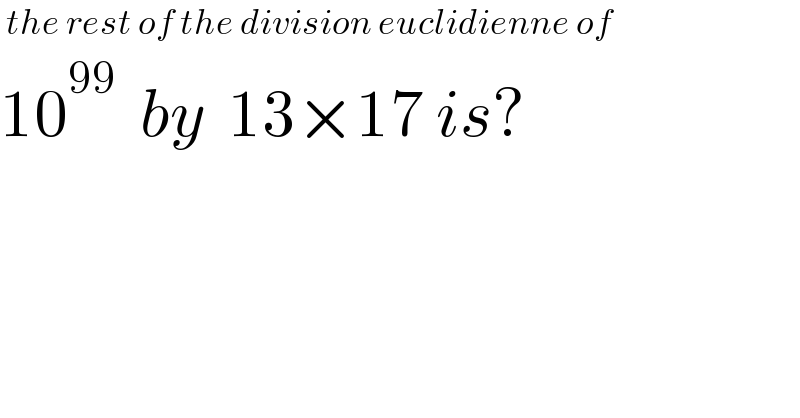
$$\:{the}\:{rest}\:{of}\:{the}\:{division}\:{euclidienne}\:{of} \\ $$$$\mathrm{10}^{\mathrm{99}} \:\:{by}\:\:\mathrm{13}×\mathrm{17}\:{is}? \\ $$
Commented by Rasheed.Sindhi last updated on 26/Jan/22
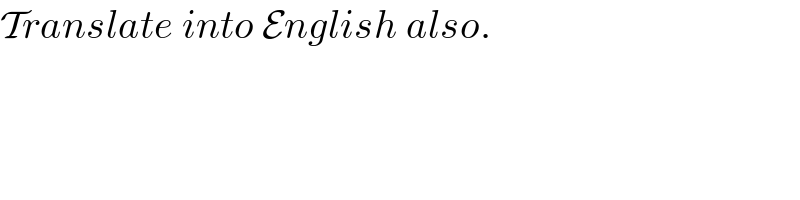
$$\mathcal{T}{ranslate}\:{into}\:\mathcal{E}{nglish}\:{also}. \\ $$
Answered by mr W last updated on 27/Jan/22

$$\mathrm{13}×\mathrm{17}=\mathrm{221} \\ $$$$\mathrm{10}^{\mathrm{99}} =\left(\mathrm{1000}\right)^{\mathrm{33}} \\ $$$$=\left(\mathrm{4}×\mathrm{221}+\mathrm{116}\right)^{\mathrm{33}} \\ $$$$\vDash\mathrm{116}^{\mathrm{33}} \\ $$$$=\mathrm{116}×\left(\mathrm{60}×\mathrm{221}+\mathrm{196}\right)^{\mathrm{16}} \\ $$$$\vDash\mathrm{116}×\mathrm{196}^{\mathrm{16}} \\ $$$$=\mathrm{116}×\left(\mathrm{173}×\mathrm{221}+\mathrm{183}\right)^{\mathrm{8}} \\ $$$$\vDash\mathrm{116}×\mathrm{183}^{\mathrm{8}} \\ $$$$=\mathrm{116}×\left(\mathrm{151}×\mathrm{221}+\mathrm{118}\right)^{\mathrm{4}} \\ $$$$\vDash\mathrm{116}×\mathrm{118}^{\mathrm{4}} \\ $$$$=\mathrm{116}×\left(\mathrm{60}×\mathrm{221}+\mathrm{664}\right)^{\mathrm{2}} \\ $$$$\vDash\mathrm{116}×\mathrm{664}^{\mathrm{2}} \\ $$$$=\mathrm{116}×\left(\mathrm{1995}×\mathrm{221}+\mathrm{1}\right) \\ $$$$\vDash\mathrm{116}\:={answer} \\ $$$${with}\:\vDash\:{i}\:{mean}\: \\ $$$$``{has}\:{the}\:{same}\:{remainder}\:{as}'' \\ $$
Answered by Rasheed.Sindhi last updated on 27/Jan/22
![Another way... Say, 10^(99) ≡x(mod 221) [∵ 13×17=221] ∵ gcd(10,221)=1 ∴ 10^(φ(221)) ≡1(mod 221) Now, φ(221)=221(1−(1/(13)))(1−(1/(17)))=192 ∴ 10^(192) ≡1(mod 221) Trying for dicferent divisors of 192 We can see that 10^(48) ≡1(mod 221) (10^(48) )^2 ≡(1)^2 (mod 221) 10^(96) ≡1(mod 221).........(i) Also can be observed that 10^3 ≡116(mod 221)......(ii) (i)×(ii): 10^(99) ≡116(mod 221) x=116](Q165225.png)
$$\mathrm{Another}\:\mathrm{way}... \\ $$$${Say},\:\mathrm{10}^{\mathrm{99}} \equiv{x}\left({mod}\:\mathrm{221}\right)\:\:\:\left[\because\:\mathrm{13}×\mathrm{17}=\mathrm{221}\right] \\ $$$$\:\because\:\mathrm{gcd}\left(\mathrm{10},\mathrm{221}\right)=\mathrm{1} \\ $$$$\therefore\:\mathrm{10}^{\phi\left(\mathrm{221}\right)} \equiv\mathrm{1}\left({mod}\:\mathrm{221}\right) \\ $$$${Now},\:\phi\left(\mathrm{221}\right)=\mathrm{221}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{13}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{17}}\right)=\mathrm{192} \\ $$$$\therefore\:\mathrm{10}^{\mathrm{192}} \equiv\mathrm{1}\left({mod}\:\mathrm{221}\right) \\ $$$$\mathcal{T}{rying}\:{for}\:{dicferent}\:{divisors}\:{of}\:\mathrm{192} \\ $$$${We}\:{can}\:{see}\:{that} \\ $$$$\:\:\:\mathrm{10}^{\mathrm{48}} \equiv\mathrm{1}\left({mod}\:\mathrm{221}\right) \\ $$$$\:\:\:\left(\mathrm{10}^{\mathrm{48}} \right)^{\mathrm{2}} \equiv\left(\mathrm{1}\right)^{\mathrm{2}} \left({mod}\:\mathrm{221}\right) \\ $$$$\:\:\:\:\:\mathrm{10}^{\mathrm{96}} \equiv\mathrm{1}\left({mod}\:\mathrm{221}\right).........\left({i}\right) \\ $$$${Also}\:{can}\:{be}\:{observed}\:{that} \\ $$$$\:\:\:\:\:\:\mathrm{10}^{\mathrm{3}} \equiv\mathrm{116}\left({mod}\:\mathrm{221}\right)......\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right):\:\:\mathrm{10}^{\mathrm{99}} \equiv\mathrm{116}\left({mod}\:\mathrm{221}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{116} \\ $$
