Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 166208 by ajfour last updated on 15/Feb/22

Commented by ajfour last updated on 15/Feb/22

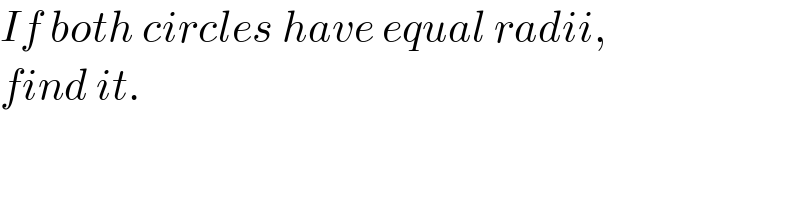
If both circles have equal radii, find it.

$${If}\:{both}\:{circles}\:{have}\:{equal}\:{radii}, \\ $$$${find}\:{it}. \\ $$

Answered by Eulerian last updated on 15/Feb/22

AB^(−) = (√(r^2 +4r^2 )) = (√5)r ∠ BAC = tan^(−1) ((r/(2r))) + cos^(−1) ((r/(2r))) = tan^(−1) ((1/2)) + cos^(−1) ((1/2)) ∴ By pythagorean identity, we have ((BC^(−) )/( (√5)r)) = sin(tan^(−1) ((1/2)) + cos^(−1) ((1/2))) = sin(tan^(−1) ((1/2)))∙cos(cos^(−1) ((1/2))) + cos(tan^(−1) ((1/2)))∙sin(cos^(−1) ((1/2))) = (((√5)/5))((1/2)) + (((2(√5))/5))(((√3)/2)) = (((√5)+2(√(15)))/(10)) ∴ BC^(−) = (((1+2(√3))/2))∙r Thus, we now have: (((1+2(√3))/2))∙r + r = r^2 r = ((1+2(√3))/2) + 1 = ((3+2(√3))/2) units

$$\:\overline {\mathrm{AB}}\:=\:\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{4r}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{5}}\mathrm{r} \\ $$$$\:\angle\:\mathrm{BAC}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{r}}{\mathrm{2r}}\right)\:+\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{r}}{\mathrm{2r}}\right)\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:+\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\therefore\:\mathrm{By}\:\mathrm{pythagorean}\:\mathrm{identity},\:\mathrm{we}\:\mathrm{have} \\ $$$$\:\frac{\overline {\mathrm{BC}}}{\:\sqrt{\mathrm{5}}\mathrm{r}}\:=\:\mathrm{sin}\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:+\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\mathrm{sin}\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\centerdot\mathrm{cos}\left(\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\:+\:\mathrm{cos}\left(\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\centerdot\mathrm{sin}\left(\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:+\:\left(\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}}\right)\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{15}}}{\mathrm{10}} \\ $$$$\:\therefore \\ $$$$\:\overline {\mathrm{BC}}\:=\:\left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\centerdot\mathrm{r} \\ $$$$\: \\ $$$$\:\mathrm{Thus},\:\mathrm{we}\:\mathrm{now}\:\mathrm{have}: \\ $$$$\:\left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\centerdot\mathrm{r}\:+\:\mathrm{r}\:=\:\mathrm{r}^{\mathrm{2}} \\ $$$$\:\mathrm{r}\:=\:\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\:+\:\mathrm{1}\:=\:\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\mathrm{units} \\ $$

Commented by ajfour last updated on 15/Feb/22

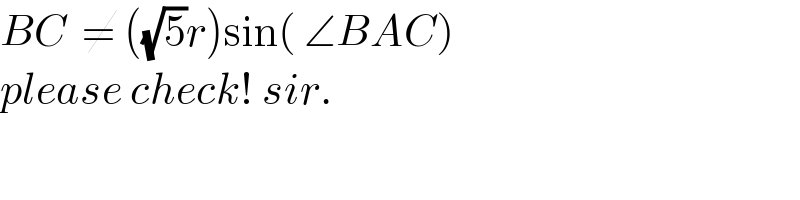
BC ≠ ((√5)r)sin( ∠BAC) please check! sir.

$${BC}\:\:\neq\:\left(\sqrt{\mathrm{5}}{r}\right)\mathrm{sin}\left(\:\angle{BAC}\right) \\ $$$${please}\:{check}!\:{sir}. \\ $$

Answered by mr W last updated on 15/Feb/22

Commented by Tawa11 last updated on 16/Feb/22

Great sir.

$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 16/Feb/22

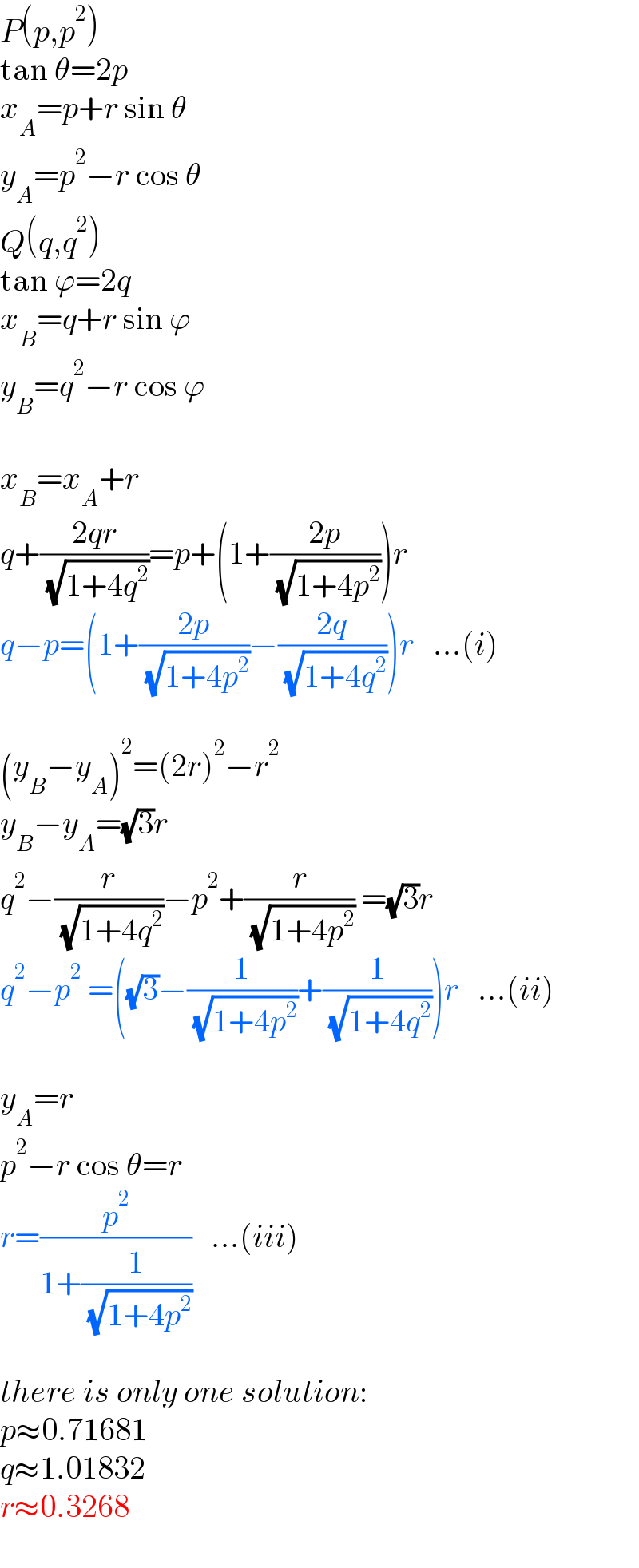
P(p,p^2 ) tan θ=2p x_A =p+r sin θ y_A =p^2 −r cos θ Q(q,q^2 ) tan ϕ=2q x_B =q+r sin ϕ y_B =q^2 −r cos ϕ x_B =x_A +r q+((2qr)/( (√(1+4q^2 ))))=p+(1+((2p)/( (√(1+4p^2 )))))r q−p=(1+((2p)/( (√(1+4p^2 ))))−((2q)/( (√(1+4q^2 )))))r ...(i) (y_B −y_A )^2 =(2r)^2 −r^2 y_B −y_A =(√3)r q^2 −(r/( (√(1+4q^2 ))))−p^2 +(r/( (√(1+4p^2 )))) =(√3)r q^2 −p^2 =((√3)−(1/( (√(1+4p^2 ))))+(1/( (√(1+4q^2 )))))r ...(ii) y_A =r p^2 −r cos θ=r r=(p^2 /(1+(1/( (√(1+4p^2 )))))) ...(iii) there is only one solution: p≈0.71681 q≈1.01832 r≈0.3268

$${P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}{p} \\ $$$${x}_{{A}} ={p}+{r}\:\mathrm{sin}\:\theta \\ $$$${y}_{{A}} ={p}^{\mathrm{2}} −{r}\:\mathrm{cos}\:\theta \\ $$$${Q}\left({q},{q}^{\mathrm{2}} \right) \\ $$$$\mathrm{tan}\:\varphi=\mathrm{2}{q} \\ $$$${x}_{{B}} ={q}+{r}\:\mathrm{sin}\:\varphi \\ $$$${y}_{{B}} ={q}^{\mathrm{2}} −{r}\:\mathrm{cos}\:\varphi \\ $$$$ \\ $$$${x}_{{B}} ={x}_{{A}} +{r} \\ $$$${q}+\frac{\mathrm{2}{qr}}{\:\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}={p}+\left(\mathrm{1}+\frac{\mathrm{2}{p}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}\right){r} \\ $$$${q}−{p}=\left(\mathrm{1}+\frac{\mathrm{2}{p}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}−\frac{\mathrm{2}{q}}{\:\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}\right){r}\:\:\:...\left({i}\right) \\ $$$$ \\ $$$$\left({y}_{{B}} −{y}_{{A}} \right)^{\mathrm{2}} =\left(\mathrm{2}{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$${y}_{{B}} −{y}_{{A}} =\sqrt{\mathrm{3}}{r} \\ $$$${q}^{\mathrm{2}} −\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}−{p}^{\mathrm{2}} +\frac{{r}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}\:=\sqrt{\mathrm{3}}{r} \\ $$$${q}^{\mathrm{2}} −{p}^{\mathrm{2}} \:=\left(\sqrt{\mathrm{3}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{q}^{\mathrm{2}} }}\right){r}\:\:\:...\left({ii}\right) \\ $$$$ \\ $$$${y}_{{A}} ={r} \\ $$$${p}^{\mathrm{2}} −{r}\:\mathrm{cos}\:\theta={r} \\ $$$${r}=\frac{{p}^{\mathrm{2}} }{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{4}{p}^{\mathrm{2}} }}}\:\:\:...\left({iii}\right) \\ $$$$ \\ $$$${there}\:{is}\:{only}\:{one}\:{solution}: \\ $$$${p}\approx\mathrm{0}.\mathrm{71681} \\ $$$${q}\approx\mathrm{1}.\mathrm{01832} \\ $$$${r}\approx\mathrm{0}.\mathrm{3268} \\ $$

Commented by mr W last updated on 16/Feb/22

Commented by mr W last updated on 16/Feb/22

Terms of Service

Privacy Policy

Contact: info@tinkutara.com