Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

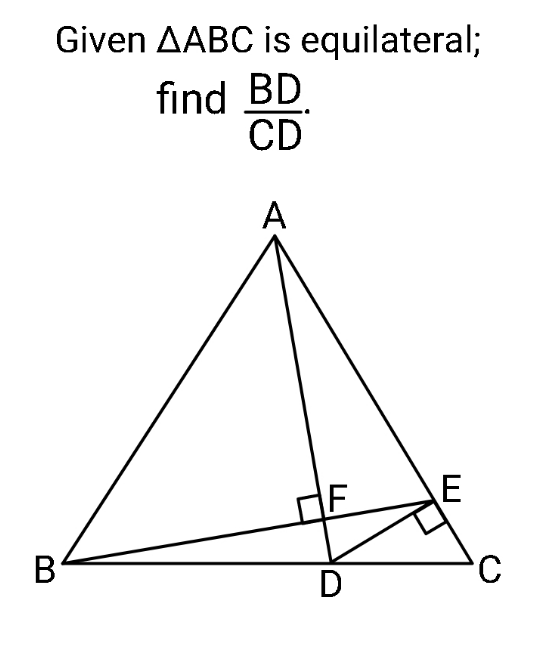
Question Number 166701 by ajfour last updated on 25/Feb/22

Answered by mr W last updated on 26/Feb/22

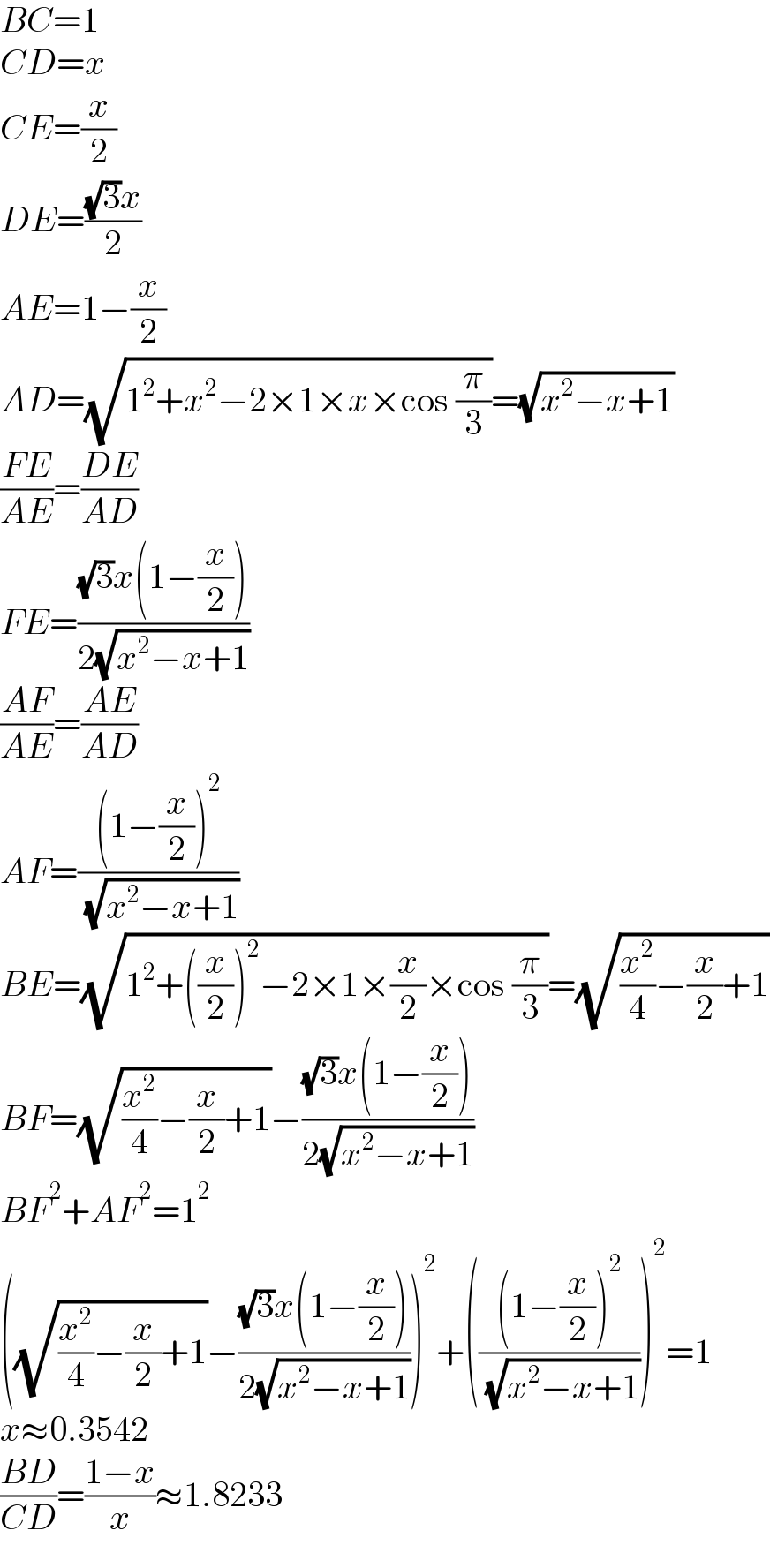
BC=1 CD=x CE=(x/2) DE=(((√3)x)/2) AE=1−(x/2) AD=(√(1^2 +x^2 −2×1×x×cos (π/3)))=(√(x^2 −x+1)) ((FE)/(AE))=((DE)/(AD)) FE=(((√3)x(1−(x/2)))/(2(√(x^2 −x+1)))) ((AF)/(AE))=((AE)/(AD)) AF=(((1−(x/2))^2 )/( (√(x^2 −x+1)))) BE=(√(1^2 +((x/2))^2 −2×1×(x/2)×cos (π/3)))=(√((x^2 /4)−(x/2)+1)) BF=(√((x^2 /4)−(x/2)+1))−(((√3)x(1−(x/2)))/(2(√(x^2 −x+1)))) BF^2 +AF^2 =1^2 ((√((x^2 /4)−(x/2)+1))−(((√3)x(1−(x/2)))/(2(√(x^2 −x+1)))))^2 +((((1−(x/2))^2 )/( (√(x^2 −x+1)))))^2 =1 x≈0.3542 ((BD)/(CD))=((1−x)/x)≈1.8233

$${BC}=\mathrm{1} \\ $$$${CD}={x} \\ $$$${CE}=\frac{{x}}{\mathrm{2}} \\ $$$${DE}=\frac{\sqrt{\mathrm{3}}{x}}{\mathrm{2}} \\ $$$${AE}=\mathrm{1}−\frac{{x}}{\mathrm{2}} \\ $$$${AD}=\sqrt{\mathrm{1}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×{x}×\mathrm{cos}\:\frac{\pi}{\mathrm{3}}}=\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$\frac{{FE}}{{AE}}=\frac{{DE}}{{AD}} \\ $$$${FE}=\frac{\sqrt{\mathrm{3}}{x}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$$$\frac{{AF}}{{AE}}=\frac{{AE}}{{AD}} \\ $$$${AF}=\frac{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$$${BE}=\sqrt{\mathrm{1}^{\mathrm{2}} +\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{1}×\frac{{x}}{\mathrm{2}}×\mathrm{cos}\:\frac{\pi}{\mathrm{3}}}=\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}}{\mathrm{2}}+\mathrm{1}} \\ $$$${BF}=\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}}{\mathrm{2}}+\mathrm{1}}−\frac{\sqrt{\mathrm{3}}{x}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$$${BF}^{\mathrm{2}} +{AF}^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \\ $$$$\left(\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{{x}}{\mathrm{2}}+\mathrm{1}}−\frac{\sqrt{\mathrm{3}}{x}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\right)^{\mathrm{2}} +\left(\frac{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${x}\approx\mathrm{0}.\mathrm{3542} \\ $$$$\frac{{BD}}{{CD}}=\frac{\mathrm{1}−{x}}{{x}}\approx\mathrm{1}.\mathrm{8233} \\ $$

Commented by Tawa11 last updated on 26/Feb/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by ajfour last updated on 26/Feb/22

Thanks sir. I got it exact easily somehow!

Commented by mr W last updated on 26/Feb/22

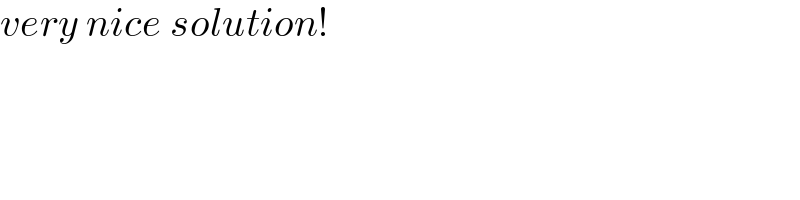
very nice solution!

$${very}\:{nice}\:{solution}! \\ $$

Answered by ajfour last updated on 26/Feb/22

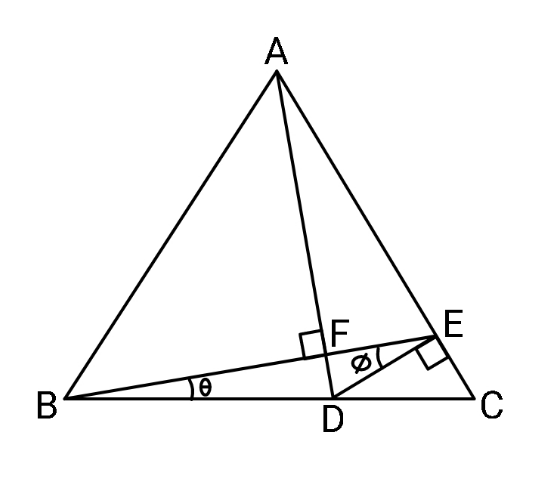
Commented by ajfour last updated on 26/Feb/22

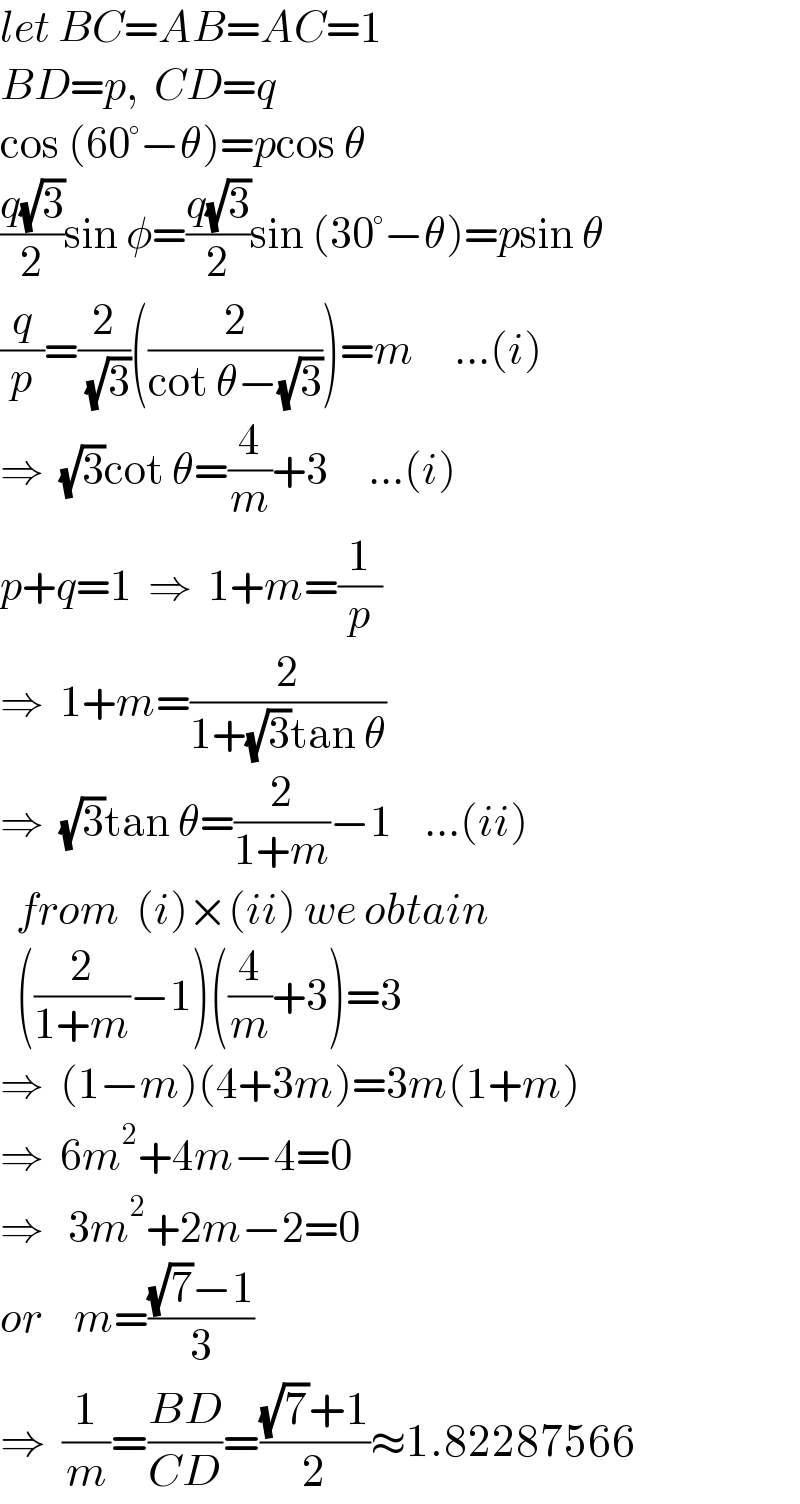
let BC=AB=AC=1 BD=p, CD=q cos (60°−θ)=pcos θ ((q(√3))/2)sin φ=((q(√3))/2)sin (30°−θ)=psin θ (q/p)=(2/( (√3)))((2/(cot θ−(√3))))=m ...(i) ⇒ (√3)cot θ=(4/m)+3 ...(i) p+q=1 ⇒ 1+m=(1/p) ⇒ 1+m=(2/(1+(√3)tan θ)) ⇒ (√3)tan θ=(2/(1+m))−1 ...(ii) from (i)×(ii) we obtain ((2/(1+m))−1)((4/m)+3)=3 ⇒ (1−m)(4+3m)=3m(1+m) ⇒ 6m^2 +4m−4=0 ⇒ 3m^2 +2m−2=0 or m=(((√7)−1)/3) ⇒ (1/m)=((BD)/(CD))=(((√7)+1)/2)≈1.82287566

$${let}\:{BC}={AB}={AC}=\mathrm{1} \\ $$$${BD}={p},\:\:{CD}={q} \\ $$$$\mathrm{cos}\:\left(\mathrm{60}°−\theta\right)={p}\mathrm{cos}\:\theta \\ $$$$\frac{{q}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\phi=\frac{{q}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\left(\mathrm{30}°−\theta\right)={p}\mathrm{sin}\:\theta \\ $$$$\frac{{q}}{{p}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\frac{\mathrm{2}}{\mathrm{cot}\:\theta−\sqrt{\mathrm{3}}}\right)={m}\:\:\:\:\:...\left({i}\right) \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{3}}\mathrm{cot}\:\theta=\frac{\mathrm{4}}{{m}}+\mathrm{3}\:\:\:\:\:...\left({i}\right) \\ $$$${p}+{q}=\mathrm{1}\:\:\Rightarrow\:\:\mathrm{1}+{m}=\frac{\mathrm{1}}{{p}} \\ $$$$\Rightarrow\:\:\mathrm{1}+{m}=\frac{\mathrm{2}}{\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{tan}\:\theta} \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{3}}\mathrm{tan}\:\theta=\frac{\mathrm{2}}{\mathrm{1}+{m}}−\mathrm{1}\:\:\:\:...\left({ii}\right) \\ $$$$\:\:{from}\:\:\left({i}\right)×\left({ii}\right)\:{we}\:{obtain} \\ $$$$\:\:\left(\frac{\mathrm{2}}{\mathrm{1}+{m}}−\mathrm{1}\right)\left(\frac{\mathrm{4}}{{m}}+\mathrm{3}\right)=\mathrm{3} \\ $$$$\Rightarrow\:\:\left(\mathrm{1}−{m}\right)\left(\mathrm{4}+\mathrm{3}{m}\right)=\mathrm{3}{m}\left(\mathrm{1}+{m}\right) \\ $$$$\Rightarrow\:\:\mathrm{6}{m}^{\mathrm{2}} +\mathrm{4}{m}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{3}{m}^{\mathrm{2}} +\mathrm{2}{m}−\mathrm{2}=\mathrm{0} \\ $$$${or}\:\:\:\:{m}=\frac{\sqrt{\mathrm{7}}−\mathrm{1}}{\mathrm{3}}\:\: \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{{m}}=\frac{{BD}}{{CD}}=\frac{\sqrt{\mathrm{7}}+\mathrm{1}}{\mathrm{2}}\approx\mathrm{1}.\mathrm{82287566} \\ $$

Commented by Tawa11 last updated on 03/Mar/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com