Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 167105 by mnjuly1970 last updated on 06/Mar/22

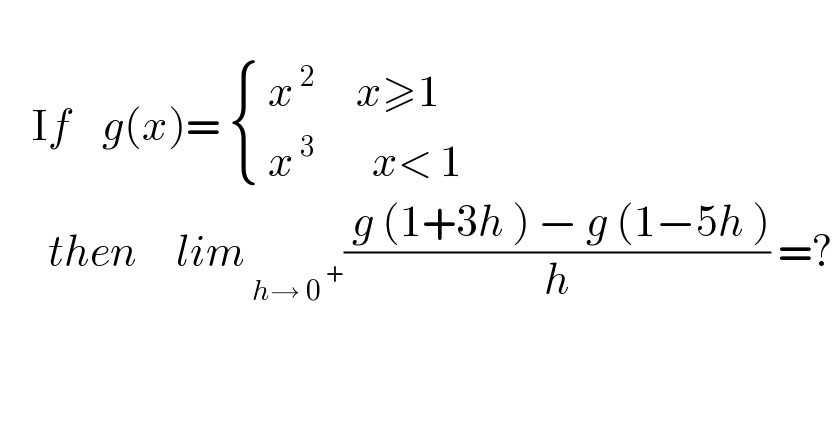
If g(x)= { (( x^( 2) x≥1)),(( x^( 3) x< 1)) :} then lim_( h→ 0^( +) ) (( g (1+3h ) − g (1−5h ))/h) =?

$$ \\ $$ $$\:\:\:\:\mathrm{I}{f}\:\:\:\:{g}\left({x}\right)=\:\begin{cases}{\:{x}^{\:\mathrm{2}} \:\:\:\:\:{x}\geqslant\mathrm{1}}\\{\:{x}^{\:\mathrm{3}} \:\:\:\:\:\:\:{x}<\:\mathrm{1}}\end{cases}\: \\ $$ $$\:\:\:\:\:\:{then}\:\:\:\:\:{lim}_{\:{h}\rightarrow\:\mathrm{0}^{\:+} } \frac{\:{g}\:\left(\mathrm{1}+\mathrm{3}{h}\:\right)\:−\:{g}\:\left(\mathrm{1}−\mathrm{5}{h}\:\right)}{{h}}\:=? \\ $$

Answered by greogoury55 last updated on 06/Mar/22

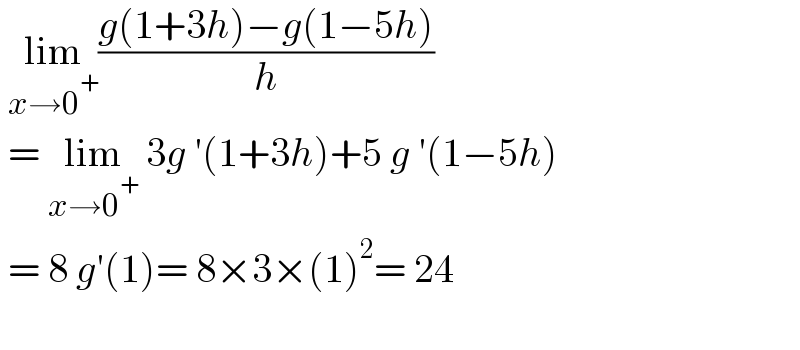
lim_(x→0^+ ) ((g(1+3h)−g(1−5h))/h) = lim_(x→0^+ ) 3g ′(1+3h)+5 g ′(1−5h) = 8 g′(1)= 8×3×(1)^2 = 24

$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{g}\left(\mathrm{1}+\mathrm{3}{h}\right)−{g}\left(\mathrm{1}−\mathrm{5}{h}\right)}{{h}} \\ $$ $$\:=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\mathrm{3}{g}\:'\left(\mathrm{1}+\mathrm{3}{h}\right)+\mathrm{5}\:{g}\:'\left(\mathrm{1}−\mathrm{5}{h}\right) \\ $$ $$\:=\:\mathrm{8}\:{g}'\left(\mathrm{1}\right)=\:\mathrm{8}×\mathrm{3}×\left(\mathrm{1}\right)^{\mathrm{2}} =\:\mathrm{24} \\ $$ $$ \\ $$

Commented bymnjuly1970 last updated on 06/Mar/22

please recheck

$$\:{please}\:{recheck} \\ $$

Answered by Mathspace last updated on 07/Mar/22

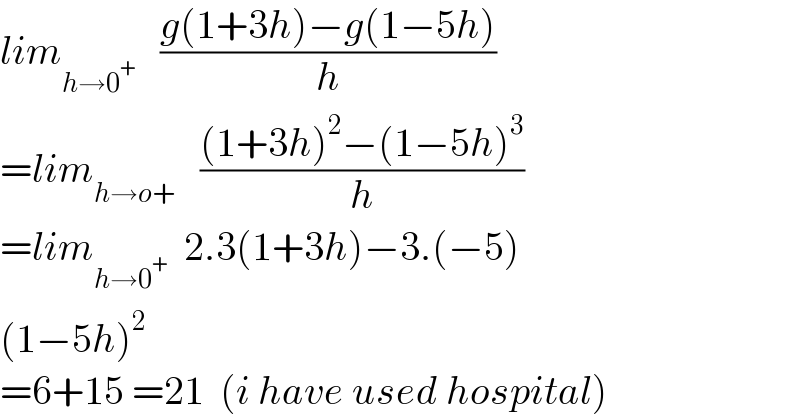
lim_(h→0^+ ) ((g(1+3h)−g(1−5h))/h) =lim_(h→o+) (((1+3h)^2 −(1−5h)^3 )/h) =lim_(h→0^+ ) 2.3(1+3h)−3.(−5) (1−5h)^2 =6+15 =21 (i have used hospital)

$${lim}_{{h}\rightarrow\mathrm{0}^{+} } \:\:\:\frac{{g}\left(\mathrm{1}+\mathrm{3}{h}\right)−{g}\left(\mathrm{1}−\mathrm{5}{h}\right)}{{h}} \\ $$ $$={lim}_{{h}\rightarrow{o}+} \:\:\:\frac{\left(\mathrm{1}+\mathrm{3}{h}\right)^{\mathrm{2}} −\left(\mathrm{1}−\mathrm{5}{h}\right)^{\mathrm{3}} }{{h}} \\ $$ $$={lim}_{{h}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{2}.\mathrm{3}\left(\mathrm{1}+\mathrm{3}{h}\right)−\mathrm{3}.\left(−\mathrm{5}\right) \\ $$ $$\left(\mathrm{1}−\mathrm{5}{h}\right)^{\mathrm{2}} \\ $$ $$=\mathrm{6}+\mathrm{15}\:=\mathrm{21}\:\:\left({i}\:{have}\:{used}\:{hospital}\right) \\ $$

Answered by alephzero last updated on 08/Mar/22

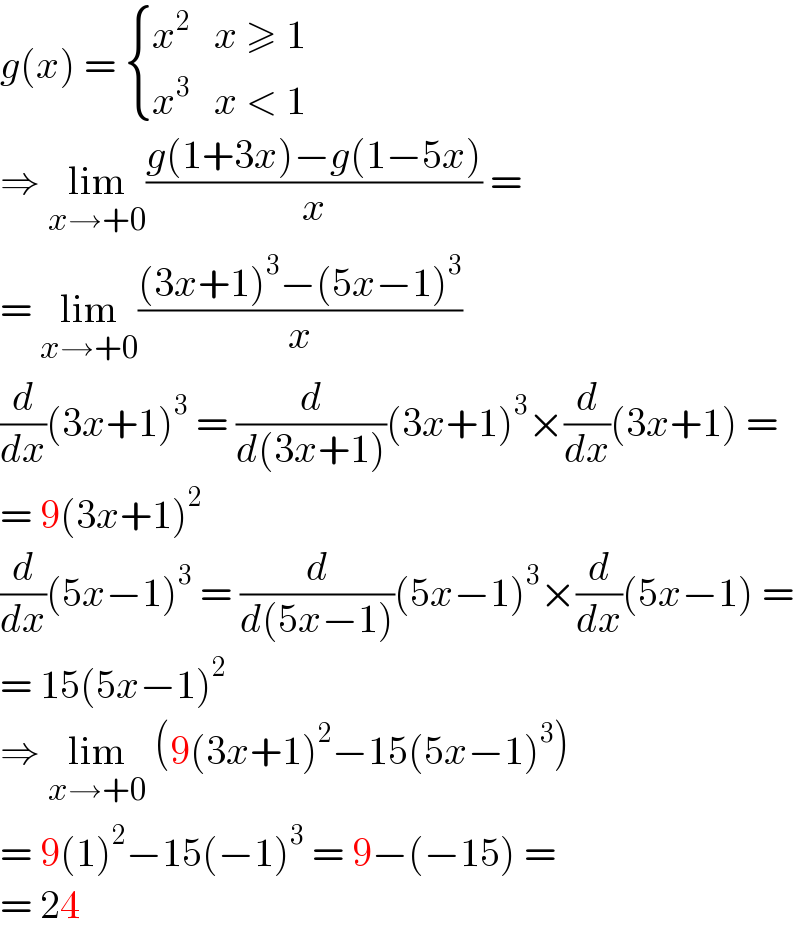
g(x) = { (x^2 ,(x ≥ 1)),(x^3 ,(x < 1)) :} ⇒ lim_(x→+0) ((g(1+3x)−g(1−5x))/x) = = lim_(x→+0) (((3x+1)^3 −(5x−1)^3 )/x) (d/dx)(3x+1)^3 = (d/(d(3x+1)))(3x+1)^3 ×(d/dx)(3x+1) = = 9(3x+1)^2 (d/dx)(5x−1)^3 = (d/(d(5x−1)))(5x−1)^3 ×(d/dx)(5x−1) = = 15(5x−1)^2 ⇒ lim_(x→+0) (9(3x+1)^2 −15(5x−1)^3 ) = 9(1)^2 −15(−1)^3 = 9−(−15) = = 24

$${g}\left({x}\right)\:=\:\begin{cases}{{x}^{\mathrm{2}} }&{{x}\:\geqslant\:\mathrm{1}}\\{{x}^{\mathrm{3}} }&{{x}\:<\:\mathrm{1}}\end{cases} \\ $$ $$\Rightarrow\:\underset{{x}\rightarrow+\mathrm{0}} {\mathrm{lim}}\frac{{g}\left(\mathrm{1}+\mathrm{3}{x}\right)−{g}\left(\mathrm{1}−\mathrm{5}{x}\right)}{{x}}\:= \\ $$ $$=\:\underset{{x}\rightarrow+\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{3}} −\left(\mathrm{5}{x}−\mathrm{1}\right)^{\mathrm{3}} }{{x}} \\ $$ $$\frac{{d}}{{dx}}\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{3}} \:=\:\frac{{d}}{{d}\left(\mathrm{3}{x}+\mathrm{1}\right)}\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{3}} ×\frac{{d}}{{dx}}\left(\mathrm{3}{x}+\mathrm{1}\right)\:= \\ $$ $$=\:\mathrm{9}\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$ $$\frac{{d}}{{dx}}\left(\mathrm{5}{x}−\mathrm{1}\right)^{\mathrm{3}} \:=\:\frac{{d}}{{d}\left(\mathrm{5}{x}−\mathrm{1}\right)}\left(\mathrm{5}{x}−\mathrm{1}\right)^{\mathrm{3}} ×\frac{{d}}{{dx}}\left(\mathrm{5}{x}−\mathrm{1}\right)\:= \\ $$ $$=\:\mathrm{15}\left(\mathrm{5}{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$ $$\Rightarrow\:\underset{{x}\rightarrow+\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{9}\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{15}\left(\mathrm{5}{x}−\mathrm{1}\right)^{\mathrm{3}} \right) \\ $$ $$=\:\mathrm{9}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{15}\left(−\mathrm{1}\right)^{\mathrm{3}} \:=\:\mathrm{9}−\left(−\mathrm{15}\right)\:= \\ $$ $$=\:\mathrm{24} \\ $$

Commented bycortano1 last updated on 08/Mar/22

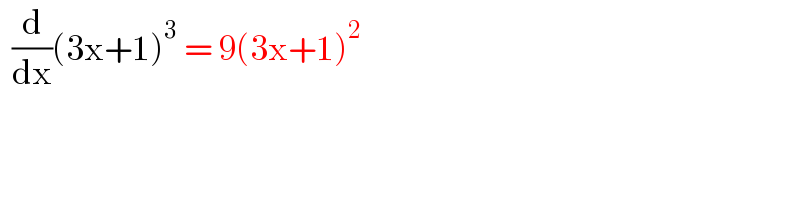
(d/dx)(3x+1)^3 = 9(3x+1)^2

$$\:\:\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{3x}+\mathrm{1}\right)^{\mathrm{3}} \:=\:\mathrm{9}\left(\mathrm{3x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$

Commented byalephzero last updated on 08/Mar/22

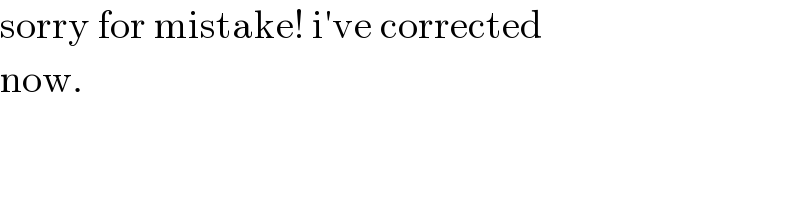
sorry for mistake! i′ve corrected now.

$$\mathrm{sorry}\:\mathrm{for}\:\mathrm{mistake}!\:\mathrm{i}'\mathrm{ve}\:\mathrm{corrected} \\ $$ $$\mathrm{now}. \\ $$

Commented bymr W last updated on 08/Mar/22

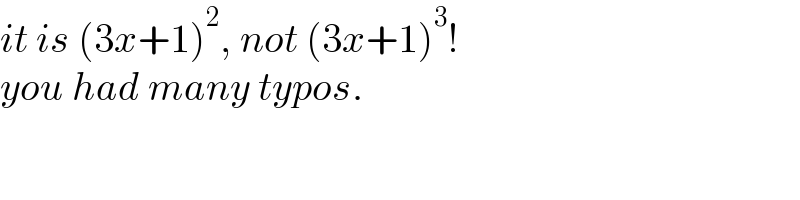
it is (3x+1)^2 , not (3x+1)^3 ! you had many typos.

$${it}\:{is}\:\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} ,\:{not}\:\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{3}} ! \\ $$ $${you}\:{had}\:{many}\:{typos}. \\ $$

Answered by mr W last updated on 07/Mar/22

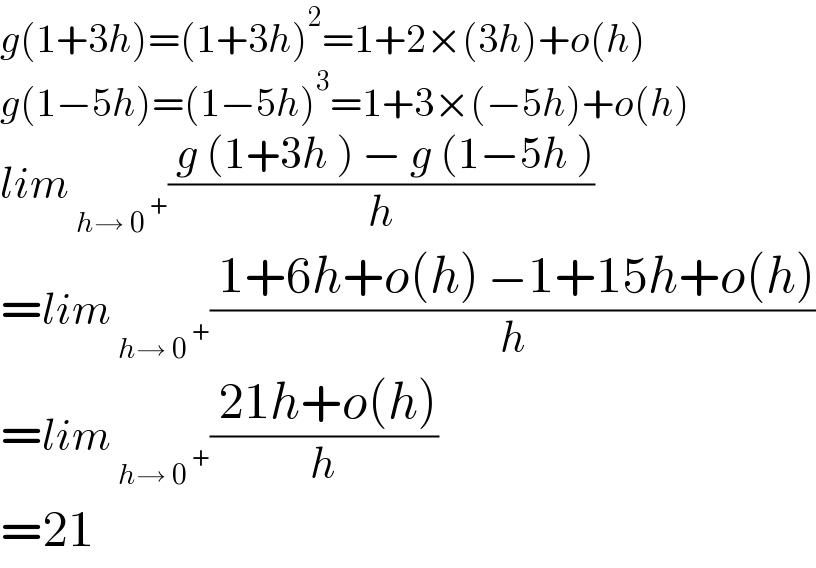
g(1+3h)=(1+3h)^2 =1+2×(3h)+o(h) g(1−5h)=(1−5h)^3 =1+3×(−5h)+o(h) lim_( h→ 0^( +) ) (( g (1+3h ) − g (1−5h ))/h) =lim_( h→ 0^( +) ) (( 1+6h+o(h) −1+15h+o(h))/h) =lim_( h→ 0^( +) ) (( 21h+o(h))/h) =21

$${g}\left(\mathrm{1}+\mathrm{3}{h}\right)=\left(\mathrm{1}+\mathrm{3}{h}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{2}×\left(\mathrm{3}{h}\right)+{o}\left({h}\right) \\ $$ $${g}\left(\mathrm{1}−\mathrm{5}{h}\right)=\left(\mathrm{1}−\mathrm{5}{h}\right)^{\mathrm{3}} =\mathrm{1}+\mathrm{3}×\left(−\mathrm{5}{h}\right)+{o}\left({h}\right) \\ $$ $${lim}_{\:{h}\rightarrow\:\mathrm{0}^{\:+} } \frac{\:{g}\:\left(\mathrm{1}+\mathrm{3}{h}\:\right)\:−\:{g}\:\left(\mathrm{1}−\mathrm{5}{h}\:\right)}{{h}} \\ $$ $$={lim}_{\:{h}\rightarrow\:\mathrm{0}^{\:+} } \frac{\:\mathrm{1}+\mathrm{6}{h}+{o}\left({h}\right)\:−\mathrm{1}+\mathrm{15}{h}+{o}\left({h}\right)}{{h}} \\ $$ $$={lim}_{\:{h}\rightarrow\:\mathrm{0}^{\:+} } \frac{\:\mathrm{21}{h}+{o}\left({h}\right)}{{h}} \\ $$ $$=\mathrm{21} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com