Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 168859 by Shrinava last updated on 19/Apr/22

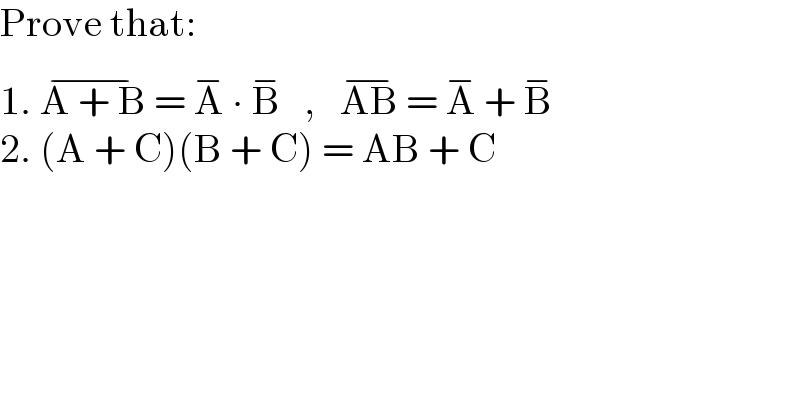
Prove that: 1. A + B^(−) = A^(−) ∙ B^(−) , AB^(−) = A^(−) + B^(−) 2. (A + C)(B + C) = AB + C

$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\mathrm{1}.\:\overline {\mathrm{A}\:+\:\mathrm{B}}\:=\:\overline {\mathrm{A}}\:\centerdot\:\overline {\mathrm{B}}\:\:\:,\:\:\:\overline {\mathrm{AB}}\:=\:\overline {\mathrm{A}}\:+\:\overline {\mathrm{B}} \\ $$$$\mathrm{2}.\:\left(\mathrm{A}\:+\:\mathrm{C}\right)\left(\mathrm{B}\:+\:\mathrm{C}\right)\:=\:\mathrm{AB}\:+\:\mathrm{C} \\ $$

Answered by Rasheed.Sindhi last updated on 19/Apr/22

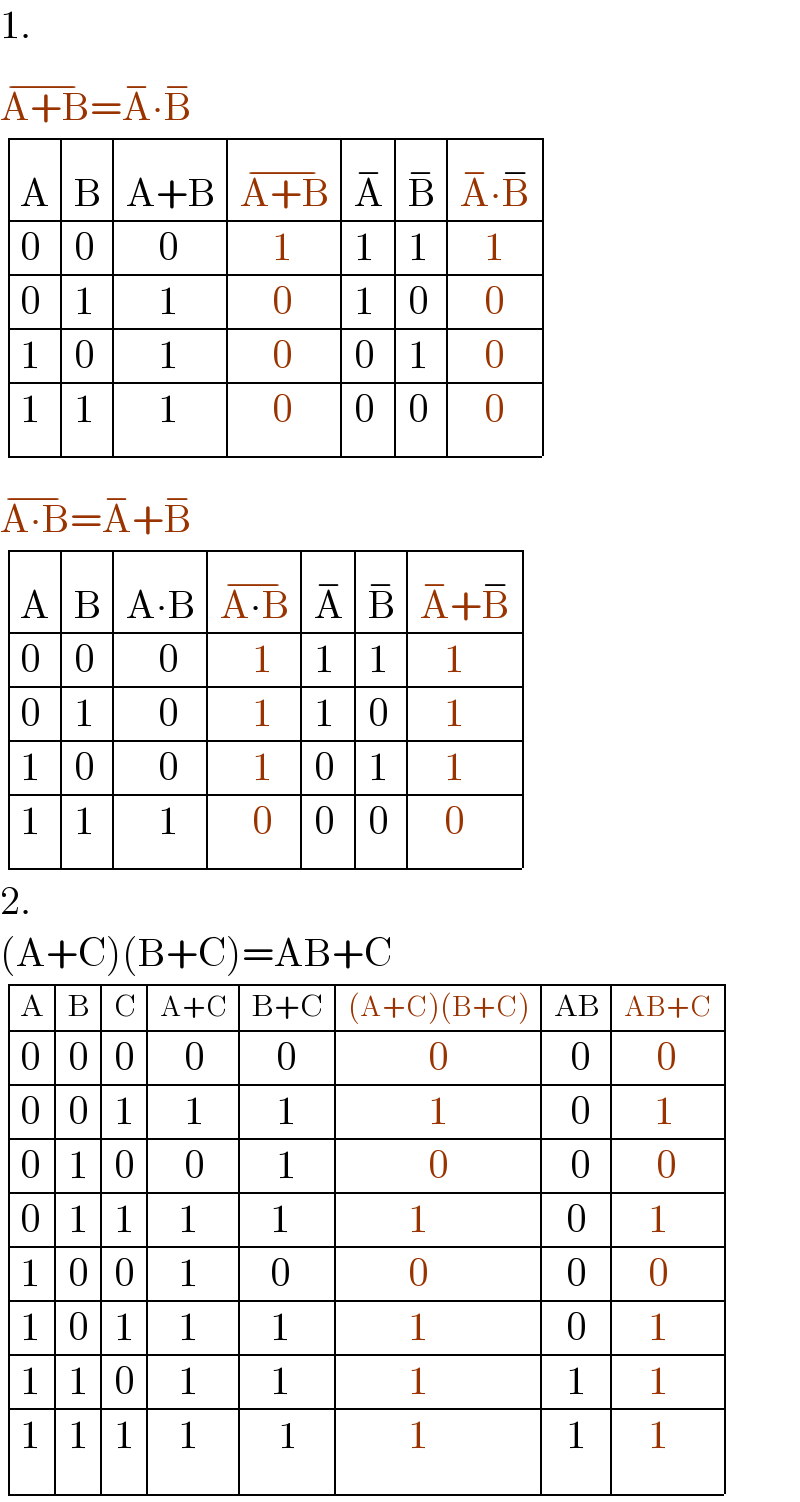
1. A+B^(−) =A^− ∙B^(−) determinant ((A,B,(A+B),(A+B^(−) ),A^− ,B^− ,(A^− ∙B^(−) )),(0,0,( 0),( 1),1,1,( 1)),(0,1,( 1),( 0),1,0,( 0)),(1,0,( 1),( 0),0,1,( 0)),(1,1,( 1),( 0),0,0,( 0))) A∙B^(−) =A^− +B^(−) determinant ((A,B,(A∙B),(A∙B^(−) ),A^− ,B^− ,(A^− +B^(−) )),(0,0,( 0),( 1),1,1,( 1)),(0,1,( 0),( 1),1,0,( 1)),(1,0,( 0),( 1),0,1,( 1)),(1,1,( 1),( 0),0,0,( 0))) 2. (A+C)(B+C)=AB+C determinant ((A,B,C,(A+C),(B+C),((A+C)(B+C)),(AB),(AB+C)),(0,0,0,( 0),( 0),( 0),( 0),( 0)),(0,0,1,( 1),( 1),( 1),( 0),( 1)),(0,1,0,( 0),( 1),( 0),( 0),( 0)),(0,1,1,( 1),( 1),( 1),( 0),( 1)),(1,0,0,( 1),( 0),( 0),( 0),( 0)),(1,0,1,( 1),( 1),( 1),( 0),( 1)),(1,1,0,( 1),( 1),( 1),( 1),( 1)),(1,1,1,( 1),( 1),( 1),( 1),( 1)))

$$\mathrm{1}. \\ $$$$\overline {\mathrm{A}+\mathrm{B}}=\overset{−} {\mathrm{A}}\centerdot\overline {\mathrm{B}} \\ $$$$\begin{array}{|c|c|c|c|c|}{\mathrm{A}}&\hline{\mathrm{B}}&\hline{\mathrm{A}+\mathrm{B}}&\hline{\overline {\mathrm{A}+\mathrm{B}}}&\hline{\overset{−} {\mathrm{A}}}&\hline{\overset{−} {\mathrm{B}}}&\hline{\overset{−} {\mathrm{A}}\centerdot\overline {\mathrm{B}}}\\{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\:\:\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\:\:\:\mathrm{1}}\\{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\:\:\:\:\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\:\:\:\mathrm{0}}\\{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\:\:\:\:\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\:\:\:\mathrm{0}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\:\:\:\:\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\:\:\:\mathrm{0}}\\\hline\end{array}\: \\ $$$$\overline {\mathrm{A}\centerdot\mathrm{B}}=\overset{−} {\mathrm{A}}+\overline {\mathrm{B}} \\ $$$$\begin{array}{|c|c|c|c|c|}{\mathrm{A}}&\hline{\mathrm{B}}&\hline{\mathrm{A}\centerdot\mathrm{B}}&\hline{\overline {\mathrm{A}\centerdot\mathrm{B}}}&\hline{\overset{−} {\mathrm{A}}}&\hline{\overset{−} {\mathrm{B}}}&\hline{\overset{−} {\mathrm{A}}+\overline {\mathrm{B}}}\\{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\:\:\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\:\:\:\mathrm{1}}\\{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\:\:\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\:\:\:\mathrm{1}}\\{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\:\:\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\:\:\:\mathrm{1}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\:\:\:\:\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\:\:\:\mathrm{0}}\\\hline\end{array}\: \\ $$$$\mathrm{2}. \\ $$$$\left(\mathrm{A}+\mathrm{C}\right)\left(\mathrm{B}+\mathrm{C}\right)=\mathrm{AB}+\mathrm{C}\: \\ $$$$\begin{array}{|c|c|c|c|c|c|c|c|c|}{\mathrm{A}}&\hline{\mathrm{B}}&\hline{\mathrm{C}}&\hline{\mathrm{A}+\mathrm{C}}&\hline{\mathrm{B}+\mathrm{C}}&\hline{\left(\mathrm{A}+\mathrm{C}\right)\left(\mathrm{B}+\mathrm{C}\right)}&\hline{\mathrm{AB}}&\hline{\mathrm{AB}+\mathrm{C}}\\{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\:\:\:\mathrm{0}}&\hline{\:\:\:\mathrm{0}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{0}}&\hline{\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{0}}\\{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{1}}&\hline{\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{1}}\\{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\:\:\:\mathrm{0}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{0}}&\hline{\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{0}}\\{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{1}}&\hline{\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{1}}\\{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\mathrm{0}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{0}}&\hline{\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{0}}\\{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{1}}&\hline{\:\:\mathrm{0}}&\hline{\:\:\:\:\mathrm{1}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{1}}&\hline{\:\:\mathrm{1}}&\hline{\:\:\:\:\mathrm{1}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\:\:\:\mathrm{1}}&\hline{\:\:\:\:\mathrm{1}}&\hline{\:\:\:\:\:\:\:\:\:\:\mathrm{1}}&\hline{\:\:\mathrm{1}}&\hline{\:\:\:\:\mathrm{1}}\\\hline\end{array} \\ $$

Commented by Shrinava last updated on 19/Apr/22

perfect thankyou sir

$$\mathrm{perfect}\:\mathrm{thankyou}\:\boldsymbol{\mathrm{sir}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com