
Question Number 17086 by Joel577 last updated on 30/Jun/17

$$\underset{−\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{dx} \\ $$
Commented by Joel577 last updated on 30/Jun/17
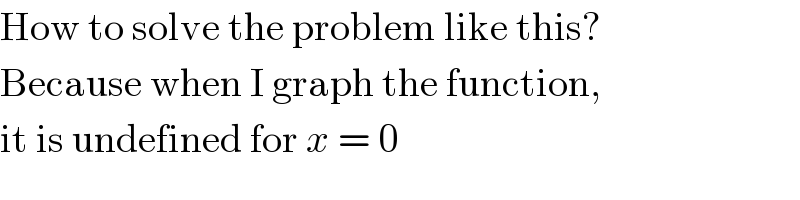
$$\mathrm{How}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{like}\:\mathrm{this}? \\ $$$$\mathrm{Because}\:\mathrm{when}\:\mathrm{I}\:\mathrm{graph}\:\mathrm{the}\:\mathrm{function}, \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{undefined}\:\mathrm{for}\:{x}\:=\:\mathrm{0} \\ $$
Commented by Joel577 last updated on 30/Jun/17

$$\mathrm{Is}\:\mathrm{it}\:−\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{or}\:\infty\:? \\ $$
Commented by ajfour last updated on 30/Jun/17

$$\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is}\:\infty. \\ $$
Commented by ajfour last updated on 30/Jun/17
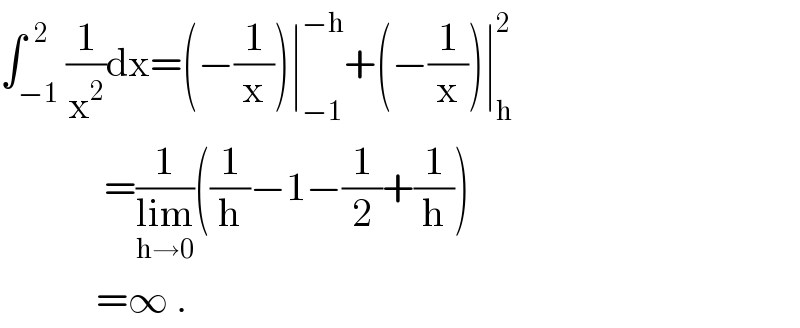
$$\int_{−\mathrm{1}} ^{\:\:\mathrm{2}} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\left(−\frac{\mathrm{1}}{\mathrm{x}}\right)\mid_{−\mathrm{1}} ^{−\mathrm{h}} +\left(−\frac{\mathrm{1}}{\mathrm{x}}\right)\mid_{\mathrm{h}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}}\left(\frac{\mathrm{1}}{\mathrm{h}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{h}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\infty\:. \\ $$
Commented by Joel577 last updated on 01/Jul/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by 1234Hello last updated on 04/Jul/17

$$\mathrm{But}\:\mathrm{it}\:\mathrm{can}\:\mathrm{also}\:\mathrm{be}\:\mathrm{checked}\:\mathrm{that}\:\int\frac{{dx}}{{x}^{\mathrm{2}} } \\ $$$$=\:\frac{−\mathrm{1}}{{x}}\:\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{at}\:{x}\:=\:\mathrm{0}. \\ $$
Answered by prakash jain last updated on 30/Jun/17
![It is an improper integral. 2 types of improper integral 1. ∫_a ^b f(x)dx and either a and/or b is unbouned (−∞ or +∞) 2. ∫_a ^b f(x)dx where f(x) is unbounded at one or more value in [a,b]. Then we need to split the integral. ∫_a ^b f(x)dx=∫_a ^c f(x)dx+∫_c ^b f(x)dx c∈[a,b] and f(c) is umbounded. in question f(x)=(1/x^2 ) f(x) is unbouned at x=0 ∫_(−1) ^2 (1/x^2 )dx is convergent only if ∫_(−1) ^0 (1/x^2 )dx , ∫_0 ^2 (1/x^2 )dx are convergent. if any of the split integral does not converge the combined integral does not converge. ∫_(−1) ^0 (1/x^2 )dx does not converge. so ∫_(−1) ^2 (1/x^2 )dx does not converge. ∫_(−1) ^2 (1/x^2 )dx integral is divergent.](Q17103.png)
$$\mathrm{It}\:\mathrm{is}\:\mathrm{an}\:\mathrm{improper}\:\mathrm{integral}. \\ $$$$\mathrm{2}\:\mathrm{types}\:\mathrm{of}\:\mathrm{improper}\:\mathrm{integral} \\ $$$$\mathrm{1}.\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}\:\mathrm{and}\:\mathrm{either}\:{a}\:{and}/{or}\:{b} \\ $$$$\mathrm{is}\:\mathrm{unbouned}\:\left(−\infty\:\mathrm{or}\:+\infty\right) \\ $$$$\mathrm{2}.\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}\:\mathrm{where}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{unbounded} \\ $$$$\mathrm{at}\:\mathrm{one}\:\mathrm{or}\:\mathrm{more}\:\mathrm{value}\:\mathrm{in}\:\left[{a},{b}\right].\:\mathrm{Then} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{split}\:\mathrm{the}\:\mathrm{integral}. \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{c}} {f}\left({x}\right){dx}+\int_{{c}} ^{{b}} {f}\left({x}\right){dx} \\ $$$${c}\in\left[{a},{b}\right]\:\mathrm{and}\:{f}\left({c}\right)\:\mathrm{is}\:\mathrm{umbounded}. \\ $$$$\mathrm{in}\:\mathrm{question}\:{f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{unbouned}\:\mathrm{at}\:{x}=\mathrm{0} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{only}\:\mathrm{if} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\:,\:\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\:\mathrm{are}\:\mathrm{convergent}. \\ $$$$\mathrm{if}\:\mathrm{any}\:\mathrm{of}\:\mathrm{the}\:\mathrm{split}\:\mathrm{integral}\:\mathrm{does} \\ $$$$\mathrm{not}\:\mathrm{converge}\:\mathrm{the}\:\mathrm{combined} \\ $$$$\mathrm{integral}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}. \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}. \\ $$$$\mathrm{so}\:\int_{−\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\:\mathrm{does}\:\mathrm{not}\:\mathrm{converge}. \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{divergent}. \\ $$
Commented by Joel577 last updated on 01/Jul/17
$${thank}\:{you}\:{very}\:{much} \\ $$
