
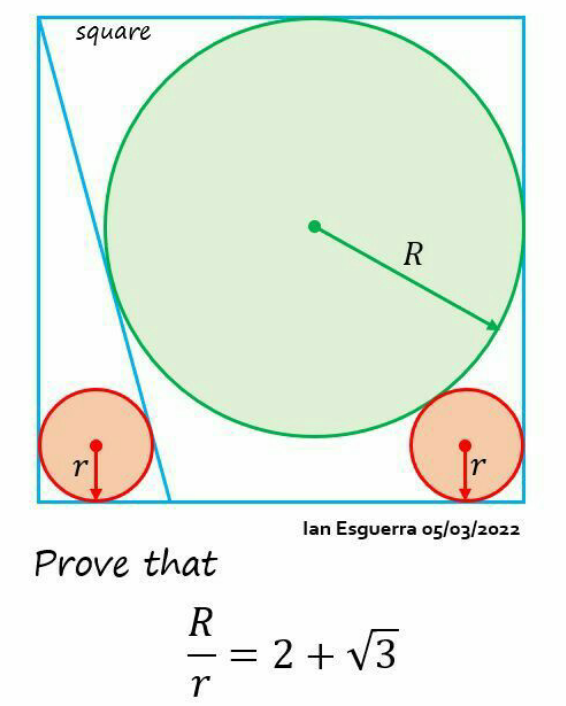
Question Number 172763 by mnjuly1970 last updated on 01/Jul/22
Answered by aleks041103 last updated on 01/Jul/22
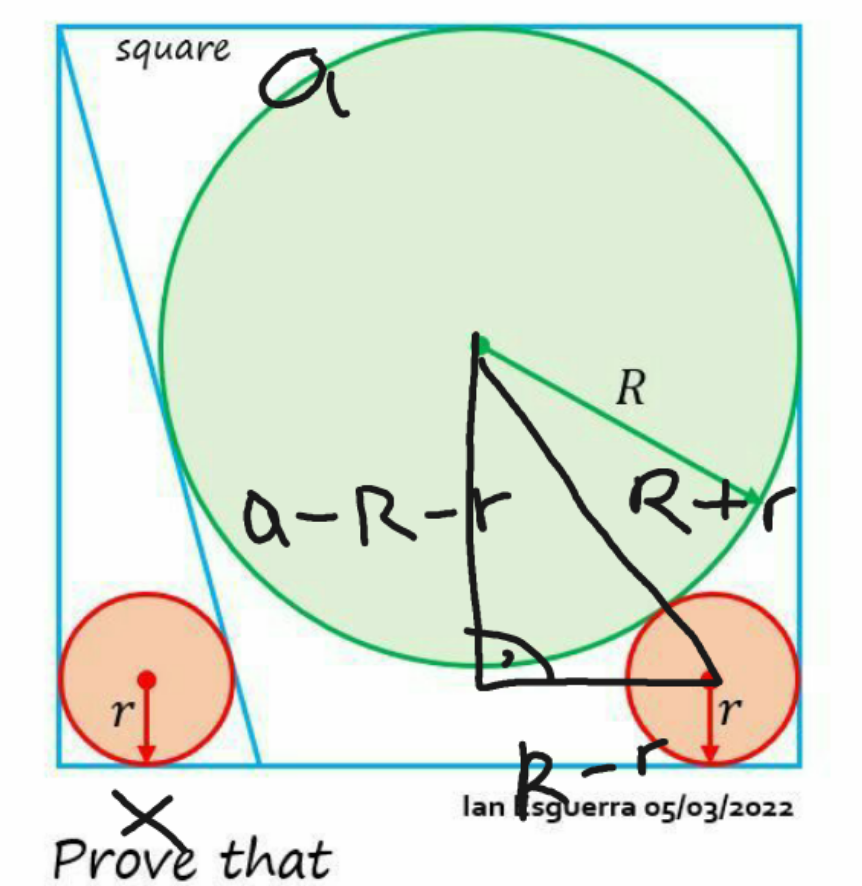
Commented by aleks041103 last updated on 01/Jul/22
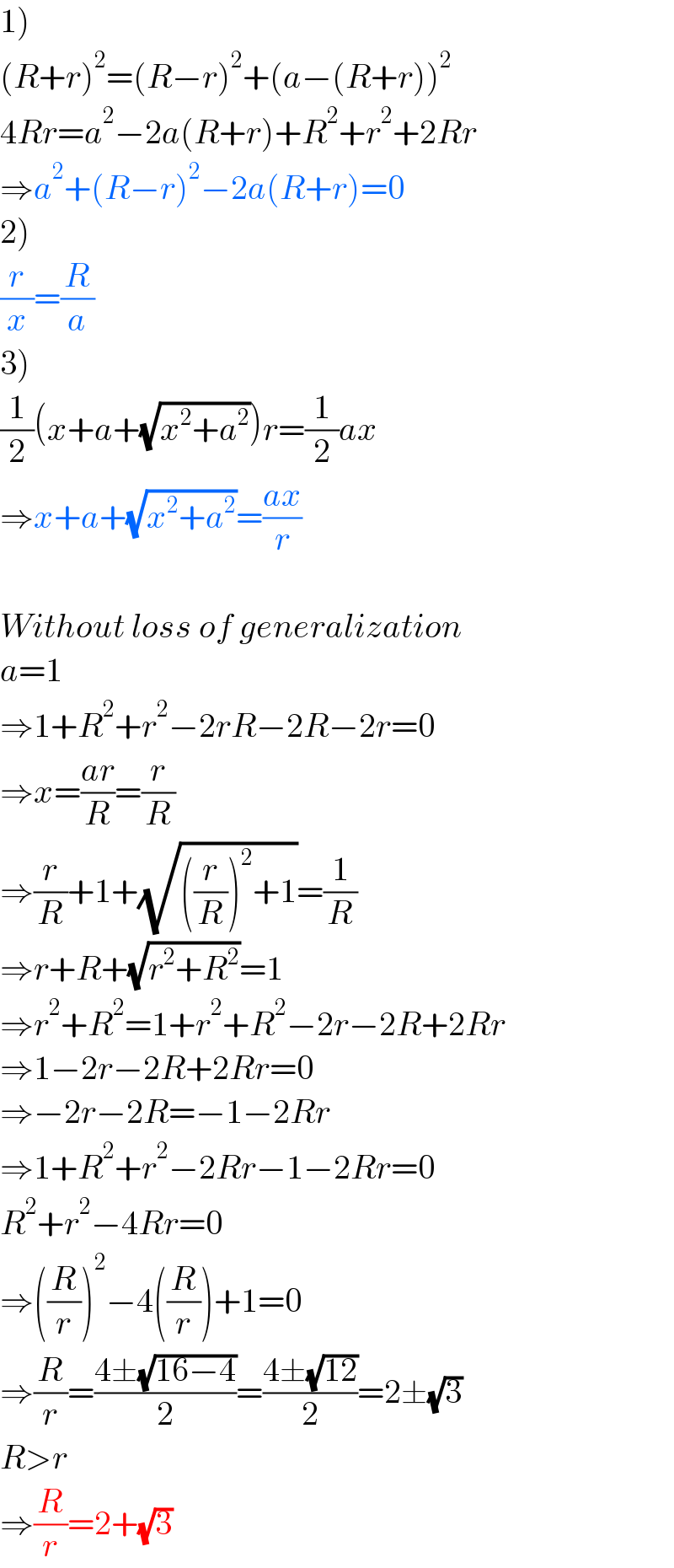
$$\left.\mathrm{1}\right) \\ $$$$\left({R}+{r}\right)^{\mathrm{2}} =\left({R}−{r}\right)^{\mathrm{2}} +\left({a}−\left({R}+{r}\right)\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{Rr}={a}^{\mathrm{2}} −\mathrm{2}{a}\left({R}+{r}\right)+{R}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{2}{Rr} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +\left({R}−{r}\right)^{\mathrm{2}} −\mathrm{2}{a}\left({R}+{r}\right)=\mathrm{0} \\ $$$$\left.\mathrm{2}\right) \\ $$$$\frac{{r}}{{x}}=\frac{{R}}{{a}} \\ $$$$\left.\mathrm{3}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{a}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\right){r}=\frac{\mathrm{1}}{\mathrm{2}}{ax} \\ $$$$\Rightarrow{x}+{a}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }=\frac{{ax}}{{r}} \\ $$$$ \\ $$$${Without}\:{loss}\:{of}\:{generalization} \\ $$$${a}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}+{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{rR}−\mathrm{2}{R}−\mathrm{2}{r}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{{ar}}{{R}}=\frac{{r}}{{R}} \\ $$$$\Rightarrow\frac{{r}}{{R}}+\mathrm{1}+\sqrt{\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{R}} \\ $$$$\Rightarrow{r}+{R}+\sqrt{{r}^{\mathrm{2}} +{R}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{r}^{\mathrm{2}} +{R}^{\mathrm{2}} =\mathrm{1}+{r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{r}−\mathrm{2}{R}+\mathrm{2}{Rr} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2}{r}−\mathrm{2}{R}+\mathrm{2}{Rr}=\mathrm{0} \\ $$$$\Rightarrow−\mathrm{2}{r}−\mathrm{2}{R}=−\mathrm{1}−\mathrm{2}{Rr} \\ $$$$\Rightarrow\mathrm{1}+{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rr}−\mathrm{1}−\mathrm{2}{Rr}=\mathrm{0} \\ $$$${R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{4}{Rr}=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{{R}}{{r}}\right)^{\mathrm{2}} −\mathrm{4}\left(\frac{{R}}{{r}}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\frac{{R}}{{r}}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{4}\pm\sqrt{\mathrm{12}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$${R}>{r} \\ $$$$\Rightarrow\frac{{R}}{{r}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$
Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 01/Jul/22
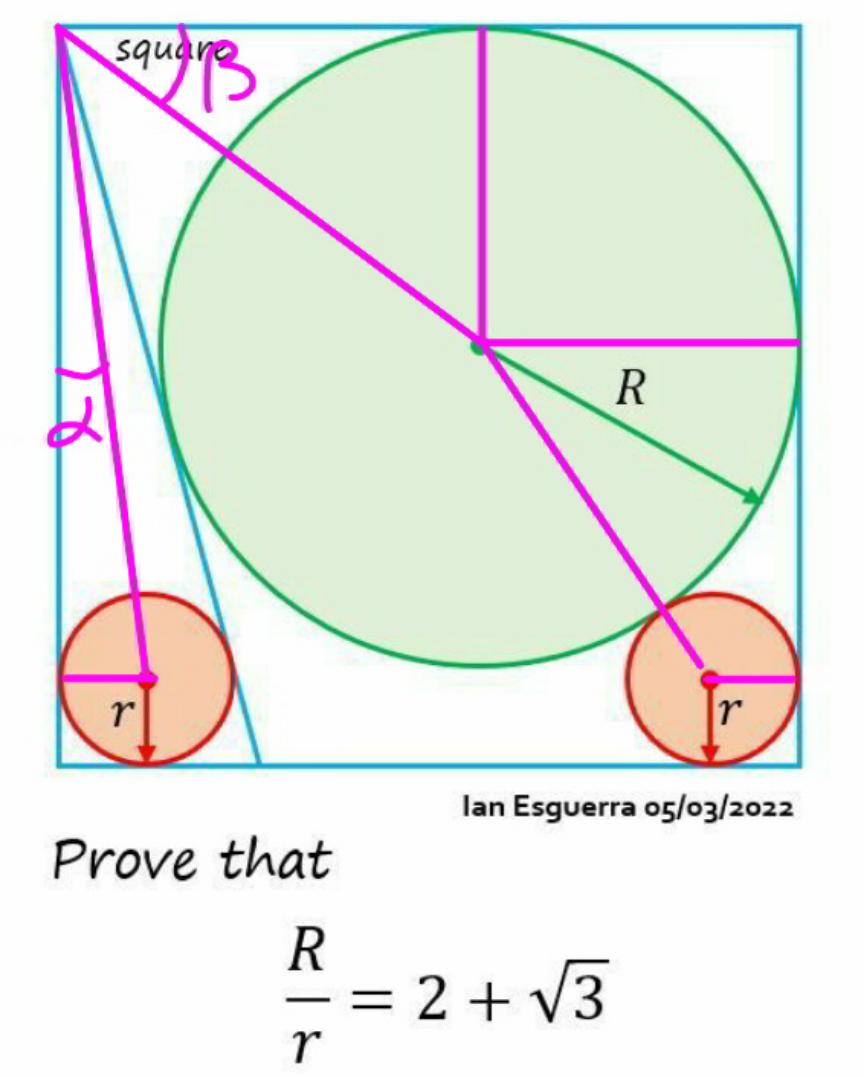
Commented by mr W last updated on 01/Jul/22
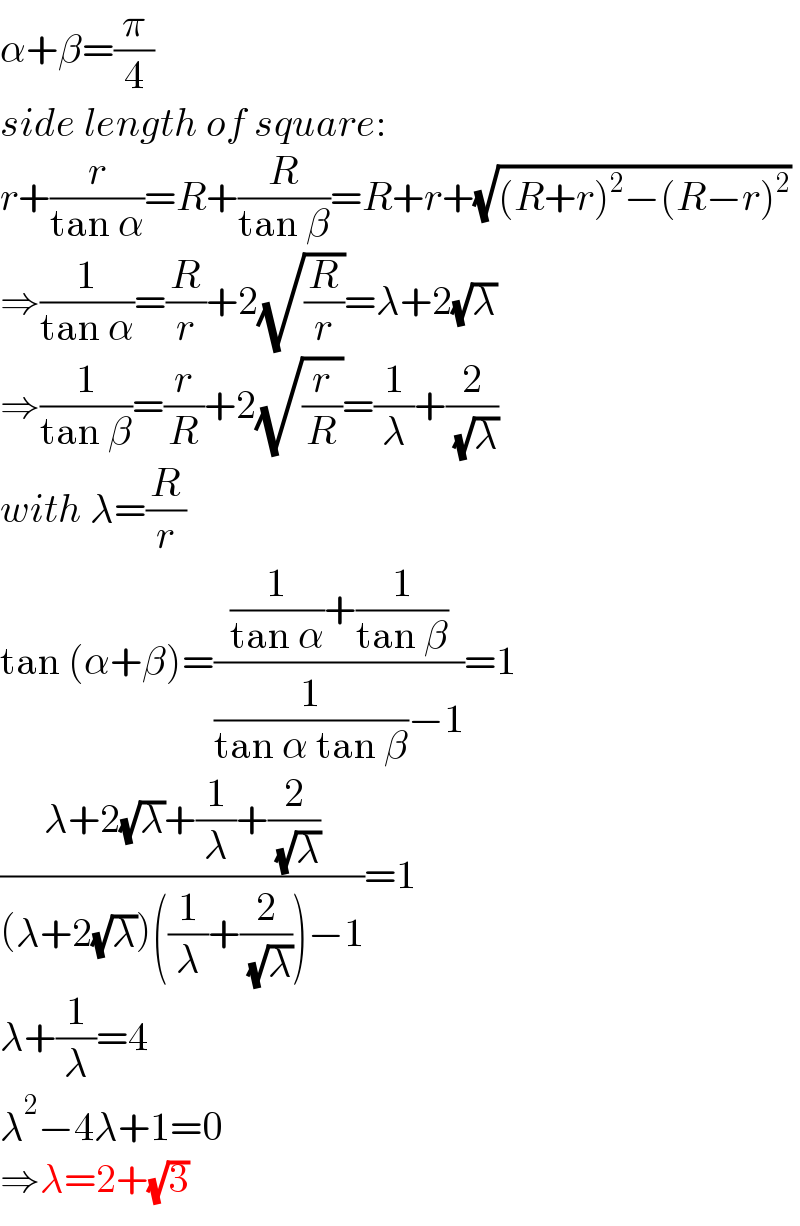
$$\alpha+\beta=\frac{\pi}{\mathrm{4}} \\ $$$${side}\:{length}\:{of}\:{square}: \\ $$$${r}+\frac{{r}}{\mathrm{tan}\:\alpha}={R}+\frac{{R}}{\mathrm{tan}\:\beta}={R}+{r}+\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}=\frac{{R}}{{r}}+\mathrm{2}\sqrt{\frac{{R}}{{r}}}=\lambda+\mathrm{2}\sqrt{\lambda} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\beta}=\frac{{r}}{{R}}+\mathrm{2}\sqrt{\frac{{r}}{{R}}}=\frac{\mathrm{1}}{\lambda}+\frac{\mathrm{2}}{\:\sqrt{\lambda}} \\ $$$${with}\:\lambda=\frac{{R}}{{r}} \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}+\frac{\mathrm{1}}{\mathrm{tan}\:\beta}}{\frac{\mathrm{1}}{\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta}−\mathrm{1}}=\mathrm{1} \\ $$$$\frac{\lambda+\mathrm{2}\sqrt{\lambda}+\frac{\mathrm{1}}{\lambda}+\frac{\mathrm{2}}{\:\sqrt{\lambda}}}{\left(\lambda+\mathrm{2}\sqrt{\lambda}\right)\left(\frac{\mathrm{1}}{\lambda}+\frac{\mathrm{2}}{\:\sqrt{\lambda}}\right)−\mathrm{1}}=\mathrm{1} \\ $$$$\lambda+\frac{\mathrm{1}}{\lambda}=\mathrm{4} \\ $$$$\lambda^{\mathrm{2}} −\mathrm{4}\lambda+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 01/Jul/22
$$\mathrm{peace}\:\mathrm{be}\:\mathrm{upon}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 01/Jul/22
$${the}\:{same}\:{to}\:{you}\:{sir}! \\ $$
Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
