
Previous in Relation and Functions Next in Relation and Functions
Question Number 173132 by alcohol last updated on 07/Jul/22
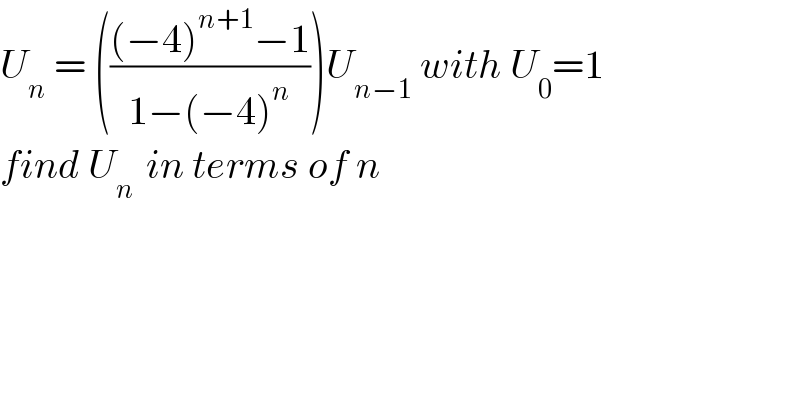
$${U}_{{n}} \:=\:\left(\frac{\left(−\mathrm{4}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{1}−\left(−\mathrm{4}\right)^{{n}} }\right){U}_{{n}−\mathrm{1}} \:{with}\:{U}_{\mathrm{0}} =\mathrm{1} \\ $$$${find}\:{U}_{{n}\:} \:{in}\:{terms}\:{of}\:{n}\:\: \\ $$
Commented by kaivan.ahmadi last updated on 07/Jul/22
![we have (u_n /u_(n−1) )=(((−4)^(n+1) −1)/(1−(−4)^n )) on the other hand u_1 =(((16−1)/(1+4)))1=3 u_2 =(((−64−1)/(1−16)))3=13 u_3 =(((256−1)/(1+64)))13=51 u_4 =(((−1024−1)/(1−256)))51=205 determinant (((n 1 2 3 4 )),(( 4×1−1 4×3+1 4×13−1 4×51+1 )),((u_n 3 13 51 205))) so u_n =4u_(n−1) +(−1)^n ⇒(u_n /u_(n−1) )=4+(((−1)^n )/u_(n−1) )⇒(((−4)^(n+1) −1)/(1−(−4)^n ))=4+(((−1)^n )/u_(n−1) ) ⇒(((−4)^(n+1) −1)/(1−(−4)^n ))−4=(((−1)^n )/u_(n−1) )⇒ (((−4)^(n+1) −1−4−(−4)^(n+1) )/(1−(−4)^n ))=(((−1)^n )/u_(n−1) ) ⇒((−5)/(1−(−4)^n ))=(((−1)^n )/u_(n−1) )⇒u_(n−1) =(((−1)^n [(−4)^n −1])/5) replace n with n+1 u_n =(((−1)^(n+1) [(−4)^(n+1) −1])/5)](Q173137.png)
$${we}\:{have}\:\frac{{u}_{{n}} }{{u}_{{n}−\mathrm{1}} }=\frac{\left(−\mathrm{4}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{1}−\left(−\mathrm{4}\right)^{{n}} } \\ $$$${on}\:{the}\:{other}\:{hand} \\ $$$${u}_{\mathrm{1}} =\left(\frac{\mathrm{16}−\mathrm{1}}{\mathrm{1}+\mathrm{4}}\right)\mathrm{1}=\mathrm{3} \\ $$$${u}_{\mathrm{2}} =\left(\frac{−\mathrm{64}−\mathrm{1}}{\mathrm{1}−\mathrm{16}}\right)\mathrm{3}=\mathrm{13} \\ $$$${u}_{\mathrm{3}} =\left(\frac{\mathrm{256}−\mathrm{1}}{\mathrm{1}+\mathrm{64}}\right)\mathrm{13}=\mathrm{51} \\ $$$${u}_{\mathrm{4}} =\left(\frac{−\mathrm{1024}−\mathrm{1}}{\mathrm{1}−\mathrm{256}}\right)\mathrm{51}=\mathrm{205} \\ $$$$\begin{array}{|c|c|c|}{{n}\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:}\\{\:\:\:\:\:\:\:\mathrm{4}×\mathrm{1}−\mathrm{1}\:\:\:\:\:\:\:\mathrm{4}×\mathrm{3}+\mathrm{1}\:\:\:\:\:\mathrm{4}×\mathrm{13}−\mathrm{1}\:\:\:\:\:\:\mathrm{4}×\mathrm{51}+\mathrm{1}\:}\\{{u}_{{n}} \:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{13}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{51}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{205}}\\\hline\end{array} \\ $$$${so}\:{u}_{{n}} =\mathrm{4}{u}_{{n}−\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} \\ $$$$\Rightarrow\frac{{u}_{{n}} }{{u}_{{n}−\mathrm{1}} }=\mathrm{4}+\frac{\left(−\mathrm{1}\right)^{{n}} }{{u}_{{n}−\mathrm{1}} }\Rightarrow\frac{\left(−\mathrm{4}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{1}−\left(−\mathrm{4}\right)^{{n}} }=\mathrm{4}+\frac{\left(−\mathrm{1}\right)^{{n}} }{{u}_{{n}−\mathrm{1}} } \\ $$$$\Rightarrow\frac{\left(−\mathrm{4}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{1}−\left(−\mathrm{4}\right)^{{n}} }−\mathrm{4}=\frac{\left(−\mathrm{1}\right)^{{n}} }{{u}_{{n}−\mathrm{1}} }\Rightarrow \\ $$$$\frac{\left(−\mathrm{4}\right)^{{n}+\mathrm{1}} −\mathrm{1}−\mathrm{4}−\left(−\mathrm{4}\right)^{{n}+\mathrm{1}} }{\mathrm{1}−\left(−\mathrm{4}\right)^{{n}} }=\frac{\left(−\mathrm{1}\right)^{{n}} }{{u}_{{n}−\mathrm{1}} } \\ $$$$\Rightarrow\frac{−\mathrm{5}}{\mathrm{1}−\left(−\mathrm{4}\right)^{{n}} }=\frac{\left(−\mathrm{1}\right)^{{n}} }{{u}_{{n}−\mathrm{1}} }\Rightarrow{u}_{{n}−\mathrm{1}} =\frac{\left(−\mathrm{1}\right)^{{n}} \left[\left(−\mathrm{4}\right)^{{n}} −\mathrm{1}\right]}{\mathrm{5}} \\ $$$${replace}\:{n}\:{with}\:{n}+\mathrm{1} \\ $$$${u}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left[\left(−\mathrm{4}\right)^{{n}+\mathrm{1}} −\mathrm{1}\right]}{\mathrm{5}} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 07/Jul/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by kaivan.ahmadi last updated on 07/Jul/22
$${thank}\:{you}\:{so}\:{much} \\ $$
Commented by mr W last updated on 06/Jan/23

$${thanks}\:{sir}! \\ $$$${your}\:{answer}\:{is}\:{correct},\:{but}\:{solution} \\ $$$${is}\:{not}\:{mathematically}\:{strict}. \\ $$$${you}\:{calculated}\:{some}\:{values}\:{for}\:{a}_{{n}} : \\ $$$${a}_{\mathrm{1}} =\mathrm{3},\:{a}_{\mathrm{2}} =\mathrm{13},\:{a}_{\mathrm{3}} =\mathrm{51},\:{a}_{\mathrm{4}} =\mathrm{205}, \\ $$$${and}\:{then}\:{say}\:{u}_{{n}} =\mathrm{4}{u}_{{n}−\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} . \\ $$$${this}\:{method}\:{is}\:{not}\:{mathematically} \\ $$$${strict}.\:{it}'{s}\:{sometimes}\:{a}\:{matter}\:{of} \\ $$$${luck}\:{that}\:{we}\:``{guess}''\:{the}\:{right}\: \\ $$$${answer}.\:{a}\:{famous}\:{example}: \\ $$$${a}_{\mathrm{1}} =\mathrm{1},\:{a}_{\mathrm{2}} =\mathrm{2},\:{a}_{\mathrm{3}} =\mathrm{4},\:{a}_{\mathrm{4}} =\mathrm{8},\:{a}_{\mathrm{5}} =\mathrm{16},\:... \\ $$$${it}'{s}\:{the}\:{largest}\:{number}\:{of}\:{portions} \\ $$$${of}\:{a}\:{circle}\:{which}\:{can}\:{be}\:{divided}\:{by}\:{n} \\ $$$${points}\:{on}\:{the}\:{circle}.\:{can}\:{we}\:{say}\:{from} \\ $$$${these}\:{values}\:{that}\:{a}_{{n}} =\mathrm{2}^{{n}−\mathrm{1}} ? \\ $$$${unfortunately}\:{no}!\:{even}\:{it}\:{delivers}\:{the} \\ $$$${correct}\:{values}\:{for}\:{the}\:{first}\:\mathrm{5}\:{cases}. \\ $$$${the}\:{correct}\:{formula}\:{is}\:{a}_{{n}} ={C}_{\mathrm{4}} ^{{n}} +{C}_{\mathrm{2}} ^{{n}} +\mathrm{1}. \\ $$$${this}\:{example}\:{shows}\:{how}\:{dangerous} \\ $$$${it}\:{is}\:{when}\:{we}\:{just}\:{look}\:{at}\:{some} \\ $$$${first}\:{values}\:{and}\:{then}\:{guess}\:{a} \\ $$$${general}\:{formula}\:{for}\:{the}\:{n}^{{th}} \:{term}. \\ $$$${if}\:{you}\:{are}\:{interested},\:{you}\:{may}\:{read} \\ $$$${more}\:{about}\:{this}\:{example}\:{in}\:{Q}\mathrm{180457}. \\ $$
Commented by mr W last updated on 06/Jan/23

$${a}\:{mathematically}\:{strict}\:{solution}\: \\ $$$${for}\:{this}\:{question}\:{see}\:{Q}\mathrm{184401}. \\ $$
