Solve over integer a^3 +2a^2 +3a+4=b!+c!


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 173556 by dragan91 last updated on 13/Jul/22

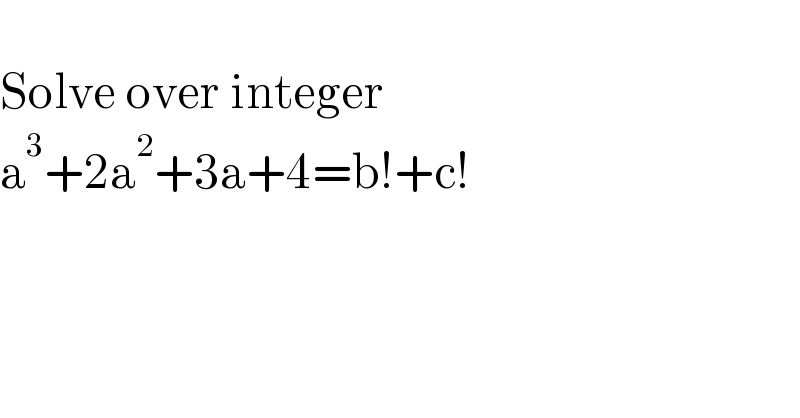
$$ \\ $$$$\mathrm{Solve}\:\mathrm{over}\:\mathrm{integer} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{4}=\mathrm{b}!+\mathrm{c}! \\ $$
	Answered by Rasheed.Sindhi last updated on 14/Jul/22

	$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{4}=\mathrm{b}!+\mathrm{c}! \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{4}−\left(\mathrm{b}!+\mathrm{c}!\right)=\mathrm{0} \\ $$$$\mathcal{T}{he}\:{equation}\:{is}\:{cubic} \\ $$$$\therefore\:\mathrm{a}\:\mathrm{has}\:\mathrm{at}\:\mathrm{most}\:\mathrm{3}\:\mathrm{integral}\:\mathrm{values} \\ $$$${for}\:{particular}\:{value}\:{of}\:{b}\:\&\:{c}.\: \\ $$$$\mathrm{Let}\:\alpha,\beta\:\&\:\gamma\:\:{are}\:{the}\:{roots}\:{of}\:{the}\:{above}\:{equation}. \\ $$$$\alpha+\beta+\gamma=−\mathrm{2}\:,\:\alpha\beta+\beta\gamma+\gamma\alpha=\mathrm{3}\:, \\ $$$$\alpha\beta\gamma=\:\mathrm{b}!+\mathrm{c}!−\mathrm{4} \\ $$$$..... \\ $$$$.... \\ $$
	Commented by dragan91 last updated on 16/Jul/22
	$a^3 +2a^2 +3a+4=b!+c! (a+1)(a^2 +a+2)=b!+c!−2 since b!+c!−2≥0 ∀b,c∈N ⇒(a+1)(a^2 +a+2)≥0⇒a≥−1 a^3 +2a^2 +3a+4 is never divisible by 3 then for 3≤b≤c and b!+c!=3 is no solution a^3 +2a^2 +3a+4 could have solutions for 1+c! (c≠2) or 2+c! (c≠1) We have to consider cases: I)for fixed b!=1⇒b=0=1 c≠2 a)assume a≤c⇒c!≡0(mod a) a^3 +2a^2 +3a+4=1+c! a^3 +2a^2 +3a+3=c! /:a a^2 +2a+3+^ (3/a)=((c!)/a) LHS is integer for a={(−1,1,2,3)} ⇒(a,b,c)={(−1,0,0),(−1,1,0),(−1,0,1) (−1,1,1),(2,4,2),(2,2,4)} b)assume c<a c!<a! a^3 +2a^2 +3a+3<a! its true for a≥6 for a≥6 let a=6+k (k≥0) (6+k)^3 +2(6+k)^2 +3(6+k)+3=c! k^3 +20k^2 +35k+309=c! LHS is not divisible by 2 for any inter ⇒ c=0 or c=1 ⇒k=−7 is no solution (k≥0) c)a=0 no solution II)For fixed b!=2⇒b=2 a^3 +2a^2 +3a+2=c! a)c≥a ⇒c!≡0(mod a) a^3 +2a^2 +3a+2=c!/:a a^2 +2a+3a+(2/a)=((c!)/a) LHS is integer for a={(−1,1,2)} which is already checked solutions b)c<a a^3 +2a^2 +3a+2<a! its true for a≥6⇒a=6+p p≥0 c<6+p (6+p)^3 +2(6+p)^2 +3(6+p)+2=c! p^3 +20p^2 +135p+308=c! p^3 +3p^2 ∙7+3p∙49+343−(p^2 +12p+35)=c! (p+7)^3 −(p+7)(p+5)=c! p+7=t t^3 −t(t−2)=c! Since c<p+6⇒c<t−1<t for t>1 c≢0(mod t)⇒c!≢0(mod t) t^3 −t(t−2)≡0(mod t) its only possible solution for t=1 c!=1^3 −1^2 +2⇒c=2 Its contradiction since c<t−1 c)a=0⇒c=2 (a,b,c)={(0,2,2)} All solutions (a,b,c)={(−1,0,0),(−1,0,1),(−1,1,0), (−1,1,1),(0,2,2),(2,2,4),(2,4,2)}$
	$$ \\ $$$$\underline{\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{4}=\mathrm{b}!+\mathrm{c}!} \\ $$$$\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{a}^{\mathrm{2}} +\mathrm{a}+\mathrm{2}\right)=\mathrm{b}!+\mathrm{c}!−\mathrm{2} \\ $$$$\mathrm{since}\:\mathrm{b}!+\mathrm{c}!−\mathrm{2}\geqslant\mathrm{0}\:\forall\mathrm{b},\mathrm{c}\in\mathbb{N} \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{a}^{\mathrm{2}} +\mathrm{a}+\mathrm{2}\right)\geqslant\mathrm{0}\Rightarrow\mathrm{a}\geqslant−\mathrm{1} \\ $$$$\:\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{4}\:\mathrm{is}\:\mathrm{never}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3} \\ $$$$\mathrm{then}\:\mathrm{for}\:\mathrm{3}\leqslant\mathrm{b}\leqslant\mathrm{c}\:\mathrm{and}\:\mathrm{b}!+\mathrm{c}!=\mathrm{3}\: \\ $$$$\mathrm{is}\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{4}\:\mathrm{could}\:\mathrm{have}\:\mathrm{solutions} \\ $$$$\mathrm{for}\:\:\mathrm{1}+\mathrm{c}!\:\left(\mathrm{c}\neq\mathrm{2}\right)\:\mathrm{or}\:\mathrm{2}+\mathrm{c}!\:\left(\mathrm{c}\neq\mathrm{1}\right) \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{to}\:\mathrm{consider}\:\:\mathrm{cases}: \\ $$$$\left.\mathrm{I}\right)\mathrm{for}\:\mathrm{fixed}\:\mathrm{b}!=\mathrm{1}\Rightarrow\mathrm{b}=\mathrm{0}=\mathrm{1}\:\mathrm{c}\neq\mathrm{2} \\ $$$$\left.\mathrm{a}\right)\mathrm{assume}\:\mathrm{a}\leqslant\mathrm{c}\Rightarrow\mathrm{c}!\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{a}\right) \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{4}=\mathrm{1}+\mathrm{c}! \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{3}=\mathrm{c}!\:/:\mathrm{a} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{2a}+\mathrm{3}+^{} \frac{\mathrm{3}}{\mathrm{a}}=\frac{\mathrm{c}!}{\mathrm{a}} \\ $$$$\mathrm{LHS}\:\mathrm{is}\:\mathrm{integer}\:\mathrm{for}\:\mathrm{a}=\left\{\left(−\mathrm{1},\mathrm{1},\mathrm{2},\mathrm{3}\right)\right\} \\ $$$$\Rightarrow\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)=\left\{\left(−\mathrm{1},\mathrm{0},\mathrm{0}\right),\left(−\mathrm{1},\mathrm{1},\mathrm{0}\right),\left(−\mathrm{1},\mathrm{0},\mathrm{1}\right)\right. \\ $$$$\left.\left(−\mathrm{1},\mathrm{1},\mathrm{1}\right),\left(\mathrm{2},\mathrm{4},\mathrm{2}\right),\left(\mathrm{2},\mathrm{2},\mathrm{4}\right)\right\} \\ $$$$\left.\mathrm{b}\right)\mathrm{assume}\:\mathrm{c}<\mathrm{a} \\ $$$$\mathrm{c}!<\mathrm{a}! \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{3}<\mathrm{a}! \\ $$$$\mathrm{its}\:\mathrm{true}\:\mathrm{for}\:\mathrm{a}\geqslant\mathrm{6} \\ $$$$\mathrm{for}\:\mathrm{a}\geqslant\mathrm{6}\:\mathrm{let}\:\mathrm{a}=\mathrm{6}+\mathrm{k}\:\left(\mathrm{k}\geqslant\mathrm{0}\right) \\ $$$$\left(\mathrm{6}+\mathrm{k}\right)^{\mathrm{3}} +\mathrm{2}\left(\mathrm{6}+\mathrm{k}\right)^{\mathrm{2}} +\mathrm{3}\left(\mathrm{6}+\mathrm{k}\right)+\mathrm{3}=\mathrm{c}! \\ $$$$\mathrm{k}^{\mathrm{3}} +\mathrm{20k}^{\mathrm{2}} +\mathrm{35k}+\mathrm{309}=\mathrm{c}! \\ $$$$ \\ $$$$\:\mathrm{LHS}\:\mathrm{is}\:\mathrm{not}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2} \\ $$$$\mathrm{for}\:\mathrm{any}\:\mathrm{inter}\:\Rightarrow\:\mathrm{c}=\mathrm{0}\:\mathrm{or}\:\mathrm{c}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{k}=−\mathrm{7}\:\mathrm{is}\:\mathrm{no}\:\mathrm{solution}\:\left(\mathrm{k}\geqslant\mathrm{0}\right) \\ $$$$\left.\mathrm{c}\right)\mathrm{a}=\mathrm{0}\:\mathrm{no}\:\mathrm{solution} \\ $$$$\left.\mathrm{II}\right)\mathrm{For}\:\mathrm{fixed}\:\mathrm{b}!=\mathrm{2}\Rightarrow\mathrm{b}=\mathrm{2} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{2}=\mathrm{c}! \\ $$$$\left.\mathrm{a}\right)\mathrm{c}\geqslant\mathrm{a}\:\Rightarrow\mathrm{c}!\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{a}\right) \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{2}=\mathrm{c}!/:\mathrm{a} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{2a}+\mathrm{3a}+\frac{\mathrm{2}}{\mathrm{a}}=\frac{\mathrm{c}!}{\mathrm{a}} \\ $$$$\mathrm{LHS}\:\mathrm{is}\:\mathrm{integer}\:\mathrm{for}\:\mathrm{a}=\left\{\left(−\mathrm{1},\mathrm{1},\mathrm{2}\right)\right\}\:\mathrm{which}\:\mathrm{is} \\ $$$$\mathrm{already}\:\mathrm{checked}\:\mathrm{solutions} \\ $$$$\left.\mathrm{b}\right)\mathrm{c}<\mathrm{a} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{2a}^{\mathrm{2}} +\mathrm{3a}+\mathrm{2}<\mathrm{a}! \\ $$$$\mathrm{its}\:\mathrm{true}\:\mathrm{for}\:\mathrm{a}\geqslant\mathrm{6}\Rightarrow\mathrm{a}=\mathrm{6}+\mathrm{p}\:\mathrm{p}\geqslant\mathrm{0} \\ $$$$\mathrm{c}<\mathrm{6}+\mathrm{p} \\ $$$$\left(\mathrm{6}+\mathrm{p}\right)^{\mathrm{3}} +\mathrm{2}\left(\mathrm{6}+\mathrm{p}\right)^{\mathrm{2}} +\mathrm{3}\left(\mathrm{6}+\mathrm{p}\right)+\mathrm{2}=\mathrm{c}! \\ $$$$\mathrm{p}^{\mathrm{3}} +\mathrm{20p}^{\mathrm{2}} +\mathrm{135p}+\mathrm{308}=\mathrm{c}! \\ $$$$\mathrm{p}^{\mathrm{3}} +\mathrm{3p}^{\mathrm{2}} \centerdot\mathrm{7}+\mathrm{3p}\centerdot\mathrm{49}+\mathrm{343}−\left(\mathrm{p}^{\mathrm{2}} +\mathrm{12p}+\mathrm{35}\right)=\mathrm{c}! \\ $$$$\left(\mathrm{p}+\mathrm{7}\right)^{\mathrm{3}} −\left(\mathrm{p}+\mathrm{7}\right)\left(\mathrm{p}+\mathrm{5}\right)=\mathrm{c}! \\ $$$$\mathrm{p}+\mathrm{7}=\mathrm{t}\: \\ $$$$\mathrm{t}^{\mathrm{3}} −\mathrm{t}\left(\mathrm{t}−\mathrm{2}\right)=\mathrm{c}! \\ $$$$\mathrm{Since}\:\mathrm{c}<\mathrm{p}+\mathrm{6}\Rightarrow\mathrm{c}<\mathrm{t}−\mathrm{1}<\mathrm{t} \\ $$$$\mathrm{for}\:\mathrm{t}>\mathrm{1}\:\mathrm{c}≢\mathrm{0}\left(\mathrm{mod}\:\mathrm{t}\right)\Rightarrow\mathrm{c}!≢\mathrm{0}\left(\mathrm{mod}\:\mathrm{t}\right) \\ $$$$\mathrm{t}^{\mathrm{3}} −\mathrm{t}\left(\mathrm{t}−\mathrm{2}\right)\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{t}\right) \\ $$$$\mathrm{its}\:\mathrm{only}\:\mathrm{possible}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{t}=\mathrm{1} \\ $$$$\mathrm{c}!=\mathrm{1}^{\mathrm{3}} −\mathrm{1}^{\mathrm{2}} +\mathrm{2}\Rightarrow\mathrm{c}=\mathrm{2}\: \\ $$$$\mathrm{Its}\:\mathrm{contradiction}\:\mathrm{since}\:\mathrm{c}<\mathrm{t}−\mathrm{1} \\ $$$$\left.\mathrm{c}\right)\mathrm{a}=\mathrm{0}\Rightarrow\mathrm{c}=\mathrm{2} \\ $$$$\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)=\left\{\left(\mathrm{0},\mathrm{2},\mathrm{2}\right)\right\} \\ $$$$\underline{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}\:\:\:\: \\ $$$$\mathrm{All}\:\mathrm{solutions} \\ $$$$\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)=\left\{\left(−\mathrm{1},\mathrm{0},\mathrm{0}\right),\left(−\mathrm{1},\mathrm{0},\mathrm{1}\right),\left(−\mathrm{1},\mathrm{1},\mathrm{0}\right),\right. \\ $$$$\left.\left(−\mathrm{1},\mathrm{1},\mathrm{1}\right),\left(\mathrm{0},\mathrm{2},\mathrm{2}\right),\left(\mathrm{2},\mathrm{2},\mathrm{4}\right),\left(\mathrm{2},\mathrm{4},\mathrm{2}\right)\right\} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
	Commented by dragan91 last updated on 15/Jul/22

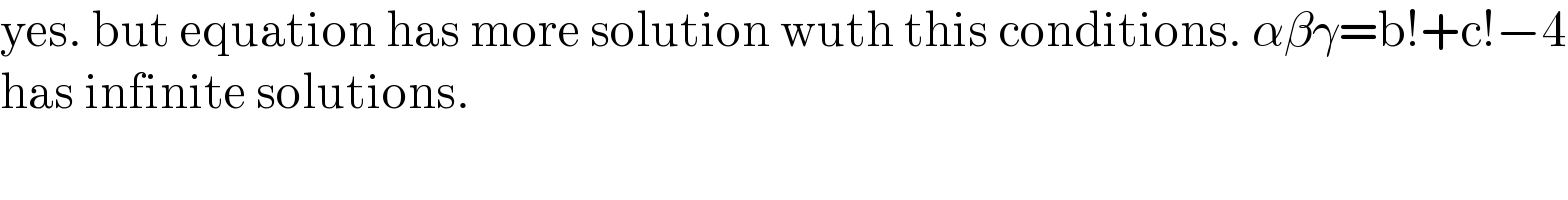
	$$\mathrm{yes}.\:\mathrm{but}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{more}\:\mathrm{solution}\:\mathrm{wuth}\:\mathrm{this}\:\mathrm{conditions}.\:\alpha\beta\gamma=\mathrm{b}!+\mathrm{c}!−\mathrm{4} \\ $$$$\mathrm{has}\:\mathrm{infinite}\:\mathrm{solutions}.\: \\ $$
	Commented by Rasheed.Sindhi last updated on 16/Jul/22

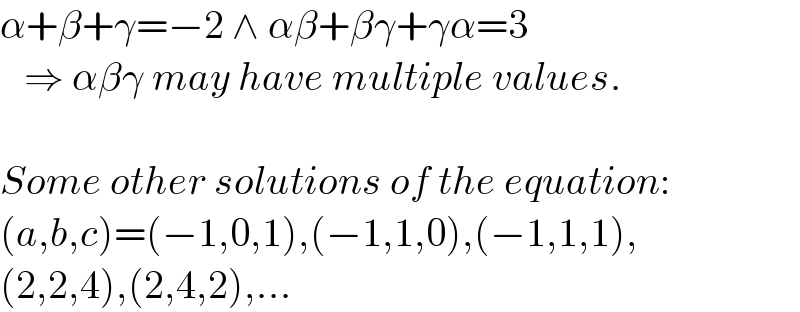
	$$\alpha+\beta+\gamma=−\mathrm{2}\:\wedge\:\alpha\beta+\beta\gamma+\gamma\alpha=\mathrm{3} \\ $$$$\:\:\:\Rightarrow\:\alpha\beta\gamma\:{may}\:{have}\:{multiple}\:{values}. \\ $$$$ \\ $$$${Some}\:{other}\:{solutions}\:{of}\:{the}\:{equation}: \\ $$$$\left({a},{b},{c}\right)=\left(−\mathrm{1},\mathrm{0},\mathrm{1}\right),\left(−\mathrm{1},\mathrm{1},\mathrm{0}\right),\left(−\mathrm{1},\mathrm{1},\mathrm{1}\right), \\ $$$$\left(\mathrm{2},\mathrm{2},\mathrm{4}\right),\left(\mathrm{2},\mathrm{4},\mathrm{2}\right),... \\ $$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum