
Question Number 175335 by infinityaction last updated on 27/Aug/22
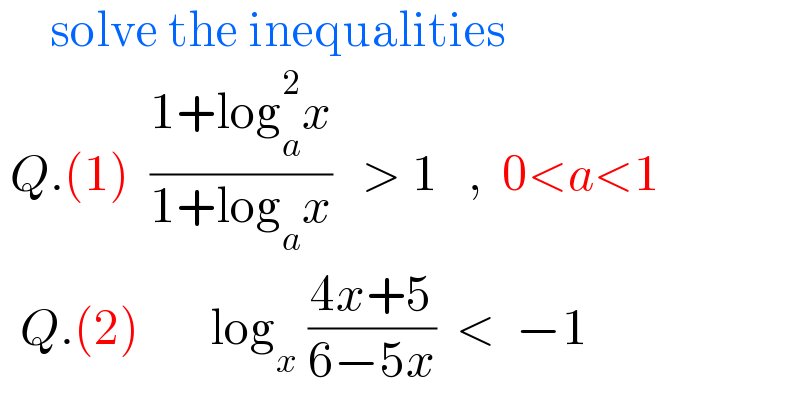
$$\:\:\:\:\:\mathrm{solve}\:\mathrm{the}\:\mathrm{inequalities} \\ $$ $$\:{Q}.\left(\mathrm{1}\right)\:\:\frac{\mathrm{1}+\mathrm{log}_{{a}} ^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{log}_{{a}} {x}}\:\:\:>\:\mathrm{1}\:\:\:,\:\:\mathrm{0}<{a}<\mathrm{1} \\ $$ $$\:\:{Q}.\left(\mathrm{2}\right)\:\:\:\:\:\:\:\mathrm{log}_{{x}} \:\frac{\mathrm{4}{x}+\mathrm{5}}{\mathrm{6}−\mathrm{5}{x}}\:\:<\:\:−\mathrm{1} \\ $$
Answered by blackmamba last updated on 27/Aug/22
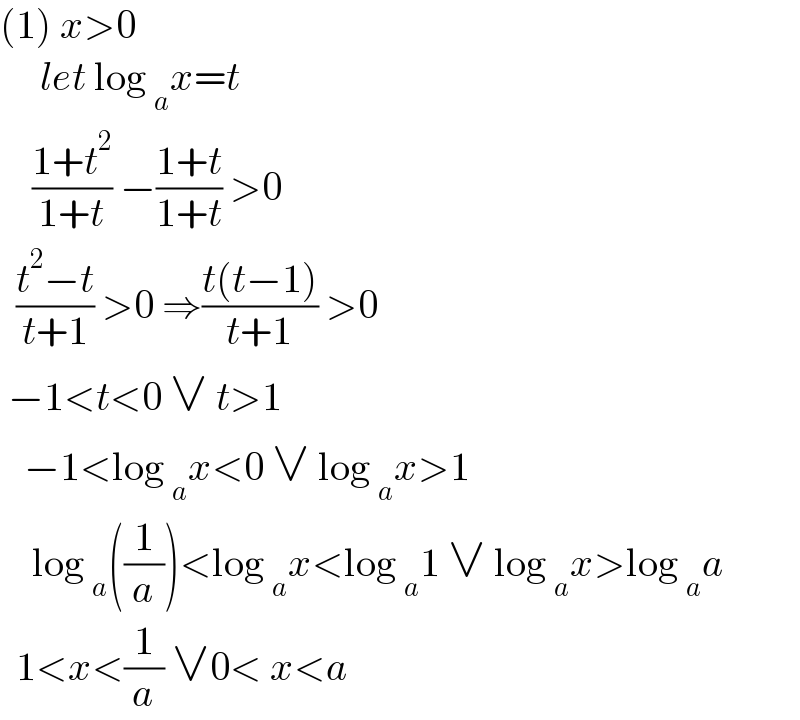
$$\left(\mathrm{1}\right)\:{x}>\mathrm{0} \\ $$ $$\:\:\:\:\:{let}\:\mathrm{log}\:_{{a}} {x}={t} \\ $$ $$\:\:\:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}}\:−\frac{\mathrm{1}+{t}}{\mathrm{1}+{t}}\:>\mathrm{0}\: \\ $$ $$\:\:\frac{{t}^{\mathrm{2}} −{t}}{{t}+\mathrm{1}}\:>\mathrm{0}\:\Rightarrow\frac{{t}\left({t}−\mathrm{1}\right)}{{t}+\mathrm{1}}\:>\mathrm{0} \\ $$ $$\:−\mathrm{1}<{t}<\mathrm{0}\:\vee\:{t}>\mathrm{1} \\ $$ $$\:\:\:−\mathrm{1}<\mathrm{log}\:_{{a}} {x}<\mathrm{0}\:\vee\:\mathrm{log}\:_{{a}} {x}>\mathrm{1} \\ $$ $$\:\:\:\:\mathrm{log}\:_{{a}} \left(\frac{\mathrm{1}}{{a}}\right)<\mathrm{log}\:_{{a}} {x}<\mathrm{log}\:_{{a}} \mathrm{1}\:\vee\:\mathrm{log}\:_{{a}} {x}>\mathrm{log}\:_{{a}} {a} \\ $$ $$\:\:\mathrm{1}<{x}<\frac{\mathrm{1}}{{a}}\:\vee\mathrm{0}<\:{x}<{a}\: \\ $$
Commented byinfinityaction last updated on 27/Aug/22

$${thanks} \\ $$
Answered by mahdipoor last updated on 27/Aug/22
![2: if a<b ⇒ { ((c^a <c^b if c≥1)),((c^a >c^b if 0<c<1)) :} ((4x+5)/(6−5x))>0⇒x∈(((−5)/4),(6/5)) (iii) ⇒⇒I: 0<x<1 (i) x^∧ (log_x ((4x+5)/(6−5x))) > x^∧ (−1) ⇒((4x+5)/(6−5x))>(1/x) ⇒ 4x^2 +10x−6>0 ⇒x∈R−[−3,(1/2)] (ii) i∩ii∩iii=0.5<x<1 ⇒⇒II: 1≤x (i) x^∧ (log_x ((4x+5)/(6−5x))) ≤ x^∧ (−1) ⇒((4x+5)/(6−5x))≤(1/x) ⇒ 4x^2 +10x−6≤0 ⇒x∈[−3,(1/2)] (ii) i∩ii∩iii=∄ I∩II= 0.5<x<1](Q175339.png)
$$\mathrm{2}:\:{if}\:{a}<{b}\:\Rightarrow\:\begin{cases}{{c}^{{a}} <{c}^{{b}} \:\:\:{if}\:\:{c}\geqslant\mathrm{1}}\\{{c}^{{a}} >{c}^{{b}} \:\:\:{if}\:\:\mathrm{0}<{c}<\mathrm{1}}\end{cases} \\ $$ $$\frac{\mathrm{4}{x}+\mathrm{5}}{\mathrm{6}−\mathrm{5}{x}}>\mathrm{0}\Rightarrow{x}\in\left(\frac{−\mathrm{5}}{\mathrm{4}},\frac{\mathrm{6}}{\mathrm{5}}\right)\:\:\left({iii}\right) \\ $$ $$\Rightarrow\Rightarrow\mathrm{I}:\:\:\:\mathrm{0}<{x}<\mathrm{1}\:\left({i}\right) \\ $$ $${x}^{\wedge} \left({log}_{{x}} \frac{\mathrm{4}{x}+\mathrm{5}}{\mathrm{6}−\mathrm{5}{x}}\right)\:>\:{x}^{\wedge} \left(−\mathrm{1}\right)\:\Rightarrow\frac{\mathrm{4}{x}+\mathrm{5}}{\mathrm{6}−\mathrm{5}{x}}>\frac{\mathrm{1}}{{x}}\:\Rightarrow\: \\ $$ $$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{6}>\mathrm{0}\:\Rightarrow{x}\in\mathrm{R}−\left[−\mathrm{3},\frac{\mathrm{1}}{\mathrm{2}}\right]\:\:\:\left({ii}\right) \\ $$ $${i}\cap{ii}\cap{iii}=\mathrm{0}.\mathrm{5}<{x}<\mathrm{1} \\ $$ $$\Rightarrow\Rightarrow\mathrm{II}:\:\:\mathrm{1}\leqslant{x}\:\:\:\left({i}\right) \\ $$ $${x}^{\wedge} \left({log}_{{x}} \frac{\mathrm{4}{x}+\mathrm{5}}{\mathrm{6}−\mathrm{5}{x}}\right)\:\leqslant\:{x}^{\wedge} \left(−\mathrm{1}\right)\:\Rightarrow\frac{\mathrm{4}{x}+\mathrm{5}}{\mathrm{6}−\mathrm{5}{x}}\leqslant\frac{\mathrm{1}}{{x}}\:\Rightarrow\: \\ $$ $$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{10}{x}−\mathrm{6}\leqslant\mathrm{0}\:\Rightarrow{x}\in\left[−\mathrm{3},\frac{\mathrm{1}}{\mathrm{2}}\right]\:\:\:\left({ii}\right) \\ $$ $${i}\cap{ii}\cap{iii}=\nexists \\ $$ $$\mathrm{I}\cap\mathrm{II}=\:\mathrm{0}.\mathrm{5}<{x}<\mathrm{1} \\ $$
Commented byinfinityaction last updated on 27/Aug/22

$${thanks} \\ $$
