Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 17625 by tawa tawa last updated on 08/Jul/17

Find the fourier series of : f(x) = x, from 0 < x < π

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{fourier}\:\mathrm{series}\:\mathrm{of}\::\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x},\:\:\mathrm{from}\:\:\:\mathrm{0}\:<\:\mathrm{x}\:<\:\pi \\ $$

Commented bytawa tawa last updated on 08/Jul/17

please help with this.

$$\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{this}. \\ $$

Answered by alex041103 last updated on 09/Jul/17

(π/2)−Σ_(n=1) ^∞ ((sin(2nx))/n) = f(x) = x when x∈(0, π)

$$\frac{\pi}{\mathrm{2}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left(\mathrm{2}{nx}\right)}{{n}}\:=\:{f}\left({x}\right)\:=\:{x}\:{when}\:{x}\in\left(\mathrm{0},\:\pi\right) \\ $$

Commented bytawa tawa last updated on 09/Jul/17

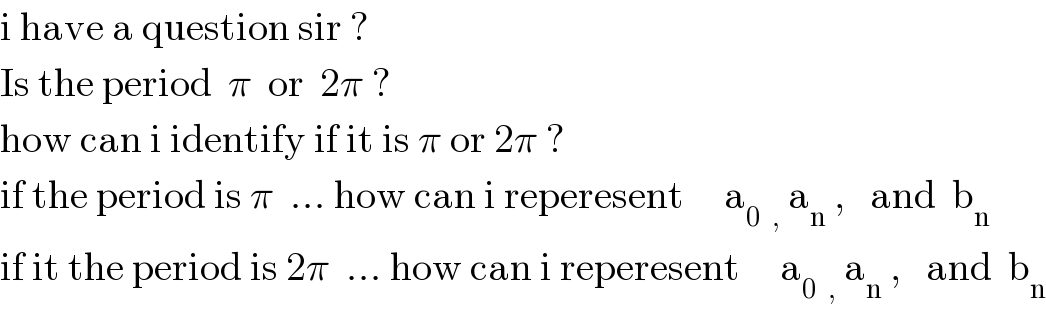
i have a question sir ? Is the period π or 2π ? how can i identify if it is π or 2π ? if the period is π ... how can i reperesent a_(0 , ) a_n , and b_n if it the period is 2π ... how can i reperesent a_(0 , ) a_n , and b_n

$$\mathrm{i}\:\mathrm{have}\:\mathrm{a}\:\mathrm{question}\:\mathrm{sir}\:? \\ $$ $$\mathrm{Is}\:\mathrm{the}\:\mathrm{period}\:\:\pi\:\:\mathrm{or}\:\:\mathrm{2}\pi\:? \\ $$ $$\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{identify}\:\mathrm{if}\:\mathrm{it}\:\mathrm{is}\:\pi\:\mathrm{or}\:\mathrm{2}\pi\:? \\ $$ $$\mathrm{if}\:\mathrm{the}\:\mathrm{period}\:\mathrm{is}\:\pi\:\:...\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{reperesent}\:\:\:\:\:\mathrm{a}_{\mathrm{0}\:\:\:,\:\:} \mathrm{a}_{\mathrm{n}} \:,\:\:\:\mathrm{and}\:\:\mathrm{b}_{\mathrm{n}} \\ $$ $$\mathrm{if}\:\mathrm{it}\:\mathrm{the}\:\mathrm{period}\:\mathrm{is}\:\mathrm{2}\pi\:\:...\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{reperesent}\:\:\:\:\:\mathrm{a}_{\mathrm{0}\:\:\:,\:\:} \mathrm{a}_{\mathrm{n}} \:,\:\:\:\mathrm{and}\:\:\mathrm{b}_{\mathrm{n}} \\ $$

Commented byalex041103 last updated on 09/Jul/17

It′s easy to prove that if f(x)=c+Σ_(n=1) ^∞ [a_n cos(((2πnx)/T)) + b_n sin(((2πnx)/T))] then c=(1/T)∫_0 ^T f(x) dx a_n =(2/T)∫_0 ^T f(x)cos(((2πnx)/T)) dx b_b =(2/T)∫_0 ^T f(x)sin(((2πnx)/T)) dx In the case of f(x)=x we will set the period T=π ⇒c=(π/2) , a_n =0 , b_n =−(1/n) ⇒x∈(0, π), f(x)=(π/2) − Σ_(n=1) ^∞ ((sin(2nx))/n)

$$ \\ $$ $${It}'{s}\:{easy}\:{to}\:{prove}\:{that}\:{if} \\ $$ $${f}\left({x}\right)={c}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[{a}_{{n}} {cos}\left(\frac{\mathrm{2}\pi{nx}}{{T}}\right)\:+\:{b}_{{n}} {sin}\left(\frac{\mathrm{2}\pi{nx}}{{T}}\right)\right] \\ $$ $${then} \\ $$ $${c}=\frac{\mathrm{1}}{{T}}\underset{\mathrm{0}} {\overset{{T}} {\int}}{f}\left({x}\right)\:{dx} \\ $$ $${a}_{{n}} =\frac{\mathrm{2}}{{T}}\underset{\mathrm{0}} {\overset{{T}} {\int}}{f}\left({x}\right){cos}\left(\frac{\mathrm{2}\pi{nx}}{{T}}\right)\:{dx} \\ $$ $${b}_{{b}} =\frac{\mathrm{2}}{{T}}\underset{\mathrm{0}} {\overset{{T}} {\int}}{f}\left({x}\right){sin}\left(\frac{\mathrm{2}\pi{nx}}{{T}}\right)\:{dx} \\ $$ $$ \\ $$ $${In}\:{the}\:{case}\:{of}\:{f}\left({x}\right)={x}\:{we}\:{will}\:{set}\:{the}\:{period}\: \\ $$ $${T}=\pi \\ $$ $$\Rightarrow{c}=\frac{\pi}{\mathrm{2}}\:,\:{a}_{{n}} =\mathrm{0}\:,\:{b}_{{n}} =−\frac{\mathrm{1}}{{n}} \\ $$ $$\Rightarrow{x}\in\left(\mathrm{0},\:\pi\right),\:{f}\left({x}\right)=\frac{\pi}{\mathrm{2}}\:−\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$

Commented bytawa tawa last updated on 09/Jul/17

That means for period 2π a_0 = (1/π) ∫_( 0) ^( 2π) f(x) a_n = (1/π) ∫_( 0) ^( 2π) f(x)cos(nx) b_n = (1/π) ∫_( 0) ^( 2π) f(x)sin(nx) Again, That means for period π a_0 = (2/π) ∫_( 0) ^( π) f(x) a_n = (2/π) ∫_( 0) ^( π) f(x)cos(nx) b_n = (2/π) ∫_( 0) ^( π) f(x)sin(nx) ??????????????

$$\mathrm{That}\:\mathrm{means}\:\mathrm{for}\:\mathrm{period}\:\:\mathrm{2}\pi \\ $$ $$\mathrm{a}_{\mathrm{0}} \:=\:\frac{\mathrm{1}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}\pi} \mathrm{f}\left(\mathrm{x}\right) \\ $$ $$\mathrm{a}_{\mathrm{n}} \:=\:\frac{\mathrm{1}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right) \\ $$ $$\mathrm{b}_{\mathrm{n}} \:=\:\frac{\mathrm{1}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{sin}\left(\mathrm{nx}\right) \\ $$ $$\mathrm{Again}, \\ $$ $$\mathrm{That}\:\mathrm{means}\:\mathrm{for}\:\mathrm{period}\:\:\pi \\ $$ $$\mathrm{a}_{\mathrm{0}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right) \\ $$ $$\mathrm{a}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right) \\ $$ $$\mathrm{b}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{sin}\left(\mathrm{nx}\right) \\ $$ $$?????????????? \\ $$

Commented byalex041103 last updated on 09/Jul/17

No. For period of π we have: b_n = (2/π) ∫_( 0) ^( π) f(x)sin(((2π)/π)nx)dx=(2/π)∫_0 ^π f(x)sin(2nx) dx a_n = (2/π) ∫_( 0) ^( π) f(x)cos(((2π)/π)nx) dx=(2/π)∫_0 ^π f(x)cos(2nx) dx a_0 = (2/π) ∫_( 0) ^( π) f(x) dx And in fact if we use T=2π(the period is 2π) we are going to get fourier seriesfor f(x)=x for x∈[0, 2π]

$${No}. \\ $$ $${For}\:{period}\:{of}\:\pi\:{we}\:{have}: \\ $$ $$\mathrm{b}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\pi}\mathrm{nx}\right){dx}=\frac{\mathrm{2}}{\pi}\underset{\mathrm{0}} {\overset{\pi} {\int}}{f}\left({x}\right){sin}\left(\mathrm{2}{nx}\right)\:{dx} \\ $$ $$\mathrm{a}_{\mathrm{n}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\pi}\mathrm{nx}\right)\:{dx}=\frac{\mathrm{2}}{\pi}\underset{\mathrm{0}} {\overset{\pi} {\int}}{f}\left({x}\right){cos}\left(\mathrm{2}{nx}\right)\:{dx} \\ $$ $$\mathrm{a}_{\mathrm{0}} \:=\:\frac{\mathrm{2}}{\pi}\:\int_{\:\mathrm{0}} ^{\:\pi} \mathrm{f}\left(\mathrm{x}\right)\:{dx} \\ $$ $${And}\:{in}\:{fact}\:{if}\:{we}\:{use}\:{T}=\mathrm{2}\pi\left({the}\:{period}\:{is}\:\mathrm{2}\pi\right)\: \\ $$ $${we}\:{are}\:{going}\:{to}\:{get}\:{fourier}\:{seriesfor} \\ $$ $${f}\left({x}\right)={x}\:{for}\:{x}\in\left[\mathrm{0},\:\mathrm{2}\pi\right] \\ $$

Commented bytawa tawa last updated on 09/Jul/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented byalex041103 last updated on 10/Jul/17

Commented byalex041103 last updated on 10/Jul/17

Blue→T=2π,i.e. for 0<x<2π x=π−2Σ_(n=1) ^∞ ((sin(nx))/n) Red→T=π,i.e. for 0<x<π x=(π/2)−Σ_(n=1) ^∞ ((sin(2nx))/n)

$$\mathrm{Blue}\rightarrow\mathrm{T}=\mathrm{2}\pi,\mathrm{i}.\mathrm{e}.\:\mathrm{for}\:\mathrm{0}<\mathrm{x}<\mathrm{2}\pi \\ $$ $$\mathrm{x}=\pi−\mathrm{2}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{nx}\right)}{\mathrm{n}} \\ $$ $$\mathrm{Red}\rightarrow\mathrm{T}=\pi,\mathrm{i}.\mathrm{e}.\:\mathrm{for}\:\mathrm{0}<\mathrm{x}<\pi \\ $$ $$\mathrm{x}=\frac{\pi}{\mathrm{2}}−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2nx}\right)}{\mathrm{n}} \\ $$

Commented bytawa tawa last updated on 10/Jul/17

i really appreciate your effort sir. God bless you.

$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com