
Question Number 177628 by mr W last updated on 07/Oct/22

Commented by mr W last updated on 07/Oct/22
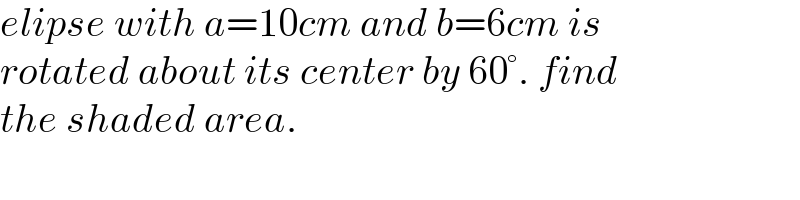
$${elipse}\:{with}\:{a}=\mathrm{10}{cm}\:{and}\:{b}=\mathrm{6}{cm}\:{is} \\ $$$${rotated}\:{about}\:{its}\:{center}\:{by}\:\mathrm{60}°.\:{find} \\ $$$${the}\:{shaded}\:{area}. \\ $$
Answered by mr W last updated on 08/Oct/22

Commented by mr W last updated on 09/Oct/22
![red elipse: (x^2 /(10^2 ))+(y^2 /6^2 )=1 ((r^2 cos^2 θ)/(10^2 ))+((y^2 sin^2 θ)/6^2 )=1 ⇒r=((60)/( (√(36 cos^2 θ+100 sin^2 θ)))) blue elipse: ⇒r=((60)/( (√(36 cos^2 (θ−ϕ)+100 sin^2 (θ−ϕ))))) intersection point P, Q: ((60)/( (√(36 cos^2 (θ−ϕ)+100 sin^2 (θ−ϕ)))))=((60)/( (√(36 cos^2 θ+100 sin^2 θ)))) 36 cos^2 (θ−ϕ)+100 sin^2 (θ−ϕ)=36 cos^2 θ+100 sin^2 θ 9 [cos^2 (θ−ϕ)−cos^2 θ]+25 [sin^2 (θ−ϕ)−sin^2 θ]=0 9 [cos (θ−ϕ)+cos θ][cos (θ−ϕ)−cos θ]+25 [sin (θ−ϕ)+sin θ][sin (θ−ϕ)−sin θ]=0 9(cos θ cos ϕ+sin θ sin ϕ+cos θ)(cos θ cos ϕ+sin θ sin ϕ−cos θ)+25 (sin θ cos ϕ−cos θ sin ϕ+sin θ)(sin θ cos ϕ−cos θ sin ϕ−sin θ)=0 9(((1+cos ϕ)/(sin ϕ))+tan θ)(((1−cos ϕ)/(sin ϕ))−tan θ)+25(((1+cos ϕ)/(sin ϕ))tan θ−1)(((1−cos ϕ)/(sin ϕ))tan θ+1)=0 tan^2 θ+((2 tan θ)/(tan ϕ))−1=0 with ϕ=60° tan^2 θ+((2 tan θ)/( (√3)))−1=0 tan θ=((−1±2)/( (√3)))= { ((1/( (√3)))),((−(√3))) :} ⇒θ_Q =(π/6) ⇒θ_P =π−(π/3)=((2π)/3) area of sector of blue elipse: A_(blue sector) =(1/2)∫_(θ_Q −ϕ) ^(θ_P −ϕ) r^2 dθ area of sector of red elipse: A_(red sector) =(1/2)∫_θ_Q ^θ_P r^2 dθ shaded are=2(sector blue−sector red): A_(shaded) =∫_(θ_Q −ϕ) ^(θ_P −ϕ) r^2 dθ−∫_θ_Q ^θ_P r^2 dθ A_(shaded) =∫_(θ_Q −ϕ) ^θ_Q r^2 dθ−∫_(θ_P −ϕ) ^θ_P r^2 dθ ∫(dθ/(b^2 cos^2 θ+a^2 sin^2 θ))=(1/(ab))×tan^(−1) ((a/b)×tan θ)+C ∫r^2 dθ=∫((3600 dθ)/( 36 cos^2 θ+100 sin^2 θ)) =60 tan^(−1) (((5 tan θ)/3))+C (A_(shadex) /(60))=[tan^(−1) (((5 tan θ)/3))]_(θ_Q −(π/3)) ^θ_Q −[tan^(−1) (((5 tan θ)/3))]_(θ_P −(π/3)) ^θ_P (A_(shadex) /(60))=[tan^(−1) (((5 tan θ)/3))]_(−(π/6)) ^(π/6) −[tan^(−1) (((5 tan θ)/3))]_(π/3) ^((2π)/3) (A_(shadex) /(60))=2 tan^(−1) ((5/( 3(√3))))−[π−2 tan^(−1) ((5/( (√3))))] (A_(shadex) /(60))=2[tan^(−1) ((5/(3(√3))))+tan^(−1) ((5/( (√3))))]−π A_(shaded) =120[tan^(−1) ((5/(3(√3))))+tan^(−1) ((5/( (√3))))]−60π ≈51.9227](Q177697.png)
$${red}\:{elipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{10}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{6}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{10}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{6}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{r}=\frac{\mathrm{60}}{\:\sqrt{\mathrm{36}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{100}\:\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$${blue}\:{elipse}: \\ $$$$\Rightarrow{r}=\frac{\mathrm{60}}{\:\sqrt{\mathrm{36}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\varphi\right)+\mathrm{100}\:\mathrm{sin}^{\mathrm{2}} \:\left(\theta−\varphi\right)}} \\ $$$${intersection}\:{point}\:{P},\:{Q}: \\ $$$$\frac{\mathrm{60}}{\:\sqrt{\mathrm{36}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\varphi\right)+\mathrm{100}\:\mathrm{sin}^{\mathrm{2}} \:\left(\theta−\varphi\right)}}=\frac{\mathrm{60}}{\:\sqrt{\mathrm{36}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{100}\:\mathrm{sin}^{\mathrm{2}} \:\theta}} \\ $$$$\mathrm{36}\:\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\varphi\right)+\mathrm{100}\:\mathrm{sin}^{\mathrm{2}} \:\left(\theta−\varphi\right)=\mathrm{36}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{100}\:\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\mathrm{9}\:\left[\mathrm{cos}^{\mathrm{2}} \:\left(\theta−\varphi\right)−\mathrm{cos}^{\mathrm{2}} \:\theta\right]+\mathrm{25}\:\left[\mathrm{sin}^{\mathrm{2}} \:\left(\theta−\varphi\right)−\mathrm{sin}^{\mathrm{2}} \:\theta\right]=\mathrm{0} \\ $$$$\mathrm{9}\:\left[\mathrm{cos}\:\left(\theta−\varphi\right)+\mathrm{cos}\:\theta\right]\left[\mathrm{cos}\:\left(\theta−\varphi\right)−\mathrm{cos}\:\theta\right]+\mathrm{25}\:\left[\mathrm{sin}\:\left(\theta−\varphi\right)+\mathrm{sin}\:\theta\right]\left[\mathrm{sin}\:\left(\theta−\varphi\right)−\mathrm{sin}\:\theta\right]=\mathrm{0} \\ $$$$\mathrm{9}\left(\mathrm{cos}\:\theta\:\mathrm{cos}\:\varphi+\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi+\mathrm{cos}\:\theta\right)\left(\mathrm{cos}\:\theta\:\mathrm{cos}\:\varphi+\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi−\mathrm{cos}\:\theta\right)+\mathrm{25}\:\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\varphi−\mathrm{cos}\:\theta\:\mathrm{sin}\:\varphi+\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\varphi−\mathrm{cos}\:\theta\:\mathrm{sin}\:\varphi−\mathrm{sin}\:\theta\right)=\mathrm{0} \\ $$$$\mathrm{9}\left(\frac{\mathrm{1}+\mathrm{cos}\:\varphi}{\mathrm{sin}\:\varphi}+\mathrm{tan}\:\theta\right)\left(\frac{\mathrm{1}−\mathrm{cos}\:\varphi}{\mathrm{sin}\:\varphi}−\mathrm{tan}\:\theta\right)+\mathrm{25}\left(\frac{\mathrm{1}+\mathrm{cos}\:\varphi}{\mathrm{sin}\:\varphi}\mathrm{tan}\:\theta−\mathrm{1}\right)\left(\frac{\mathrm{1}−\mathrm{cos}\:\varphi}{\mathrm{sin}\:\varphi}\mathrm{tan}\:\theta+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta+\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{tan}\:\varphi}−\mathrm{1}=\mathrm{0} \\ $$$${with}\:\varphi=\mathrm{60}° \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta+\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{3}}}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta=\frac{−\mathrm{1}\pm\mathrm{2}}{\:\sqrt{\mathrm{3}}}=\begin{cases}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\\{−\sqrt{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow\theta_{{Q}} =\frac{\pi}{\mathrm{6}} \\ $$$$\Rightarrow\theta_{{P}} =\pi−\frac{\pi}{\mathrm{3}}=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$ \\ $$$${area}\:{of}\:{sector}\:{of}\:{blue}\:{elipse}: \\ $$$${A}_{{blue}\:{sector}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\theta_{{Q}} −\varphi} ^{\theta_{{P}} −\varphi} {r}^{\mathrm{2}} {d}\theta \\ $$$${area}\:{of}\:{sector}\:{of}\:{red}\:{elipse}: \\ $$$${A}_{{red}\:{sector}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\theta_{{Q}} } ^{\theta_{{P}} } {r}^{\mathrm{2}} {d}\theta \\ $$$${shaded}\:{are}=\mathrm{2}\left({sector}\:{blue}−{sector}\:{red}\right): \\ $$$${A}_{{shaded}} =\int_{\theta_{{Q}} −\varphi} ^{\theta_{{P}} −\varphi} {r}^{\mathrm{2}} {d}\theta−\int_{\theta_{{Q}} } ^{\theta_{{P}} } {r}^{\mathrm{2}} {d}\theta \\ $$$${A}_{{shaded}} =\int_{\theta_{{Q}} −\varphi} ^{\theta_{{Q}} } {r}^{\mathrm{2}} {d}\theta−\int_{\theta_{{P}} −\varphi} ^{\theta_{{P}} } {r}^{\mathrm{2}} {d}\theta \\ $$$$\int\frac{{d}\theta}{{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}=\frac{\mathrm{1}}{{ab}}×\mathrm{tan}^{−\mathrm{1}} \left(\frac{{a}}{{b}}×\mathrm{tan}\:\theta\right)+{C} \\ $$$$\int{r}^{\mathrm{2}} {d}\theta=\int\frac{\mathrm{3600}\:{d}\theta}{\:\mathrm{36}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{100}\:\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{60}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}\:\mathrm{tan}\:\theta}{\mathrm{3}}\right)+{C} \\ $$$$\frac{{A}_{{shadex}} }{\mathrm{60}}=\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}\:\mathrm{tan}\:\theta}{\mathrm{3}}\right)\right]_{\theta_{{Q}} −\frac{\pi}{\mathrm{3}}} ^{\theta_{{Q}} } −\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}\:\mathrm{tan}\:\theta}{\mathrm{3}}\right)\right]_{\theta_{{P}} −\frac{\pi}{\mathrm{3}}} ^{\theta_{{P}} } \\ $$$$\frac{{A}_{{shadex}} }{\mathrm{60}}=\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}\:\mathrm{tan}\:\theta}{\mathrm{3}}\right)\right]_{−\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{6}}} −\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}\:\mathrm{tan}\:\theta}{\mathrm{3}}\right)\right]_{\frac{\pi}{\mathrm{3}}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\frac{{A}_{{shadex}} }{\mathrm{60}}=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\:\mathrm{3}\sqrt{\mathrm{3}}}\right)−\left[\pi−\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\:\sqrt{\mathrm{3}}}\right)\right] \\ $$$$\frac{{A}_{{shadex}} }{\mathrm{60}}=\mathrm{2}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\:\sqrt{\mathrm{3}}}\right)\right]−\pi \\ $$$${A}_{{shaded}} =\mathrm{120}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\:\sqrt{\mathrm{3}}}\right)\right]−\mathrm{60}\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{51}.\mathrm{9227} \\ $$
Commented by a.lgnaoui last updated on 08/Oct/22
$${Bonne}\:{interpretation}\:{Merci}. \\ $$
Commented by mr W last updated on 09/Oct/22

Commented by mr W last updated on 09/Oct/22
![alternative: A_(shaded) =A_(elipse) −4A_(red sector) =60π−2×60[tan^(−1) (((5 tan θ)/3))]_(π/6) ^((2π)/3) =60π−2×60[π−tan^(−1) (((5(√3))/3))−tan^(−1) ((5/(3(√3))))] =120[tan^(−1) (((5(√3))/3))+tan^(−1) ((5/(3(√3))))]−60π ≈51.9227](Q177783.png)
$${alternative}: \\ $$$${A}_{{shaded}} ={A}_{{elipse}} −\mathrm{4}{A}_{{red}\:{sector}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{60}\pi−\mathrm{2}×\mathrm{60}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}\:\mathrm{tan}\:\theta}{\mathrm{3}}\right)\right]_{\frac{\pi}{\mathrm{6}}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{60}\pi−\mathrm{2}×\mathrm{60}\left[\pi−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{120}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{3}}}\right)\right]−\mathrm{60}\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{51}.\mathrm{9227} \\ $$
Commented by Tawa11 last updated on 09/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
