
Question Number 179862 by cherokeesay last updated on 03/Nov/22
Commented by CElcedricjunior last updated on 03/Nov/22
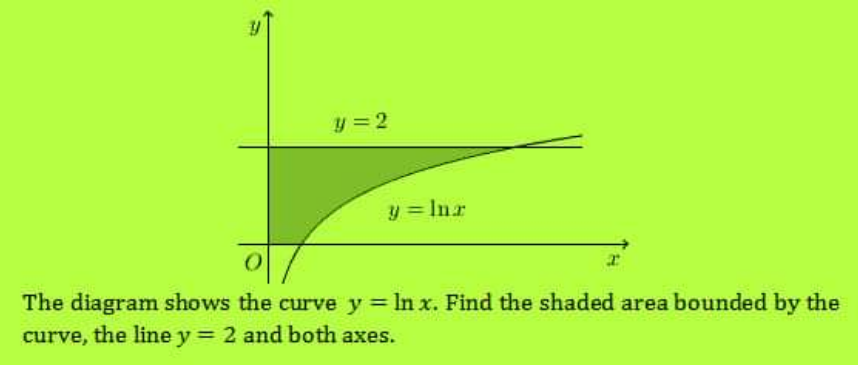
![{ ((y=lnx)),((y=2)) :}=>lnx=2=>x=e^2 =>x∈]0;e^2 ] et y∈[lnx;2] ⇔A=∫_(lnx) ^2 ∫_0 ^e^2 dxdy ⇔A=_ ∫_0 ^e^2 [2−lnx]dx ⇔A=[3x−xlnx]_0 ^e^2 A=3e^2 −2e^2 =e^2 A=e^2 um ...................le celebre cedric junior.......](Q179884.png)
$$\begin{cases}{\boldsymbol{{y}}=\boldsymbol{{lnx}}}\\{\boldsymbol{{y}}=\mathrm{2}}\end{cases}=>\boldsymbol{{lnx}}=\mathrm{2}=>\boldsymbol{{x}}=\boldsymbol{{e}}^{\mathrm{2}} \\ $$$$\left.=\left.>\boldsymbol{{x}}\in\right]\mathrm{0};\boldsymbol{{e}}^{\mathrm{2}} \right]\:\boldsymbol{{et}}\:\boldsymbol{{y}}\in\left[\boldsymbol{{lnx}};\mathrm{2}\right] \\ $$$$\Leftrightarrow\boldsymbol{{A}}=\int_{\boldsymbol{{lnx}}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\boldsymbol{{e}}^{\mathrm{2}} } \boldsymbol{{dxdy}} \\ $$$$\Leftrightarrow\boldsymbol{{A}}=_{} \int_{\mathrm{0}} ^{\boldsymbol{{e}}^{\mathrm{2}} } \left[\mathrm{2}−\boldsymbol{{lnx}}\right]\boldsymbol{{dx}} \\ $$$$\Leftrightarrow\boldsymbol{{A}}=\left[\mathrm{3}\boldsymbol{{x}}−\boldsymbol{{xlnx}}\right]_{\mathrm{0}} ^{\boldsymbol{{e}}^{\mathrm{2}} } \\ $$$$\boldsymbol{{A}}=\mathrm{3}\boldsymbol{{e}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{e}}^{\mathrm{2}} =\boldsymbol{{e}}^{\mathrm{2}} \\ $$$$\boldsymbol{{A}}={e}^{\mathrm{2}} \:\:{um} \\ $$$$...................{le}\:{celebre}\:{cedric}\:{junior}....... \\ $$$$ \\ $$
Commented by JDamian last updated on 03/Nov/22
that's clearly wrong
Answered by som(math1967) last updated on 03/Nov/22
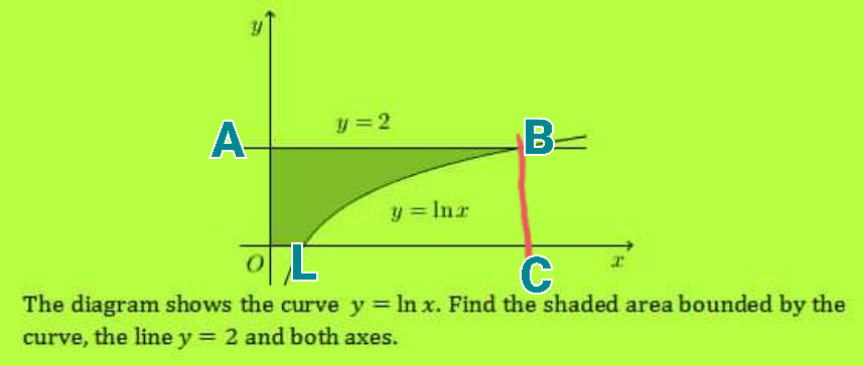
![co ordinate L⇒lnx=0⇒x=1 L(1,0) B⇒(e^2 ,2) shaded area =e^2 ×2−∫_1 ^e^2 lnxdx =2e^2 −[xlnx−x]_1 ^e^2 =2e^2 −[e^2 lne^2 −e^2 −0+1] =2e^2 −[e^2 +1] =(e^2 −1)squnit e=2.71..](Q179864.png)
$$\:{co}\:{ordinate}\:{L}\Rightarrow{lnx}=\mathrm{0}\Rightarrow{x}=\mathrm{1} \\ $$$$\:{L}\left(\mathrm{1},\mathrm{0}\right)\:{B}\Rightarrow\left({e}^{\mathrm{2}} ,\mathrm{2}\right) \\ $$$${shaded}\:{area} \\ $$$$={e}^{\mathrm{2}} ×\mathrm{2}−\int_{\mathrm{1}} ^{{e}^{\mathrm{2}} } {lnxdx} \\ $$$$=\mathrm{2}{e}^{\mathrm{2}} −\left[{xlnx}−{x}\right]_{\mathrm{1}} ^{{e}^{\mathrm{2}} } \\ $$$$=\mathrm{2}{e}^{\mathrm{2}} −\left[{e}^{\mathrm{2}} {lne}^{\mathrm{2}} −{e}^{\mathrm{2}} −\mathrm{0}+\mathrm{1}\right] \\ $$$$=\mathrm{2}{e}^{\mathrm{2}} −\left[{e}^{\mathrm{2}} +\mathrm{1}\right] \\ $$$$=\left({e}^{\mathrm{2}} −\mathrm{1}\right){squnit} \\ $$$${e}=\mathrm{2}.\mathrm{71}.. \\ $$
Commented by som(math1967) last updated on 03/Nov/22
Commented by som(math1967) last updated on 03/Nov/22
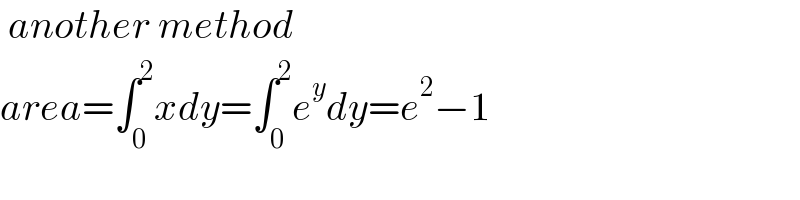
$$\:{another}\:{method} \\ $$$${area}=\int_{\mathrm{0}} ^{\mathrm{2}} {xdy}=\int_{\mathrm{0}} ^{\mathrm{2}} {e}^{{y}} {dy}={e}^{\mathrm{2}} −\mathrm{1} \\ $$
Commented by Acem last updated on 03/Nov/22

$${Yessss}!\:{Thanks} \\ $$
Answered by Acem last updated on 03/Nov/22
![the two limits x= 1 → e^2 Area= 2+ 2(e^2 −1)−∫_1 ^( e^2 ) ln x dx = 2e^2 − [x ln x−x] ∣_( 1) ^e^2 = 2e^2 −(2e^2 −e^2 +1) Area= e^2 −1= 6.389 un.^2](Q179866.png)
$$\:{the}\:{two}\:{limits}\:{x}=\:\mathrm{1}\:\rightarrow\:{e}^{\mathrm{2}} \\ $$$$\:{Area}=\:\mathrm{2}+\:\mathrm{2}\left({e}^{\mathrm{2}} −\mathrm{1}\right)−\int_{\mathrm{1}} ^{\:{e}^{\mathrm{2}} } \:\mathrm{ln}\:{x}\:{dx} \\ $$$$\:=\:\mathrm{2}{e}^{\mathrm{2}} −\:\left[{x}\:\mathrm{ln}\:{x}−{x}\right]\:\mid_{\:\mathrm{1}} ^{{e}^{\mathrm{2}} } =\:\mathrm{2}{e}^{\mathrm{2}} −\left(\mathrm{2}{e}^{\mathrm{2}} −{e}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:{Area}=\:{e}^{\mathrm{2}} −\mathrm{1}=\:\mathrm{6}.\mathrm{389}\:{un}.^{\mathrm{2}} \\ $$
