Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 182852 by mnjuly1970 last updated on 16/Dec/22

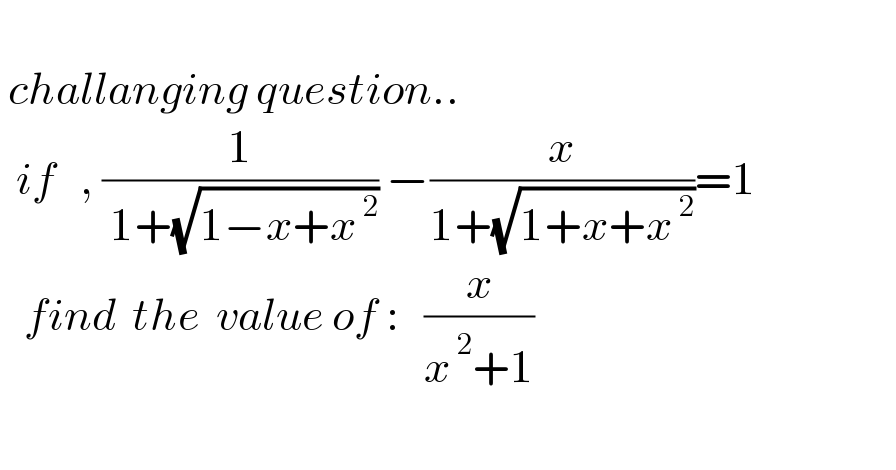
challanging question.. if , (1/( 1+(√(1−x+x^( 2) )))) −(x/(1+(√(1+x+x^( 2) ))))=1 find the value of : (x/(x^( 2) +1))

$$ \\ $$$$\:{challanging}\:{question}.. \\ $$$$\:\:{if}\:\:\:,\:\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{\mathrm{1}−{x}+{x}^{\:\mathrm{2}} }}\:−\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{1}+{x}+{x}^{\:\mathrm{2}} }}=\mathrm{1} \\ $$$$\:\:\:{find}\:\:{the}\:\:{value}\:{of}\::\:\:\:\frac{{x}}{{x}^{\:\mathrm{2}} +\mathrm{1}} \\ $$$$ \\ $$

Commented by Frix last updated on 15/Dec/22

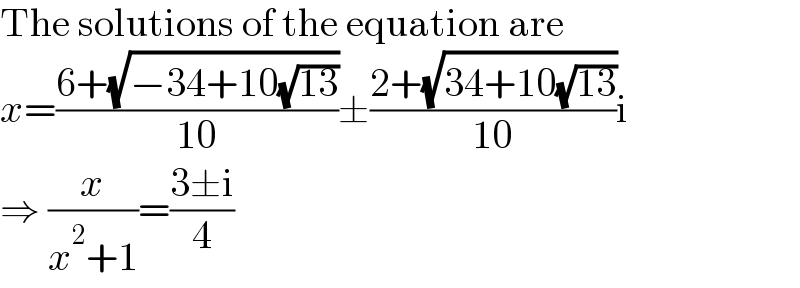
The solutions of the equation are x=((6+(√(−34+10(√(13)))))/(10))±((2+(√(34+10(√(13)))))/(10))i ⇒ (x/(x^2 +1))=((3±i)/4)

$$\mathrm{The}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{are} \\ $$$${x}=\frac{\mathrm{6}+\sqrt{−\mathrm{34}+\mathrm{10}\sqrt{\mathrm{13}}}}{\mathrm{10}}\pm\frac{\mathrm{2}+\sqrt{\mathrm{34}+\mathrm{10}\sqrt{\mathrm{13}}}}{\mathrm{10}}\mathrm{i} \\ $$$$\Rightarrow\:\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{3}\pm\mathrm{i}}{\mathrm{4}} \\ $$

Commented by Frix last updated on 16/Dec/22

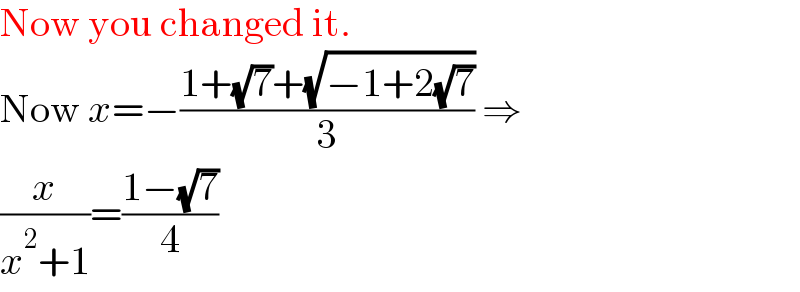
Now you changed it. Now x=−((1+(√7)+(√(−1+2(√7))))/3) ⇒ (x/(x^2 +1))=((1−(√7))/4)

$$\mathrm{Now}\:\mathrm{you}\:\mathrm{changed}\:\mathrm{it}. \\ $$$$\mathrm{Now}\:{x}=−\frac{\mathrm{1}+\sqrt{\mathrm{7}}+\sqrt{−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{7}}}}{\mathrm{3}}\:\Rightarrow \\ $$$$\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}−\sqrt{\mathrm{7}}}{\mathrm{4}} \\ $$

Answered by Rasheed.Sindhi last updated on 16/Dec/22

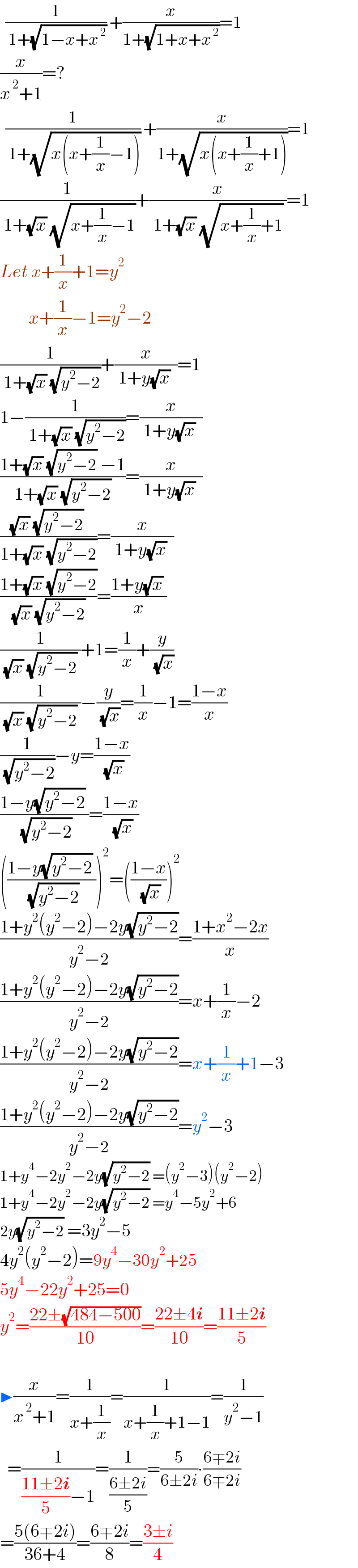
(1/( 1+(√(1−x+x^( 2) )))) +(x/(1+(√(1+x+x^( 2) ))))=1 (x/(x^( 2) +1))=? (1/( 1+(√(x(x+(1/x)−1))))) +(x/(1+(√(x(x+(1/x)+1)))))=1 (1/( 1+(√x) (√(x+(1/x)−1))))+(x/( 1+(√x) (√(x+(1/x)+1)) ))=1 Let x+(1/x)+1=y^2 x+(1/x)−1=y^2 −2 (1/( 1+(√x) (√(y^2 −2))))+(x/( 1+y(√x) ))=1 1−(1/( 1+(√x) (√(y^2 −2))))=(x/( 1+y(√x) )) ((1+(√x) (√(y^2 −2)) −1)/(1+(√x) (√(y^2 −2))))=(x/( 1+y(√x) )) (((√x) (√(y^2 −2)) )/(1+(√x) (√(y^2 −2))))=(x/( 1+y(√x) )) ((1+(√x) (√(y^2 −2)))/( (√x) (√(y^2 −2)) ))=((1+y(√x) )/x) (1/( (√x) (√(y^2 −2)) ))+1=(1/x)+(y/( (√x))) (1/( (√x) (√(y^2 −2)) ))−(y/( (√x)))=(1/x)−1=((1−x)/x) (1/( (√(y^2 −2))))−y=((1−x)/( (√x))) ((1−y(√(y^2 −2)) )/( (√(y^2 −2))))=((1−x)/( (√x))) (((1−y(√(y^2 −2)) )/( (√(y^2 −2)))))^2 =(((1−x)/( (√x))))^2 ((1+y^2 (y^2 −2)−2y(√(y^2 −2)))/(y^2 −2))=((1+x^2 −2x)/x) ((1+y^2 (y^2 −2)−2y(√(y^2 −2)))/(y^2 −2))=x+(1/x)−2 ((1+y^2 (y^2 −2)−2y(√(y^2 −2)))/(y^2 −2))=x+(1/x)+1−3 ((1+y^2 (y^2 −2)−2y(√(y^2 −2)))/(y^2 −2))=y^2 −3 1+y^4 −2y^2 −2y(√(y^2 −2)) =(y^2 −3)(y^2 −2) 1+y^4 −2y^2 −2y(√(y^2 −2)) =y^4 −5y^2 +6 2y(√(y^2 −2)) =3y^2 −5 4y^2 (y^2 −2)=9y^4 −30y^2 +25 5y^4 −22y^2 +25=0 y^2 =((22±(√(484−500)))/(10))=((22±4i)/(10))=((11±2i)/5) ▶(x/(x^( 2) +1))=(1/(x+(1/x)))=(1/(x+(1/x)+1−1))=(1/(y^2 −1)) =(1/(((11±2i)/5)−1))=(1/((6±2i)/5))=(5/(6±2i))∙((6∓2i)/(6∓2i)) =((5(6∓2i))/(36+4))=((6∓2i)/8)=((3±i)/4)

$$\:\:\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{\mathrm{1}−{x}+{x}^{\:\mathrm{2}} }}\:+\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{1}+{x}+{x}^{\:\mathrm{2}} }}=\mathrm{1} \\ $$$$\frac{{x}}{{x}^{\:\mathrm{2}} +\mathrm{1}}=? \\ $$$$\:\:\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{{x}\left({x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)}}\:+\frac{{x}}{\mathrm{1}+\sqrt{{x}\left({x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}\right)}}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{{x}}\:\sqrt{{x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}}}+\frac{{x}}{\:\mathrm{1}+\sqrt{{x}}\:\sqrt{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\:}=\mathrm{1} \\ $$$${Let}\:{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}={y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:{x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}={y}^{\mathrm{2}} −\mathrm{2} \\ $$$$\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}+\frac{{x}}{\:\mathrm{1}+{y}\sqrt{{x}}\:\:}=\mathrm{1} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}=\frac{{x}}{\:\mathrm{1}+{y}\sqrt{{x}}\:\:} \\ $$$$\frac{\mathrm{1}+\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:−\mathrm{1}}{\mathrm{1}+\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}=\frac{{x}}{\:\mathrm{1}+{y}\sqrt{{x}}\:\:} \\ $$$$\frac{\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:}{\mathrm{1}+\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}=\frac{{x}}{\:\mathrm{1}+{y}\sqrt{{x}}\:\:} \\ $$$$\frac{\mathrm{1}+\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}{\:\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:}=\frac{\mathrm{1}+{y}\sqrt{{x}}\:}{{x}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:}+\mathrm{1}=\frac{\mathrm{1}}{{x}}+\frac{{y}}{\:\sqrt{{x}}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{x}}\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:}−\frac{{y}}{\:\sqrt{{x}}}=\frac{\mathrm{1}}{{x}}−\mathrm{1}=\frac{\mathrm{1}−{x}}{{x}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}−{y}=\frac{\mathrm{1}−{x}}{\:\sqrt{{x}}} \\ $$$$\frac{\mathrm{1}−{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}=\frac{\mathrm{1}−{x}}{\:\sqrt{{x}}} \\ $$$$\left(\frac{\mathrm{1}−{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}−{x}}{\:\sqrt{{x}}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}+{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}{{y}^{\mathrm{2}} −\mathrm{2}}=\frac{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x}}{{x}} \\ $$$$\frac{\mathrm{1}+{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}{{y}^{\mathrm{2}} −\mathrm{2}}={x}+\frac{\mathrm{1}}{{x}}−\mathrm{2} \\ $$$$\frac{\mathrm{1}+{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}{{y}^{\mathrm{2}} −\mathrm{2}}={x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}−\mathrm{3} \\ $$$$\frac{\mathrm{1}+{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}{{y}^{\mathrm{2}} −\mathrm{2}}={y}^{\mathrm{2}} −\mathrm{3} \\ $$$$\mathrm{1}+{y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:=\left({y}^{\mathrm{2}} −\mathrm{3}\right)\left({y}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$$\mathrm{1}+{y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:={y}^{\mathrm{4}} −\mathrm{5}{y}^{\mathrm{2}} +\mathrm{6} \\ $$$$\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:=\mathrm{3}{y}^{\mathrm{2}} −\mathrm{5} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)=\mathrm{9}{y}^{\mathrm{4}} −\mathrm{30}{y}^{\mathrm{2}} +\mathrm{25} \\ $$$$\mathrm{5}{y}^{\mathrm{4}} −\mathrm{22}{y}^{\mathrm{2}} +\mathrm{25}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{22}\pm\sqrt{\mathrm{484}−\mathrm{500}}}{\mathrm{10}}=\frac{\mathrm{22}\pm\mathrm{4}\boldsymbol{{i}}}{\mathrm{10}}=\frac{\mathrm{11}\pm\mathrm{2}\boldsymbol{{i}}}{\mathrm{5}} \\ $$$$\:\: \\ $$$$\blacktriangleright\frac{{x}}{{x}^{\:\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}}=\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}−\mathrm{1}}=\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:=\frac{\mathrm{1}}{\frac{\mathrm{11}\pm\mathrm{2}\boldsymbol{{i}}}{\mathrm{5}}−\mathrm{1}}=\frac{\mathrm{1}}{\frac{\mathrm{6}\pm\mathrm{2}{i}}{\mathrm{5}}}=\frac{\mathrm{5}}{\mathrm{6}\pm\mathrm{2}{i}}\centerdot\frac{\mathrm{6}\mp\mathrm{2}{i}}{\mathrm{6}\mp\mathrm{2}{i}} \\ $$$$=\frac{\mathrm{5}\left(\mathrm{6}\mp\mathrm{2}{i}\right)}{\mathrm{36}+\mathrm{4}}=\frac{\mathrm{6}\mp\mathrm{2}{i}}{\mathrm{8}}=\frac{\mathrm{3}\pm{i}}{\mathrm{4}} \\ $$

Commented by manxsol last updated on 16/Dec/22

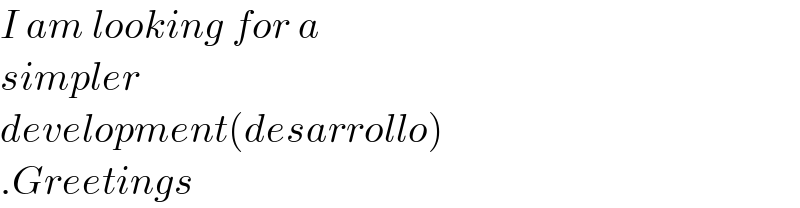
I am looking for a simpler development(desarrollo) .Greetings

$${I}\:{am}\:{looking}\:{for}\:{a}\: \\ $$$${simpler}\: \\ $$$${development}\left({desarrollo}\right) \\ $$$$.{Greetings} \\ $$

Commented by manxsol last updated on 16/Dec/22

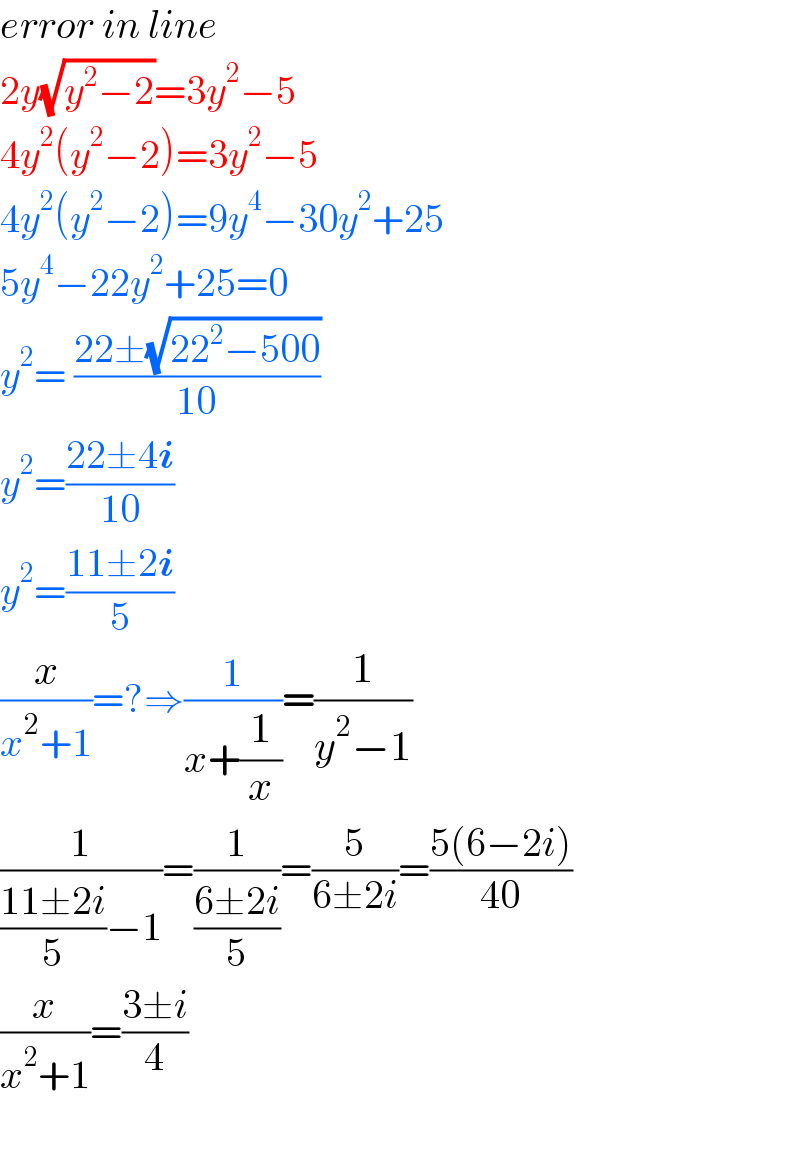
error in line 2y(√(y^2 −2))=3y^2 −5 4y^2 (y^2 −2)=3y^2 −5 4y^2 (y^2 −2)=9y^4 −30y^2 +25 5y^4 −22y^2 +25=0 y^2 = ((22±(√(22^2 −500)))/(10)) y^2 =((22±4i)/(10)) y^2 =((11±2i)/5) (x/(x^2 +1))=?⇒(1/(x+(1/x)))=(1/(y^2 −1)) (1/(((11±2i)/5)−1))=(1/((6±2i)/5))=(5/(6±2i))=((5(6−2i))/(40)) (x/(x^2 +1))=((3±i)/4)

$${error}\:{in}\:{line} \\ $$$$\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}=\mathrm{3}{y}^{\mathrm{2}} −\mathrm{5} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)=\mathrm{3}{y}^{\mathrm{2}} −\mathrm{5} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)=\mathrm{9}{y}^{\mathrm{4}} −\mathrm{30}{y}^{\mathrm{2}} +\mathrm{25} \\ $$$$\mathrm{5}{y}^{\mathrm{4}} −\mathrm{22}{y}^{\mathrm{2}} +\mathrm{25}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} =\:\frac{\mathrm{22}\pm\sqrt{\mathrm{22}^{\mathrm{2}} −\mathrm{500}}}{\mathrm{10}} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{22}\pm\mathrm{4}\boldsymbol{{i}}}{\mathrm{10}} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{11}\pm\mathrm{2}\boldsymbol{{i}}}{\mathrm{5}} \\ $$$$\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}=?\Rightarrow\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}}=\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\frac{\mathrm{11}\pm\mathrm{2}{i}}{\mathrm{5}}−\mathrm{1}}=\frac{\mathrm{1}}{\frac{\mathrm{6}\pm\mathrm{2}{i}}{\mathrm{5}}}=\frac{\mathrm{5}}{\mathrm{6}\pm\mathrm{2}{i}}=\frac{\mathrm{5}\left(\mathrm{6}−\mathrm{2}{i}\right)}{\mathrm{40}} \\ $$$$\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{3}\pm{i}}{\mathrm{4}} \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 15/Dec/22

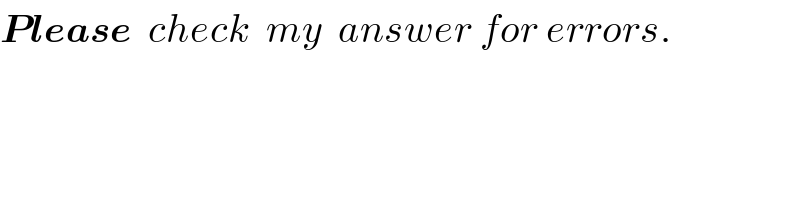
Please check my answer for errors.

$$\boldsymbol{{Please}}\:\:{check}\:\:{my}\:\:{answer}\:{for}\:{errors}. \\ $$

Commented by mnjuly1970 last updated on 15/Dec/22

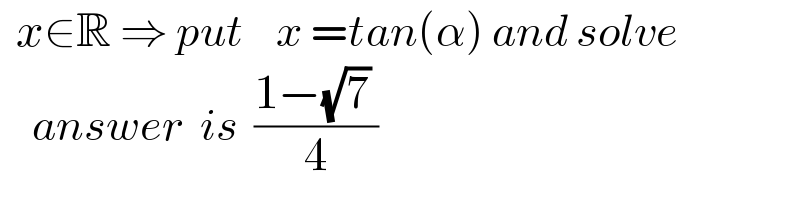
x∈R ⇒ put x =tan(α) and solve answer is ((1−(√7) )/4)

$$\:\:{x}\in\mathbb{R}\:\Rightarrow\:{put}\:\:\:\:{x}\:={tan}\left(\alpha\right)\:{and}\:{solve} \\ $$$$\:\:\:\:{answer}\:\:{is}\:\:\frac{\mathrm{1}−\sqrt{\mathrm{7}}\:}{\mathrm{4}} \\ $$

Commented by mr W last updated on 15/Dec/22

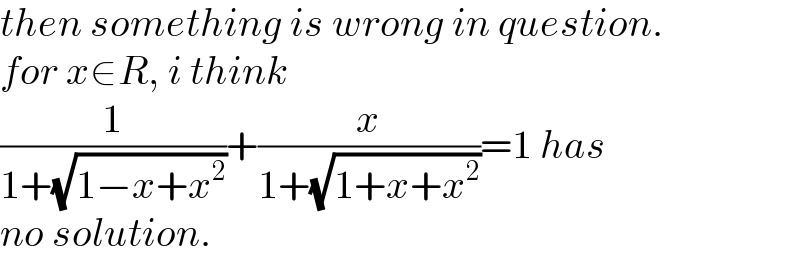
then something is wrong in question. for x∈R, i think (1/(1+(√(1−x+x^2 ))))+(x/(1+(√(1+x+x^2 ))))=1 has no solution.

$${then}\:{something}\:{is}\:{wrong}\:{in}\:{question}. \\ $$$${for}\:{x}\in{R},\:{i}\:{think} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} }}+\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }}=\mathrm{1}\:{has} \\ $$$${no}\:{solution}. \\ $$

Commented by ellenpaulisrae last updated on 15/Dec/22

hello

$${hello} \\ $$

Commented by Frix last updated on 15/Dec/22

Yes, there′s no real solution for the given equation.

$$\mathrm{Yes},\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{equation}. \\ $$

Commented by Rasheed.Sindhi last updated on 16/Dec/22

ThanX manxsol sir! I′m going to correct my answer. The approach is correct although lengthy! I′ll wait for your simpler approach.But mean while mnjuly sir has changed his question and very sorry to say that he did this without any intimation! Anyway thanks again!

$$\mathcal{T}{han}\mathcal{X}\:{manxsol}\:\boldsymbol{{sir}}!\: \\ $$$${I}'{m}\:{going}\:{to}\:{correct}\:{my}\:{answer}. \\ $$$$\mathcal{T}{he}\:{approach}\:{is}\:{correct}\:{although} \\ $$$${lengthy}!\:{I}'{ll}\:{wait}\:{for}\:{your}\:{simpler} \\ $$$${approach}.{But}\:{mean}\:{while}\:{mnjuly}\:{sir} \\ $$$$\:{has}\:{changed}\:{his}\:{question}\:{and}\:{very}\: \\ $$$${sorry}\:{to}\:{say}\:{that}\:{he}\:{did}\:{this}\:{without} \\ $$$$\:{any}\:\boldsymbol{{intimation}}!\:{Anyway}\:\mathrm{than}\Bbbk\mathrm{s}\: \\ $$$$\mathrm{again}! \\ $$

Commented by mnjuly1970 last updated on 16/Dec/22

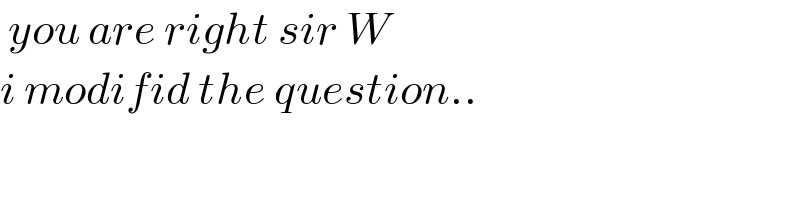
you are right sir W i modifid the question..

$$\:{you}\:{are}\:{right}\:{sir}\:{W} \\ $$$${i}\:{modifid}\:{the}\:{question}.. \\ $$

Answered by Rasheed.Sindhi last updated on 16/Dec/22

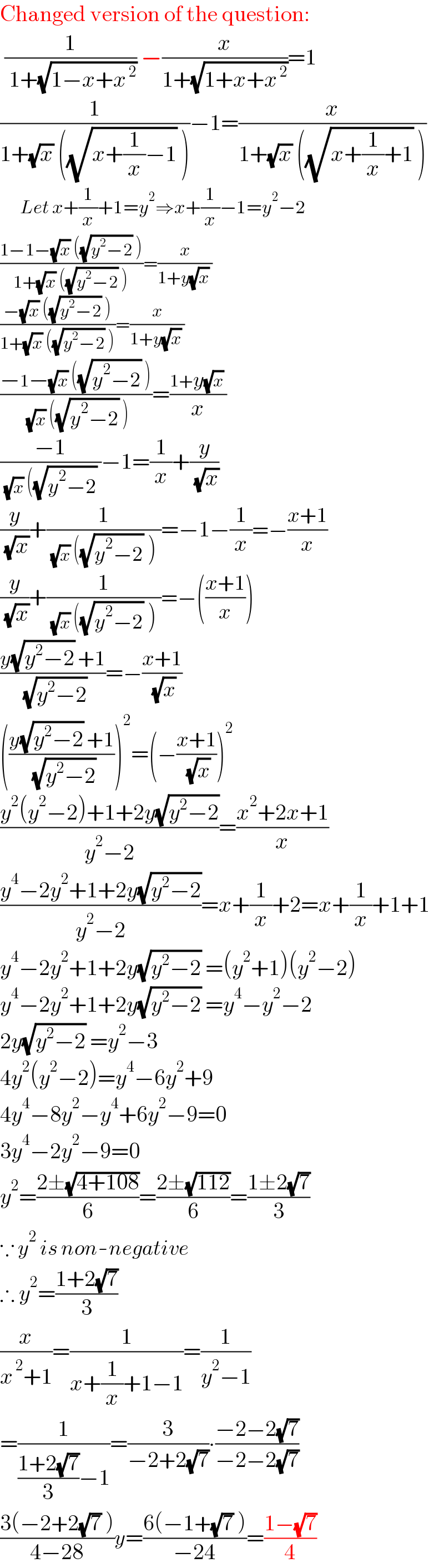
Changed version of the question: (1/( 1+(√(1−x+x^( 2) )))) −(x/(1+(√(1+x+x^( 2) ))))=1 (1/(1+(√x) ((√(x+(1/x)−1)) )))−1=(x/(1+(√x) ((√(x+(1/x)+1)) ))) Let x+(1/x)+1=y^2 ⇒x+(1/x)−1=y^2 −2 ((1−1−(√x) ((√(y^2 −2)) ))/(1+(√x) ((√(y^2 −2)) )))=(x/(1+y(√x) )) ((−(√x) ((√(y^2 −2)) ))/(1+(√x) ((√(y^2 −2)) )))=(x/(1+y(√x) )) ((−1−(√x) ((√(y^2 −2)) ))/( (√x) ((√(y^2 −2)) )))=((1+y(√x) )/x) ((−1)/( (√x) ((√(y^2 −2)) ))−1=(1/x)+(y/( (√x))) (y/( (√x)))+(1/( (√x) ((√(y^2 −2)) ) ))=−1−(1/x)=−((x+1)/x) (y/( (√x)))+(1/( (√x) ((√(y^2 −2)) ) ))=−(((x+1)/x)) ((y(√(y^2 −2)) +1)/( (√(y^2 −2))))=−((x+1)/( (√x))) (((y(√(y^2 −2)) +1)/( (√(y^2 −2)))))^2 =(−((x+1)/( (√x))))^2 ((y^2 (y^2 −2)+1+2y(√(y^2 −2)))/(y^2 −2))=((x^2 +2x+1)/x) ((y^4 −2y^2 +1+2y(√(y^2 −2)))/(y^2 −2))=x+(1/x)+2=x+(1/x)+1+1 y^4 −2y^2 +1+2y(√(y^2 −2)) =(y^2 +1)(y^2 −2) y^4 −2y^2 +1+2y(√(y^2 −2)) =y^4 −y^2 −2 2y(√(y^2 −2)) =y^2 −3 4y^2 (y^2 −2)=y^4 −6y^2 +9 4y^4 −8y^2 −y^4 +6y^2 −9=0 3y^4 −2y^2 −9=0 y^2 =((2±(√(4+108)))/6)=((2±(√(112)))/6)=((1±2(√7))/3) ∵ y^2 is non-negative ∴ y^2 =((1+2(√7))/3) (x/(x^( 2) +1))=(1/(x+(1/x)+1−1))=(1/(y^2 −1)) =(1/(((1+2(√7))/3)−1))=(3/(−2+2(√7)))∙((−2−2(√7))/(−2−2(√7))) ((3(−2+2(√7) ))/(4−28))y=((6(−1+(√7) ))/(−24))=((1−(√7))/4)

$$\mathrm{Changed}\:\mathrm{version}\:\mathrm{of}\:\mathrm{the}\:\mathrm{question}: \\ $$$$\:\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{\mathrm{1}−{x}+{x}^{\:\mathrm{2}} }}\:−\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{1}+{x}+{x}^{\:\mathrm{2}} }}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\sqrt{{x}}\:\left(\sqrt{{x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}}\:\right)}−\mathrm{1}=\frac{{x}}{\mathrm{1}+\sqrt{{x}}\:\left(\sqrt{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\:\right)} \\ $$$$\:\:\:\:\:\:{Let}\:{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}={y}^{\mathrm{2}} \Rightarrow{x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}={y}^{\mathrm{2}} −\mathrm{2} \\ $$$$\frac{\mathrm{1}−\mathrm{1}−\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right)}{\mathrm{1}+\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right)}=\frac{{x}}{\mathrm{1}+{y}\sqrt{{x}}\:} \\ $$$$\frac{−\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right)}{\mathrm{1}+\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right)}=\frac{{x}}{\mathrm{1}+{y}\sqrt{{x}}\:} \\ $$$$\frac{−\mathrm{1}−\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right)}{\:\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right)}=\frac{\mathrm{1}+{y}\sqrt{{x}}\:}{{x}} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right.}−\mathrm{1}=\frac{\mathrm{1}}{{x}}+\frac{{y}}{\:\sqrt{{x}}} \\ $$$$\frac{{y}}{\:\sqrt{{x}}}+\frac{\mathrm{1}}{\:\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right)\:}=−\mathrm{1}−\frac{\mathrm{1}}{{x}}=−\frac{{x}+\mathrm{1}}{{x}} \\ $$$$\frac{{y}}{\:\sqrt{{x}}}+\frac{\mathrm{1}}{\:\sqrt{{x}}\:\left(\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:\right)\:}=−\left(\frac{{x}+\mathrm{1}}{{x}}\right) \\ $$$$\frac{{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}=−\frac{{x}+\mathrm{1}}{\:\sqrt{{x}}} \\ $$$$\left(\frac{{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}\right)^{\mathrm{2}} =\left(−\frac{{x}+\mathrm{1}}{\:\sqrt{{x}}}\right)^{\mathrm{2}} \\ $$$$\frac{{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)+\mathrm{1}+\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}{{y}^{\mathrm{2}} −\mathrm{2}}=\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{{x}} \\ $$$$\frac{{y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}}{{y}^{\mathrm{2}} −\mathrm{2}}={x}+\frac{\mathrm{1}}{{x}}+\mathrm{2}={x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}+\mathrm{1} \\ $$$${y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:=\left({y}^{\mathrm{2}} +\mathrm{1}\right)\left({y}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$${y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:={y}^{\mathrm{4}} −{y}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{2}{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{2}}\:={y}^{\mathrm{2}} −\mathrm{3} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} \left({y}^{\mathrm{2}} −\mathrm{2}\right)={y}^{\mathrm{4}} −\mathrm{6}{y}^{\mathrm{2}} +\mathrm{9} \\ $$$$\mathrm{4}{y}^{\mathrm{4}} −\mathrm{8}{y}^{\mathrm{2}} −{y}^{\mathrm{4}} +\mathrm{6}{y}^{\mathrm{2}} −\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{3}{y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{2}} −\mathrm{9}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} =\frac{\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{108}}}{\mathrm{6}}=\frac{\mathrm{2}\pm\sqrt{\mathrm{112}}}{\mathrm{6}}=\frac{\mathrm{1}\pm\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}} \\ $$$$\because\:{y}^{\mathrm{2}} \:{is}\:{non}-{negative} \\ $$$$\therefore\:{y}^{\mathrm{2}} =\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}} \\ $$$$\frac{{x}}{{x}^{\:\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}−\mathrm{1}}=\frac{\mathrm{1}}{{y}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}}−\mathrm{1}}=\frac{\mathrm{3}}{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{7}}}\centerdot\frac{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{7}}}{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{7}}} \\ $$$$\frac{\mathrm{3}\left(−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{7}}\:\right)}{\mathrm{4}−\mathrm{28}}{y}=\frac{\mathrm{6}\left(−\mathrm{1}+\sqrt{\mathrm{7}}\:\right)}{−\mathrm{24}}=\frac{\mathrm{1}−\sqrt{\mathrm{7}}}{\mathrm{4}} \\ $$

Commented by mnjuly1970 last updated on 16/Dec/22

very nice solution sir Rasheed .thanks alot for your effort. that was my mistake⟨typo⟩ i modified it.

$${very}\:{nice}\:{solution} \\ $$$${sir}\:{Rasheed}\:.{thanks}\:{alot} \\ $$$${for}\:{your}\:{effort}. \\ $$$$\:\:{that}\:{was}\:{my}\:{mistake}\langle{typo}\rangle \\ $$$$\:\:\:{i}\:{modified}\:{it}. \\ $$

Answered by Rasheed.Sindhi last updated on 17/Dec/22

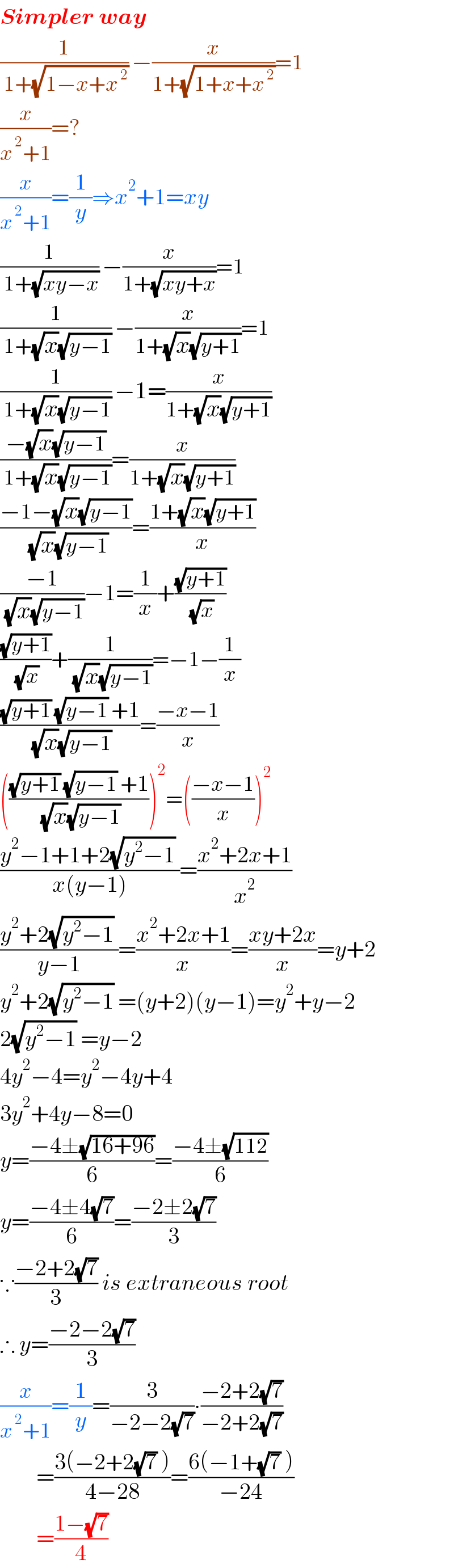
Simpler way (1/( 1+(√(1−x+x^( 2) )))) −(x/(1+(√(1+x+x^( 2) ))))=1 (x/(x^( 2) +1))=? (x/(x^( 2) +1))=(1/y)⇒x^2 +1=xy (1/( 1+(√(xy−x)))) −(x/(1+(√(xy+x))))=1 (1/( 1+(√x)(√(y−1)))) −(x/(1+(√x)(√(y+1))))=1 (1/( 1+(√x)(√(y−1)))) −1=(x/(1+(√x)(√(y+1)))) ((−(√x)(√(y−1)))/( 1+(√x)(√(y−1))))=(x/(1+(√x)(√(y+1)))) ((−1−(√x)(√(y−1)))/( (√x)(√(y−1))))=((1+(√x)(√(y+1)))/x) ((−1)/( (√x)(√(y−1))))−1=(1/x)+((√(y+1))/( (√x))) ((√(y+1))/( (√x)))+(1/( (√x)(√(y−1))))=−1−(1/x) (((√(y+1)) (√(y−1)) +1)/( (√x)(√(y−1))))=((−x−1)/x) ((((√(y+1)) (√(y−1)) +1)/( (√x)(√(y−1)))))^2 =(((−x−1)/x))^2 ((y^2 −1+1+2(√(y^2 −1)) )/(x(y−1)))=((x^2 +2x+1)/x^2 ) ((y^2 +2(√(y^2 −1)) )/(y−1))=((x^2 +2x+1)/x)=((xy+2x)/x)=y+2 y^2 +2(√(y^2 −1)) =(y+2)(y−1)=y^2 +y−2 2(√(y^2 −1)) =y−2 4y^2 −4=y^2 −4y+4 3y^2 +4y−8=0 y=((−4±(√(16+96)))/6)=((−4±(√(112)))/6) y=((−4±4(√7))/6)=((−2±2(√7))/3) ∵((−2+2(√7))/3) is extraneous root ∴ y=((−2−2(√7))/3) (x/(x^( 2) +1))=(1/y)=(3/(−2−2(√7)))∙((−2+2(√7))/(−2+2(√7))) =((3(−2+2(√7) ))/(4−28))=((6(−1+(√7) ))/(−24)) =((1−(√7))/4)

$$\boldsymbol{{Simpler}}\:\boldsymbol{{way}} \\ $$$$\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{\mathrm{1}−{x}+{x}^{\:\mathrm{2}} }}\:−\frac{{x}}{\mathrm{1}+\sqrt{\mathrm{1}+{x}+{x}^{\:\mathrm{2}} }}=\mathrm{1} \\ $$$$\frac{{x}}{{x}^{\:\mathrm{2}} +\mathrm{1}}=? \\ $$$$\frac{{x}}{{x}^{\:\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{y}}\Rightarrow{x}^{\mathrm{2}} +\mathrm{1}={xy} \\ $$$$\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{{xy}−{x}}}\:−\frac{{x}}{\mathrm{1}+\sqrt{{xy}+{x}}}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}\:−\frac{{x}}{\mathrm{1}+\sqrt{{x}}\sqrt{{y}+\mathrm{1}}}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}\:−\mathrm{1}=\frac{{x}}{\mathrm{1}+\sqrt{{x}}\sqrt{{y}+\mathrm{1}}} \\ $$$$\frac{−\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}{\:\mathrm{1}+\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}=\frac{{x}}{\mathrm{1}+\sqrt{{x}}\sqrt{{y}+\mathrm{1}}} \\ $$$$\frac{−\mathrm{1}−\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}{\:\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}=\frac{\mathrm{1}+\sqrt{{x}}\sqrt{{y}+\mathrm{1}}}{{x}} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}−\mathrm{1}=\frac{\mathrm{1}}{{x}}+\frac{\sqrt{{y}+\mathrm{1}}}{\:\sqrt{{x}}} \\ $$$$\frac{\sqrt{{y}+\mathrm{1}}}{\:\sqrt{{x}}}+\frac{\mathrm{1}}{\:\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}=−\mathrm{1}−\frac{\mathrm{1}}{{x}} \\ $$$$\frac{\sqrt{{y}+\mathrm{1}}\:\sqrt{{y}−\mathrm{1}}\:+\mathrm{1}}{\:\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}=\frac{−{x}−\mathrm{1}}{{x}} \\ $$$$\left(\frac{\sqrt{{y}+\mathrm{1}}\:\sqrt{{y}−\mathrm{1}}\:+\mathrm{1}}{\:\sqrt{{x}}\sqrt{{y}−\mathrm{1}}}\right)^{\mathrm{2}} =\left(\frac{−{x}−\mathrm{1}}{{x}}\right)^{\mathrm{2}} \\ $$$$\frac{{y}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}+\mathrm{2}\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:}{{x}\left({y}−\mathrm{1}\right)}=\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\frac{{y}^{\mathrm{2}} +\mathrm{2}\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:}{{y}−\mathrm{1}}=\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{{x}}=\frac{{xy}+\mathrm{2}{x}}{{x}}={y}+\mathrm{2} \\ $$$${y}^{\mathrm{2}} +\mathrm{2}\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:=\left({y}+\mathrm{2}\right)\left({y}−\mathrm{1}\right)={y}^{\mathrm{2}} +{y}−\mathrm{2} \\ $$$$\mathrm{2}\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:={y}−\mathrm{2} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}={y}^{\mathrm{2}} −\mathrm{4}{y}+\mathrm{4} \\ $$$$\mathrm{3}{y}^{\mathrm{2}} +\mathrm{4}{y}−\mathrm{8}=\mathrm{0} \\ $$$${y}=\frac{−\mathrm{4}\pm\sqrt{\mathrm{16}+\mathrm{96}}}{\mathrm{6}}=\frac{−\mathrm{4}\pm\sqrt{\mathrm{112}}}{\mathrm{6}} \\ $$$${y}=\frac{−\mathrm{4}\pm\mathrm{4}\sqrt{\mathrm{7}}}{\mathrm{6}}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}} \\ $$$$\because\frac{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}}\:{is}\:{extraneous}\:{root} \\ $$$$\therefore\:{y}=\frac{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}} \\ $$$$\frac{{x}}{{x}^{\:\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{y}}=\frac{\mathrm{3}}{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{7}}}\centerdot\frac{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{7}}}{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{7}}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{3}\left(−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{7}}\:\right)}{\mathrm{4}−\mathrm{28}}=\frac{\mathrm{6}\left(−\mathrm{1}+\sqrt{\mathrm{7}}\:\right)}{−\mathrm{24}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}−\sqrt{\mathrm{7}}}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com