
Question Number 186803 by ajfour last updated on 10/Feb/23

Answered by ajfour last updated on 10/Feb/23
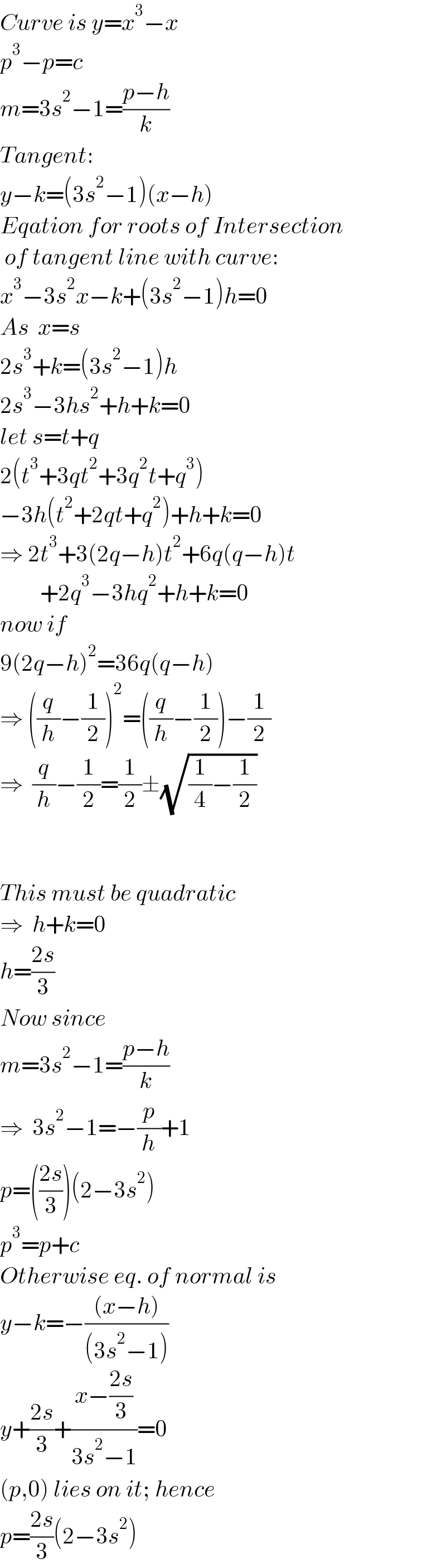
$${Curve}\:{is}\:{y}={x}^{\mathrm{3}} −{x} \\ $$$${p}^{\mathrm{3}} −{p}={c} \\ $$$${m}=\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}=\frac{{p}−{h}}{{k}} \\ $$$${Tangent}: \\ $$$${y}−{k}=\left(\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}\right)\left({x}−{h}\right) \\ $$$${Eqation}\:{for}\:{roots}\:{of}\:{Intersection} \\ $$$$\:{of}\:{tangent}\:{line}\:{with}\:{curve}: \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{s}^{\mathrm{2}} {x}−{k}+\left(\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}\right){h}=\mathrm{0} \\ $$$${As}\:\:{x}={s} \\ $$$$\mathrm{2}{s}^{\mathrm{3}} +{k}=\left(\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}\right){h} \\ $$$$\mathrm{2}{s}^{\mathrm{3}} −\mathrm{3}{hs}^{\mathrm{2}} +{h}+{k}=\mathrm{0} \\ $$$${let}\:{s}={t}+{q} \\ $$$$\mathrm{2}\left({t}^{\mathrm{3}} +\mathrm{3}{qt}^{\mathrm{2}} +\mathrm{3}{q}^{\mathrm{2}} {t}+{q}^{\mathrm{3}} \right) \\ $$$$−\mathrm{3}{h}\left({t}^{\mathrm{2}} +\mathrm{2}{qt}+{q}^{\mathrm{2}} \right)+{h}+{k}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}{t}^{\mathrm{3}} +\mathrm{3}\left(\mathrm{2}{q}−{h}\right){t}^{\mathrm{2}} +\mathrm{6}{q}\left({q}−{h}\right){t} \\ $$$$\:\:\:\:\:\:\:\:\:+\mathrm{2}{q}^{\mathrm{3}} −\mathrm{3}{hq}^{\mathrm{2}} +{h}+{k}=\mathrm{0} \\ $$$${now}\:{if} \\ $$$$\mathrm{9}\left(\mathrm{2}{q}−{h}\right)^{\mathrm{2}} =\mathrm{36}{q}\left({q}−{h}\right) \\ $$$$\Rightarrow\:\left(\frac{{q}}{{h}}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{{q}}{{h}}−\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{{q}}{{h}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$$${This}\:{must}\:{be}\:{quadratic} \\ $$$$\Rightarrow\:\:{h}+{k}=\mathrm{0} \\ $$$${h}=\frac{\mathrm{2}{s}}{\mathrm{3}} \\ $$$${Now}\:{since} \\ $$$${m}=\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}=\frac{{p}−{h}}{{k}} \\ $$$$\Rightarrow\:\:\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}=−\frac{{p}}{{h}}+\mathrm{1} \\ $$$${p}=\left(\frac{\mathrm{2}{s}}{\mathrm{3}}\right)\left(\mathrm{2}−\mathrm{3}{s}^{\mathrm{2}} \right) \\ $$$${p}^{\mathrm{3}} ={p}+{c} \\ $$$${Otherwise}\:{eq}.\:{of}\:{normal}\:{is} \\ $$$${y}−{k}=−\frac{\left({x}−{h}\right)}{\left(\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$${y}+\frac{\mathrm{2}{s}}{\mathrm{3}}+\frac{{x}−\frac{\mathrm{2}{s}}{\mathrm{3}}}{\mathrm{3}{s}^{\mathrm{2}} −\mathrm{1}}=\mathrm{0} \\ $$$$\left({p},\mathrm{0}\right)\:{lies}\:{on}\:{it};\:{hence} \\ $$$${p}=\frac{\mathrm{2}{s}}{\mathrm{3}}\left(\mathrm{2}−\mathrm{3}{s}^{\mathrm{2}} \right) \\ $$
