
Question Number 190987 by Rupesh123 last updated on 15/Apr/23
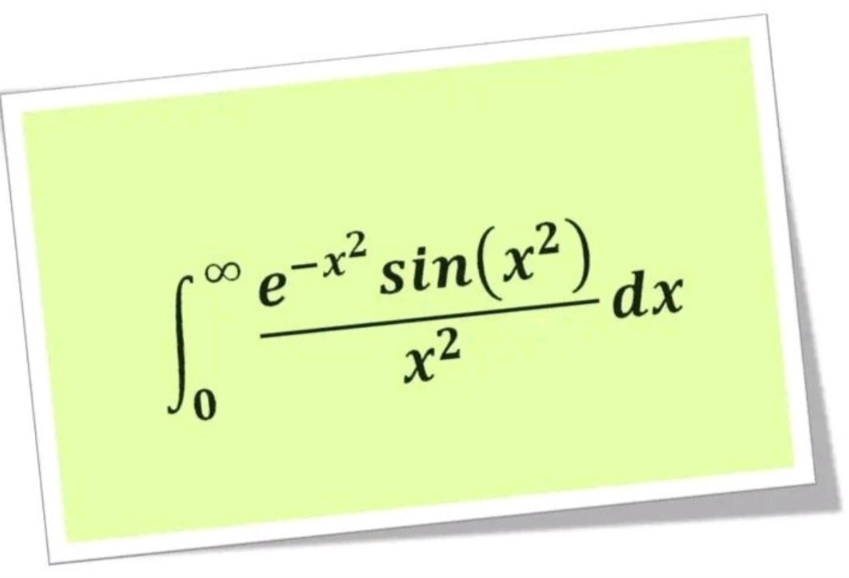
Answered by 07049753053 last updated on 16/Apr/23
![let x^2 =u dx=(du/(2(√u))) (1/2)∫_0 ^∞ ((e^(−u) sin(u))/(u(√u)))du=(1/2)∫_0 ^∞ u^(−(3/2)) e^(−u) sin(u)du by euler′s formula sin(u)=Im(e^(iu) ) (1/2)Im∫_0 ^∞ u^(−(3/2)) e^(−u(i−1)) du let u(i−1)=k u=(k/(i−1)) du=(dk/(i−1)) (1/2)Im((1/((i−1)^(−(1/2)) ))∫_0 ^∞ k^(−(3/2)) e^(−k) dk) (1/2)Im((1/((i−1)^(−(1/2)) ))𝚪(−(1/2)))=(1/2)Im((√((1−i))))𝚪(−(1/2)) (1/2)[(√𝛑)(√((1/2)−(1/( (√2)))))]=((√𝛑)/2)(√(((√2)−2)/(2(√2))))≈0.806625... Small Laplace](Q191044.png)
$$\boldsymbol{\mathrm{let}}\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\boldsymbol{\mathrm{u}}\:\boldsymbol{\mathrm{dx}}=\frac{\boldsymbol{\mathrm{du}}}{\mathrm{2}\sqrt{\boldsymbol{\mathrm{u}}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{u}}} \boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{u}}\right)}{\boldsymbol{\mathrm{u}}\sqrt{\boldsymbol{\mathrm{u}}}}\boldsymbol{\mathrm{du}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{u}}^{−\frac{\mathrm{3}}{\mathrm{2}}} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{u}}} \boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{u}}\right)\boldsymbol{\mathrm{du}} \\ $$$$\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{euler}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{formula}} \\ $$$$\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{u}}\right)=\boldsymbol{\mathcal{I}{m}}\left(\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{iu}}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathcal{I}{m}}\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{u}}^{−\frac{\mathrm{3}}{\mathrm{2}}} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{u}}\left(\boldsymbol{\mathrm{i}}−\mathrm{1}\right)} \boldsymbol{\mathrm{du}} \\ $$$$\boldsymbol{\mathrm{let}}\:\boldsymbol{\mathrm{u}}\left(\boldsymbol{\mathrm{i}}−\mathrm{1}\right)=\boldsymbol{\mathrm{k}}\:\boldsymbol{\mathrm{u}}=\frac{\boldsymbol{\mathrm{k}}}{\boldsymbol{\mathrm{i}}−\mathrm{1}}\:\boldsymbol{\mathrm{du}}=\frac{\boldsymbol{\mathrm{dk}}}{\boldsymbol{\mathrm{i}}−\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathcal{I}{m}}\left(\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{i}}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} }\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{k}}^{−\frac{\mathrm{3}}{\mathrm{2}}} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{k}}} \boldsymbol{\mathrm{dk}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathcal{I}\mathrm{m}}\left(\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{i}}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} }\boldsymbol{\Gamma}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathcal{I}\mathrm{m}}\left(\sqrt{\left(\mathrm{1}−{i}\right)}\right)\boldsymbol{\Gamma}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\sqrt{\boldsymbol{\pi}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\right]=\frac{\sqrt{\boldsymbol{\pi}}}{\mathrm{2}}\sqrt{\frac{\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}}\approx\mathrm{0}.\mathrm{806625}... \\ $$$$\boldsymbol{\mathcal{S}{mall}}\:\boldsymbol{{Laplace}} \\ $$
