
Question Number 19271 by Joel577 last updated on 08/Aug/17
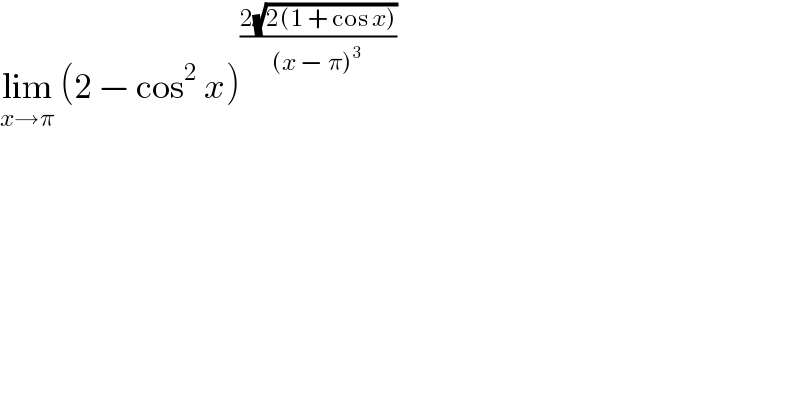
$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\left(\mathrm{2}\:−\:\mathrm{cos}^{\mathrm{2}} \:{x}\right)^{\frac{\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}\:+\:\mathrm{cos}\:{x}\right)}}{\left({x}\:−\:\pi\right)^{\mathrm{3}} }} \\ $$
Answered by ajfour last updated on 09/Aug/17
![=lim_(x→π) {[1+sin^2 (π−x)]^(1/(sin^2 (π−x))) }^(4cos ((x/2))×((sin^2 (π−x))/((π−x)^2 ))×((−1)/((π−x)))) =e^(lim_(x→π) ∣4sin ((π/2)−(x/2))∣×((sin^2 (π−x))/((π−x)^2 ))×((−1)/((π−x)))) =e^(−lim_(x→π) ((∣4sin ((π/2)−(x/2))∣)/(2((π/2)−(x/2))))) R.H.L. =e^2 ; L.H.L. =e^(−2) =(1/e^2 ) . so the limit dont exist at x=π .](Q19274.png)
$$=\underset{{x}\rightarrow\pi} {\mathrm{lim}}\left\{\left[\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\pi−\mathrm{x}\right)\right]^{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \left(\pi−\mathrm{x}\right)}} \right\}^{\mathrm{4cos}\:\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)×\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\pi−\mathrm{x}\right)}{\left(\pi−\mathrm{x}\right)^{\mathrm{2}} }×\frac{−\mathrm{1}}{\left(\pi−\mathrm{x}\right)}} \\ $$$$=\mathrm{e}^{\underset{{x}\rightarrow\pi} {\mathrm{lim}}\mid\mathrm{4sin}\:\:\:\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\right)\mid×\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\pi−\mathrm{x}\right)}{\left(\pi−\mathrm{x}\right)^{\mathrm{2}} }×\frac{−\mathrm{1}}{\left(\pi−\mathrm{x}\right)}} \\ $$$$=\mathrm{e}^{−\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mid\mathrm{4sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\right)\mid}{\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\right)}} \\ $$$$\mathrm{R}.\mathrm{H}.\mathrm{L}.\:=\boldsymbol{\mathrm{e}}^{\mathrm{2}} \:\:;\:\:\:\mathrm{L}.\mathrm{H}.\mathrm{L}.\:=\boldsymbol{\mathrm{e}}^{−\mathrm{2}} \:=\frac{\mathrm{1}}{\boldsymbol{\mathrm{e}}^{\mathrm{2}} }\:. \\ $$$$\:\mathrm{so}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{dont}\:\mathrm{exist}\:\mathrm{at}\:\mathrm{x}=\pi\:. \\ $$
Commented by Joel577 last updated on 09/Aug/17

$$\mathrm{Can}\:\mathrm{u}\:\mathrm{explain}\:\mathrm{with}\:\mathrm{more}\:\mathrm{detail}\:\mathrm{Sir}? \\ $$$$\mathrm{I}\:\mathrm{dont}\:\mathrm{understand}\:\mathrm{from}\:\mathrm{the}\:\mathrm{second}\:\mathrm{row}\: \\ $$
Commented by ajfour last updated on 09/Aug/17
![since lim_(x→0) (1+x)^(1/x) =e here we have lim_(x→π) [1+sin^2 (π−x)]^(1/(sin^2 (π−x))) =e ..](Q19307.png)
$$\mathrm{since}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{1}/\mathrm{x}} =\mathrm{e} \\ $$$$\mathrm{here}\:\mathrm{we}\:\mathrm{have}\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\left[\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \left(\pi−\mathrm{x}\right)\right]^{\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \left(\pi−\mathrm{x}\right)}} =\mathrm{e} \\ $$$$.. \\ $$
