Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 19696 by Tinkutara last updated on 14/Aug/17

Let m be the smallest odd positive integer for which 1 + 2 + ... + m is a square of an integer and let n be the smallest even positive integer for which 1 + 2 + ... + n is a square of an integer. What is the value of m + n?

$$\mathrm{Let}\:{m}\:\mathrm{be}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{odd}\:\mathrm{positive} \\ $$$$\mathrm{integer}\:\mathrm{for}\:\mathrm{which}\:\mathrm{1}\:+\:\mathrm{2}\:+\:...\:+\:{m}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{square}\:\mathrm{of}\:\mathrm{an}\:\mathrm{integer}\:\mathrm{and}\:\mathrm{let}\:{n}\:\mathrm{be}\:\mathrm{the} \\ $$$$\mathrm{smallest}\:\mathrm{even}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{for} \\ $$$$\mathrm{which}\:\mathrm{1}\:+\:\mathrm{2}\:+\:...\:+\:{n}\:\mathrm{is}\:\mathrm{a}\:\mathrm{square}\:\mathrm{of}\:\mathrm{an} \\ $$$$\mathrm{integer}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{m}\:+\:{n}? \\ $$

Answered by Rasheed.Sindhi last updated on 15/Aug/17

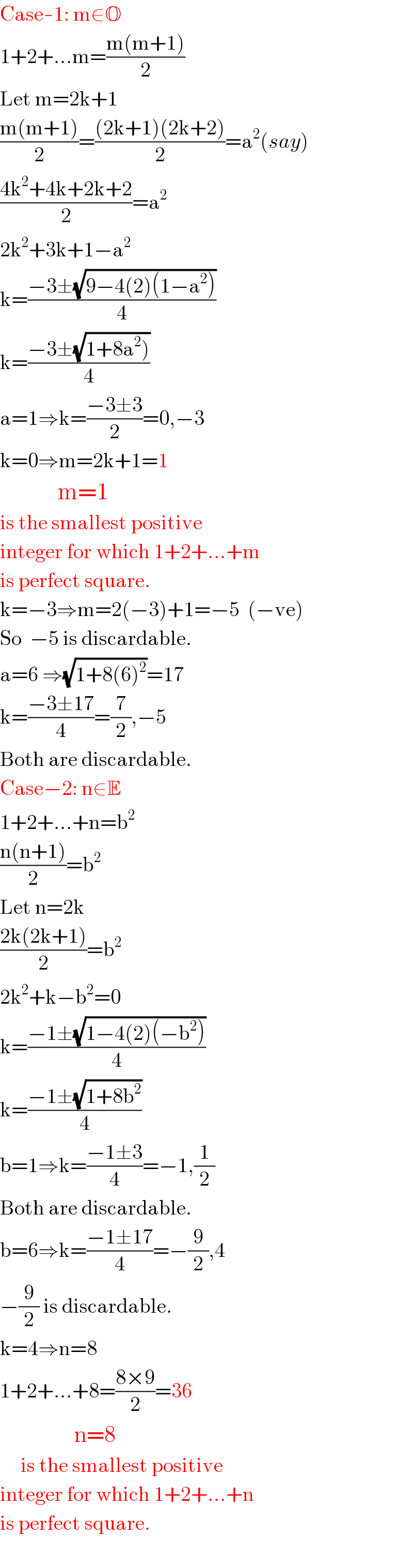
Case-1: m∈O 1+2+...m=((m(m+1))/2) Let m=2k+1 ((m(m+1))/2)=(((2k+1)(2k+2))/2)=a^2 (say) ((4k^2 +4k+2k+2)/2)=a^2 2k^2 +3k+1−a^2 k=((−3±(√(9−4(2)(1−a^2 ))))/4) k=((−3±(√(1+8a^2 ))))/4) a=1⇒k=((−3±3)/2)=0,−3 k=0⇒m=2k+1=1 m=1 is the smallest positive integer for which 1+2+...+m is perfect square. k=−3⇒m=2(−3)+1=−5 (−ve) So −5 is discardable. a=6 ⇒(√(1+8(6)^2 ))=17 k=((−3±17)/4)=(7/2),−5 Both are discardable. Case−2: n∈E 1+2+...+n=b^2 ((n(n+1))/2)=b^2 Let n=2k ((2k(2k+1))/2)=b^2 2k^2 +k−b^2 =0 k=((−1±(√(1−4(2)(−b^2 ))))/4) k=((−1±(√(1+8b^2 )))/4) b=1⇒k=((−1±3)/4)=−1,(1/2) Both are discardable. b=6⇒k=((−1±17)/4)=−(9/2),4 −(9/2) is discardable. k=4⇒n=8 1+2+...+8=((8×9)/2)=36 n=8 is the smallest positive integer for which 1+2+...+n is perfect square.

$$\mathrm{Case}-\mathrm{1}:\:\mathrm{m}\in\mathbb{O} \\ $$$$\mathrm{1}+\mathrm{2}+...\mathrm{m}=\frac{\mathrm{m}\left(\mathrm{m}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{Let}\:\mathrm{m}=\mathrm{2k}+\mathrm{1} \\ $$$$\frac{\mathrm{m}\left(\mathrm{m}+\mathrm{1}\right)}{\mathrm{2}}=\frac{\left(\mathrm{2k}+\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{2}\right)}{\mathrm{2}}=\mathrm{a}^{\mathrm{2}} \left({say}\right) \\ $$$$\frac{\mathrm{4k}^{\mathrm{2}} +\mathrm{4k}+\mathrm{2k}+\mathrm{2}}{\mathrm{2}}=\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{2k}^{\mathrm{2}} +\mathrm{3k}+\mathrm{1}−\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{k}=\frac{−\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{4}\left(\mathrm{2}\right)\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)}}{\mathrm{4}} \\ $$$$\mathrm{k}=\frac{−\mathrm{3}\pm\sqrt{\left.\mathrm{1}+\mathrm{8a}^{\mathrm{2}} \right)}}{\mathrm{4}} \\ $$$$\mathrm{a}=\mathrm{1}\Rightarrow\mathrm{k}=\frac{−\mathrm{3}\pm\mathrm{3}}{\mathrm{2}}=\mathrm{0},−\mathrm{3} \\ $$$$\mathrm{k}=\mathrm{0}\Rightarrow\mathrm{m}=\mathrm{2k}+\mathrm{1}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{m}=\mathrm{1} \\ $$$$\mathrm{is}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{positive} \\ $$$$\mathrm{integer}\:\mathrm{for}\:\mathrm{which}\:\mathrm{1}+\mathrm{2}+...+\mathrm{m} \\ $$$$\mathrm{is}\:\mathrm{perfect}\:\mathrm{square}. \\ $$$$\mathrm{k}=−\mathrm{3}\Rightarrow\mathrm{m}=\mathrm{2}\left(−\mathrm{3}\right)+\mathrm{1}=−\mathrm{5}\:\:\left(−\mathrm{ve}\right) \\ $$$$\mathrm{So}\:\:−\mathrm{5}\:\mathrm{is}\:\mathrm{discardable}. \\ $$$$\mathrm{a}=\mathrm{6}\:\Rightarrow\sqrt{\mathrm{1}+\mathrm{8}\left(\mathrm{6}\right)^{\mathrm{2}} }=\mathrm{17} \\ $$$$\mathrm{k}=\frac{−\mathrm{3}\pm\mathrm{17}}{\mathrm{4}}=\frac{\mathrm{7}}{\mathrm{2}},−\mathrm{5} \\ $$$$\mathrm{Both}\:\mathrm{are}\:\mathrm{discardable}. \\ $$$$\mathrm{Case}−\mathrm{2}:\:\mathrm{n}\in\mathbb{E} \\ $$$$\mathrm{1}+\mathrm{2}+...+\mathrm{n}=\mathrm{b}^{\mathrm{2}} \\ $$$$\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{b}^{\mathrm{2}} \\ $$$$\mathrm{Let}\:\mathrm{n}=\mathrm{2k} \\ $$$$\frac{\mathrm{2k}\left(\mathrm{2k}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{b}^{\mathrm{2}} \\ $$$$\mathrm{2k}^{\mathrm{2}} +\mathrm{k}−\mathrm{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{k}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}\left(\mathrm{2}\right)\left(−\mathrm{b}^{\mathrm{2}} \right)}}{\mathrm{4}} \\ $$$$\mathrm{k}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{8b}^{\mathrm{2}} }}{\mathrm{4}} \\ $$$$\mathrm{b}=\mathrm{1}\Rightarrow\mathrm{k}=\frac{−\mathrm{1}\pm\mathrm{3}}{\mathrm{4}}=−\mathrm{1},\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{Both}\:\mathrm{are}\:\mathrm{discardable}. \\ $$$$\mathrm{b}=\mathrm{6}\Rightarrow\mathrm{k}=\frac{−\mathrm{1}\pm\mathrm{17}}{\mathrm{4}}=−\frac{\mathrm{9}}{\mathrm{2}},\mathrm{4} \\ $$$$−\frac{\mathrm{9}}{\mathrm{2}}\:\mathrm{is}\:\mathrm{discardable}. \\ $$$$\mathrm{k}=\mathrm{4}\Rightarrow\mathrm{n}=\mathrm{8} \\ $$$$\mathrm{1}+\mathrm{2}+...+\mathrm{8}=\frac{\mathrm{8}×\mathrm{9}}{\mathrm{2}}=\mathrm{36} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{n}=\mathrm{8} \\ $$$$\:\:\:\:\:\mathrm{is}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{positive} \\ $$$$\mathrm{integer}\:\mathrm{for}\:\mathrm{which}\:\mathrm{1}+\mathrm{2}+...+\mathrm{n} \\ $$$$\mathrm{is}\:\mathrm{perfect}\:\mathrm{square}. \\ $$$$ \\ $$

Commented by Tinkutara last updated on 15/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com