Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 20550 by Tinkutara last updated on 28/Aug/17

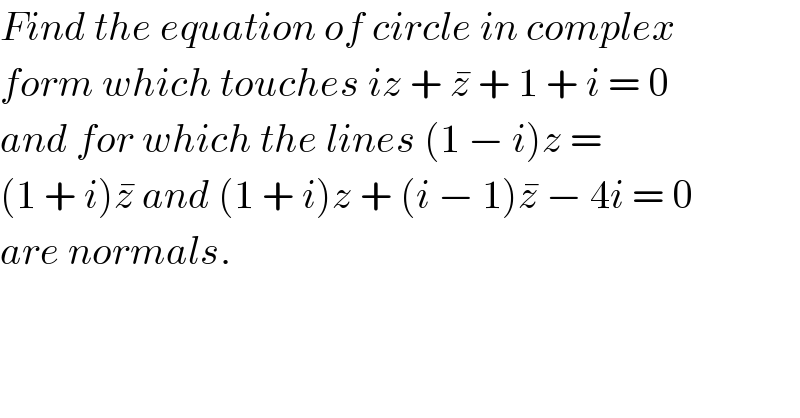
Find the equation of circle in complex form which touches iz + z^� + 1 + i = 0 and for which the lines (1 − i)z = (1 + i)z^� and (1 + i)z + (i − 1)z^� − 4i = 0 are normals.

$${Find}\:{the}\:{equation}\:{of}\:{circle}\:{in}\:{complex} \\ $$$${form}\:{which}\:{touches}\:{iz}\:+\:\bar {{z}}\:+\:\mathrm{1}\:+\:{i}\:=\:\mathrm{0} \\ $$$${and}\:{for}\:{which}\:{the}\:{lines}\:\left(\mathrm{1}\:−\:{i}\right){z}\:= \\ $$$$\left(\mathrm{1}\:+\:{i}\right)\bar {{z}}\:{and}\:\left(\mathrm{1}\:+\:{i}\right){z}\:+\:\left({i}\:−\:\mathrm{1}\right)\bar {{z}}\:−\:\mathrm{4}{i}\:=\:\mathrm{0} \\ $$$${are}\:{normals}. \\ $$

Answered by ajfour last updated on 30/Aug/17

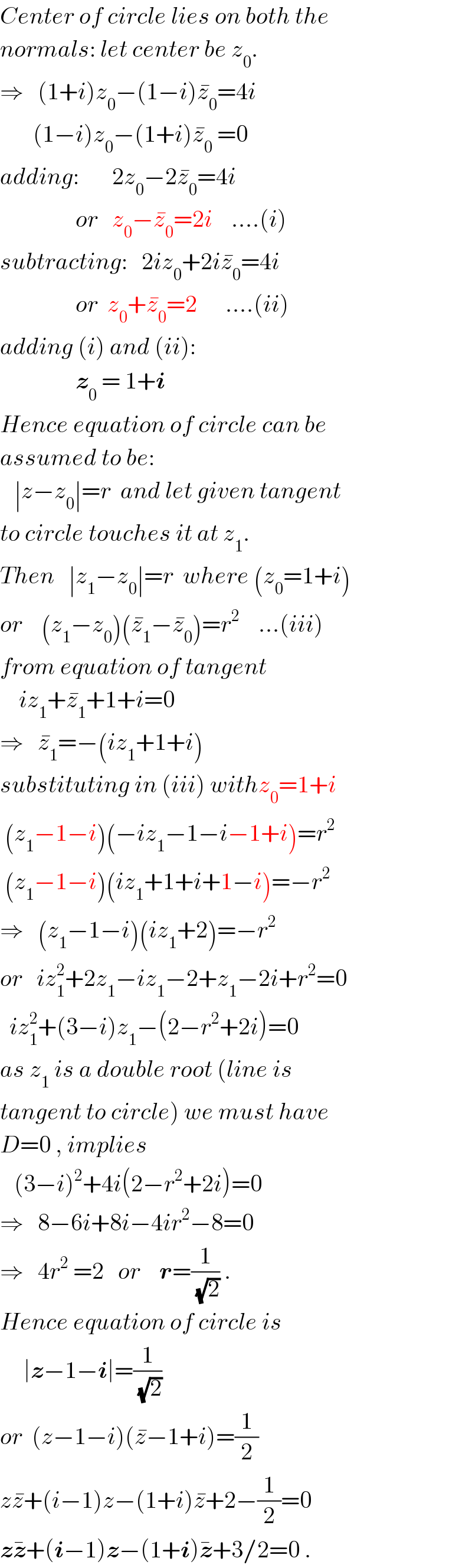
Center of circle lies on both the normals: let center be z_0 . ⇒ (1+i)z_0 −(1−i)z_0 ^� =4i (1−i)z_0 −(1+i)z_0 ^� =0 adding: 2z_0 −2z_0 ^� =4i or z_0 −z_0 ^� =2i ....(i) subtracting: 2iz_0 +2iz_0 ^� =4i or z_0 +z_0 ^� =2 ....(ii) adding (i) and (ii): z_0 = 1+i Hence equation of circle can be assumed to be: ∣z−z_0 ∣=r and let given tangent to circle touches it at z_1 . Then ∣z_1 −z_0 ∣=r where (z_0 =1+i) or (z_1 −z_0 )(z_1 ^� −z_0 ^� )=r^2 ...(iii) from equation of tangent iz_1 +z_1 ^� +1+i=0 ⇒ z_1 ^� =−(iz_1 +1+i) substituting in (iii) withz_0 =1+i (z_1 −1−i)(−iz_1 −1−i−1+i)=r^2 (z_1 −1−i)(iz_1 +1+i+1−i)=−r^2 ⇒ (z_1 −1−i)(iz_1 +2)=−r^2 or iz_1 ^2 +2z_1 −iz_1 −2+z_1 −2i+r^2 =0 iz_1 ^2 +(3−i)z_1 −(2−r^2 +2i)=0 as z_1 is a double root (line is tangent to circle) we must have D=0 , implies (3−i)^2 +4i(2−r^2 +2i)=0 ⇒ 8−6i+8i−4ir^2 −8=0 ⇒ 4r^2 =2 or r=(1/(√2)) . Hence equation of circle is ∣z−1−i∣=(1/(√2)) or (z−1−i)(z^� −1+i)=(1/2) zz^� +(i−1)z−(1+i)z^� +2−(1/2)=0 zz^� +(i−1)z−(1+i)z^� +3/2=0 .

$${Center}\:{of}\:{circle}\:{lies}\:{on}\:{both}\:{the}\: \\ $$$${normals}:\:{let}\:{center}\:{be}\:{z}_{\mathrm{0}} . \\ $$$$\Rightarrow\:\:\:\left(\mathrm{1}+{i}\right){z}_{\mathrm{0}} −\left(\mathrm{1}−{i}\right)\bar {{z}}_{\mathrm{0}} =\mathrm{4}{i} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{1}−{i}\right){z}_{\mathrm{0}} −\left(\mathrm{1}+{i}\right)\bar {{z}}_{\mathrm{0}} \:=\mathrm{0} \\ $$$${adding}:\:\:\:\:\:\:\:\mathrm{2}{z}_{\mathrm{0}} −\mathrm{2}\bar {{z}}_{\mathrm{0}} =\mathrm{4}{i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{or}\:\:\:{z}_{\mathrm{0}} −\bar {{z}}_{\mathrm{0}} =\mathrm{2}{i}\:\:\:\:....\left({i}\right) \\ $$$${subtracting}:\:\:\:\mathrm{2}{iz}_{\mathrm{0}} +\mathrm{2}{i}\bar {{z}}_{\mathrm{0}} =\mathrm{4}{i} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{or}\:\:{z}_{\mathrm{0}} +\bar {{z}}_{\mathrm{0}} =\mathrm{2}\:\:\:\:\:\:....\left({ii}\right) \\ $$$${adding}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{z}}_{\mathrm{0}} \:=\:\mathrm{1}+\boldsymbol{{i}} \\ $$$${Hence}\:{equation}\:{of}\:{circle}\:{can}\:{be} \\ $$$${assumed}\:{to}\:{be}: \\ $$$$\:\:\:\mid{z}−{z}_{\mathrm{0}} \mid={r}\:\:{and}\:{let}\:{given}\:{tangent} \\ $$$${to}\:{circle}\:{touches}\:{it}\:{at}\:{z}_{\mathrm{1}} . \\ $$$${Then}\:\:\:\mid{z}_{\mathrm{1}} −{z}_{\mathrm{0}} \mid={r}\:\:{where}\:\left({z}_{\mathrm{0}} =\mathrm{1}+{i}\right) \\ $$$${or}\:\:\:\:\left({z}_{\mathrm{1}} −{z}_{\mathrm{0}} \right)\left(\bar {{z}}_{\mathrm{1}} −\bar {{z}}_{\mathrm{0}} \right)={r}^{\mathrm{2}} \:\:\:\:...\left({iii}\right) \\ $$$${from}\:{equation}\:{of}\:{tangent} \\ $$$$\:\:\:\:{iz}_{\mathrm{1}} +\bar {{z}}_{\mathrm{1}} +\mathrm{1}+{i}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\bar {{z}}_{\mathrm{1}} =−\left({iz}_{\mathrm{1}} +\mathrm{1}+{i}\right) \\ $$$${substituting}\:{in}\:\left({iii}\right)\:{withz}_{\mathrm{0}} =\mathrm{1}+{i} \\ $$$$\:\left({z}_{\mathrm{1}} −\mathrm{1}−{i}\right)\left(−{iz}_{\mathrm{1}} −\mathrm{1}−{i}−\mathrm{1}+{i}\right)={r}^{\mathrm{2}} \\ $$$$\:\left({z}_{\mathrm{1}} −\mathrm{1}−{i}\right)\left({iz}_{\mathrm{1}} +\mathrm{1}+{i}+\mathrm{1}−{i}\right)=−{r}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\left({z}_{\mathrm{1}} −\mathrm{1}−{i}\right)\left({iz}_{\mathrm{1}} +\mathrm{2}\right)=−{r}^{\mathrm{2}} \\ $$$${or}\:\:\:{iz}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}{z}_{\mathrm{1}} −{iz}_{\mathrm{1}} −\mathrm{2}+{z}_{\mathrm{1}} −\mathrm{2}{i}+{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:{iz}_{\mathrm{1}} ^{\mathrm{2}} +\left(\mathrm{3}−{i}\right){z}_{\mathrm{1}} −\left(\mathrm{2}−{r}^{\mathrm{2}} +\mathrm{2}{i}\right)=\mathrm{0} \\ $$$${as}\:{z}_{\mathrm{1}} \:{is}\:{a}\:{double}\:{root}\:\left({line}\:{is}\right. \\ $$$$\left.{tangent}\:{to}\:{circle}\right)\:{we}\:{must}\:{have} \\ $$$${D}=\mathrm{0}\:,\:{implies} \\ $$$$\:\:\:\left(\mathrm{3}−{i}\right)^{\mathrm{2}} +\mathrm{4}{i}\left(\mathrm{2}−{r}^{\mathrm{2}} +\mathrm{2}{i}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{8}−\mathrm{6}{i}+\mathrm{8}{i}−\mathrm{4}{ir}^{\mathrm{2}} −\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{4}{r}^{\mathrm{2}} \:=\mathrm{2}\:\:\:{or}\:\:\:\:\boldsymbol{{r}}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:. \\ $$$${Hence}\:{equation}\:{of}\:{circle}\:{is} \\ $$$$\:\:\:\:\:\mid\boldsymbol{{z}}−\mathrm{1}−\boldsymbol{{i}}\mid=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$${or}\:\:\left({z}−\mathrm{1}−{i}\right)\left(\bar {{z}}−\mathrm{1}+{i}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${z}\bar {{z}}+\left({i}−\mathrm{1}\right){z}−\left(\mathrm{1}+{i}\right)\bar {{z}}+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\boldsymbol{{z}}\bar {\boldsymbol{{z}}}+\left(\boldsymbol{{i}}−\mathrm{1}\right)\boldsymbol{{z}}−\left(\mathrm{1}+\boldsymbol{{i}}\right)\bar {\boldsymbol{{z}}}+\mathrm{3}/\mathrm{2}=\mathrm{0}\:. \\ $$

Commented by Tinkutara last updated on 30/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com