
Question Number 20785 by Tinkutara last updated on 02/Sep/17
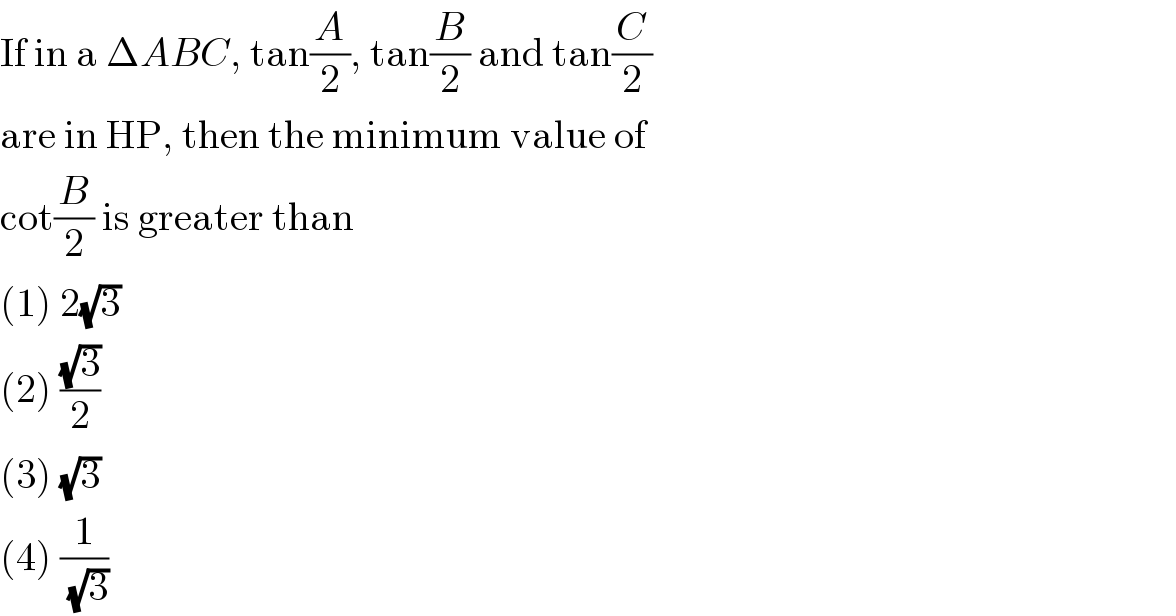
$$\mathrm{If}\:\mathrm{in}\:\mathrm{a}\:\Delta{ABC},\:\mathrm{tan}\frac{{A}}{\mathrm{2}},\:\mathrm{tan}\frac{{B}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{tan}\frac{{C}}{\mathrm{2}} \\ $$$$\mathrm{are}\:\mathrm{in}\:\mathrm{HP},\:\mathrm{then}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{cot}\frac{{B}}{\mathrm{2}}\:\mathrm{is}\:\mathrm{greater}\:\mathrm{than} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:\sqrt{\mathrm{3}} \\ $$$$\left(\mathrm{4}\right)\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$
Answered by ajfour last updated on 03/Sep/17
![let us call tan (A/2)=x, tan (B/2)=y, tan (C/2)=z . given x, y, z are in H.P. ⇒ y=((2xz)/(x+z)) ......(i) tan ((A/2)+(B/2)+(C/2))=((Σtan (A/2)−Πtan (A/2))/(1−Σtan (A/2)tan (B/2))) ⇒ 1−Σxy=0 or y(x+z)+xz=1 y=((1−xz)/(x+z)) ......(ii) from (i) and (ii) it follows that 2xz=1−xz ⇒ xz=(1/3) we know that A.M. ≥ G.M. (((x+z)/2))^2 ≥ xz ......(iii) y= ((2xz)/(x+z)) [eq.(i)] and xz=1/3 ⇒ x+z=(2/(3y)) ; using this in (iii) ((1/(3y)))^2 ≥(1/3) ⇒ (1/y) ≥ (√3) ⇒ cot (B/2) ≥ (√3) .](Q20794.png)
$${let}\:{us}\:{call}\:\:\:\:\mathrm{tan}\:\frac{{A}}{\mathrm{2}}={x},\:\mathrm{tan}\:\frac{{B}}{\mathrm{2}}={y}, \\ $$$$\mathrm{tan}\:\frac{{C}}{\mathrm{2}}={z}\:. \\ $$$$\:\:\:\:{given}\:{x},\:{y},\:{z}\:{are}\:{in}\:{H}.{P}. \\ $$$$\Rightarrow\:\:\:{y}=\frac{\mathrm{2}{xz}}{{x}+{z}}\:\:\:\:......\left({i}\right) \\ $$$$\:\:\:\mathrm{tan}\:\left(\frac{{A}}{\mathrm{2}}+\frac{{B}}{\mathrm{2}}+\frac{{C}}{\mathrm{2}}\right)=\frac{\Sigma\mathrm{tan}\:\frac{{A}}{\mathrm{2}}−\Pi\mathrm{tan}\:\frac{{A}}{\mathrm{2}}}{\mathrm{1}−\Sigma\mathrm{tan}\:\frac{{A}}{\mathrm{2}}\mathrm{tan}\:\frac{{B}}{\mathrm{2}}} \\ $$$$\Rightarrow\:\:\:\mathrm{1}−\Sigma{xy}=\mathrm{0} \\ $$$${or}\:\:\:\:{y}\left({x}+{z}\right)+{xz}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}=\frac{\mathrm{1}−{xz}}{{x}+{z}}\:\:\:\:\:......\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{it}\:{follows}\:{that} \\ $$$$\:\:\:\:\:\mathrm{2}{xz}=\mathrm{1}−{xz}\:\:\:\:\:\Rightarrow\:\:\:\:{xz}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:\:\:\:{we}\:{know}\:{that}\:{A}.{M}.\:\geqslant\:{G}.{M}. \\ $$$$\:\:\:\:\:\left(\frac{{x}+{z}}{\mathrm{2}}\right)^{\mathrm{2}} \:\geqslant\:{xz}\:\:\:......\left({iii}\right) \\ $$$$\:\:\:{y}=\:\frac{\mathrm{2}{xz}}{{x}+{z}}\:\:\:\:\:\left[{eq}.\left({i}\right)\right]\:\:{and}\:{xz}=\mathrm{1}/\mathrm{3} \\ $$$$\Rightarrow\:\:{x}+{z}=\frac{\mathrm{2}}{\mathrm{3}{y}}\:;\:{using}\:{this}\:{in}\:\left({iii}\right) \\ $$$$\:\:\:\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{3}{y}}\right)^{\mathrm{2}} \:\geqslant\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\Rightarrow\:\:\:\frac{\mathrm{1}}{{y}}\:\geqslant\:\sqrt{\mathrm{3}}\: \\ $$$$\Rightarrow\:\:\:\:\mathrm{cot}\:\frac{{B}}{\mathrm{2}}\:\geqslant\:\sqrt{\mathrm{3}}\:. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 03/Sep/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
