Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 21357 by Tinkutara last updated on 21/Sep/17

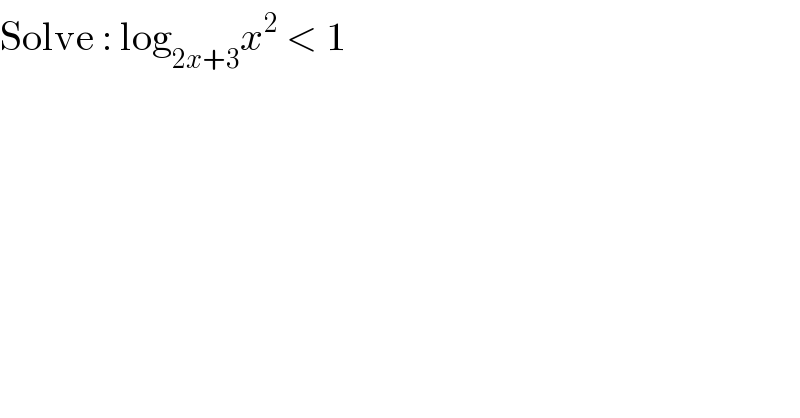
Solve : log_(2x+3) x^2 < 1

$$\mathrm{Solve}\::\:\mathrm{log}_{\mathrm{2}{x}+\mathrm{3}} {x}^{\mathrm{2}} \:<\:\mathrm{1} \\ $$

Answered by dioph last updated on 21/Sep/17

2x + 3 > 0 ⇒ x > −(3/2) 2x + 3 ≠ 1 ⇒ x ≠ −1 ((log x^2 )/(log 2x+3)) < 1 Case 1: x < −1 (2x + 3 < 1) log 2x + 3 < 0 ⇒ log x^2 > log 2x+3 ⇒ log (x^2 /(2x+3)) > 0 ⇒ (x^2 /(2x+3)) > 1 ⇒ x^2 −2x − 3 > 0 ⇒ x ∈ (−∞,−1) ∪ (3, +∞) but x < −1 ⇒ x ∈ (−∞,−1) Case 2: x > −1 (2x+3 > 1) log 2x+3 > 0 ⇒ log x^2 < log 2x+3 ⇒ log (x^2 /(2x+3)) < 0 ⇒ (x^2 /(2x+3)) < 1 ⇒ x^2 −2x−3 < 0 ⇒ x ∈ (−1,3) x > −1 ⇒ x ∈ (−1, 3) putting together: x ∈ (−(3/2), 3) − {−1}

$$\mathrm{2}{x}\:+\:\mathrm{3}\:>\:\mathrm{0}\:\Rightarrow\:{x}\:>\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$ $$\mathrm{2}{x}\:+\:\mathrm{3}\:\neq\:\mathrm{1}\:\Rightarrow\:{x}\:\neq\:−\mathrm{1} \\ $$ $$\frac{\mathrm{log}\:{x}^{\mathrm{2}} }{\mathrm{log}\:\mathrm{2}{x}+\mathrm{3}}\:<\:\mathrm{1} \\ $$ $$\mathrm{Case}\:\mathrm{1}:\:{x}\:<\:−\mathrm{1}\:\left(\mathrm{2}{x}\:+\:\mathrm{3}\:<\:\mathrm{1}\right) \\ $$ $$\mathrm{log}\:\mathrm{2}{x}\:+\:\mathrm{3}\:<\:\mathrm{0} \\ $$ $$\Rightarrow\:\mathrm{log}\:{x}^{\mathrm{2}} \:>\:\mathrm{log}\:\mathrm{2}{x}+\mathrm{3} \\ $$ $$\Rightarrow\:\mathrm{log}\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}+\mathrm{3}}\:>\:\mathrm{0} \\ $$ $$\Rightarrow\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}+\mathrm{3}}\:>\:\mathrm{1} \\ $$ $$\Rightarrow\:{x}^{\mathrm{2}} \:\:−\mathrm{2}{x}\:−\:\mathrm{3}\:>\:\mathrm{0} \\ $$ $$\Rightarrow\:{x}\:\in\:\left(−\infty,−\mathrm{1}\right)\:\cup\:\left(\mathrm{3},\:+\infty\right) \\ $$ $$\mathrm{but}\:{x}\:<\:−\mathrm{1}\:\Rightarrow\:{x}\:\in\:\left(−\infty,−\mathrm{1}\right) \\ $$ $$\mathrm{Case}\:\mathrm{2}:\:{x}\:>\:−\mathrm{1}\:\left(\mathrm{2}{x}+\mathrm{3}\:>\:\mathrm{1}\right) \\ $$ $$\mathrm{log}\:\mathrm{2}{x}+\mathrm{3}\:>\:\mathrm{0} \\ $$ $$\Rightarrow\:\mathrm{log}\:{x}^{\mathrm{2}} \:<\:\mathrm{log}\:\mathrm{2}{x}+\mathrm{3} \\ $$ $$\Rightarrow\:\mathrm{log}\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}+\mathrm{3}}\:<\:\mathrm{0} \\ $$ $$\Rightarrow\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}+\mathrm{3}}\:<\:\mathrm{1} \\ $$ $$\Rightarrow\:{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}\:<\:\mathrm{0} \\ $$ $$\Rightarrow\:{x}\:\in\:\left(−\mathrm{1},\mathrm{3}\right) \\ $$ $${x}\:>\:−\mathrm{1}\:\Rightarrow\:{x}\:\in\:\left(−\mathrm{1},\:\mathrm{3}\right) \\ $$ $$\mathrm{putting}\:\mathrm{together}: \\ $$ $${x}\:\in\:\left(−\frac{\mathrm{3}}{\mathrm{2}},\:\mathrm{3}\right)\:−\:\left\{−\mathrm{1}\right\} \\ $$

Commented byTinkutara last updated on 21/Sep/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com