Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 21519 by ram1234 last updated on 26/Sep/17

If th roots of the equation x^2 +2ax+b=0 are real and disinct and they differ by at most 2m, then b lies in the interval

$$\mathrm{If}\:\mathrm{th}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:{x}^{\mathrm{2}} +\mathrm{2}{ax}+{b}=\mathrm{0} \\ $$$$\mathrm{are}\:\mathrm{real}\:\mathrm{and}\:\mathrm{disinct}\:\mathrm{and}\:\mathrm{they}\:\mathrm{differ}\:\mathrm{by} \\ $$$$\mathrm{at}\:\mathrm{most}\:\mathrm{2}{m},\:\mathrm{then}\:\:{b}\:\mathrm{lies}\:\mathrm{in}\:\mathrm{the}\:\mathrm{interval} \\ $$

Answered by mrW1 last updated on 26/Sep/17

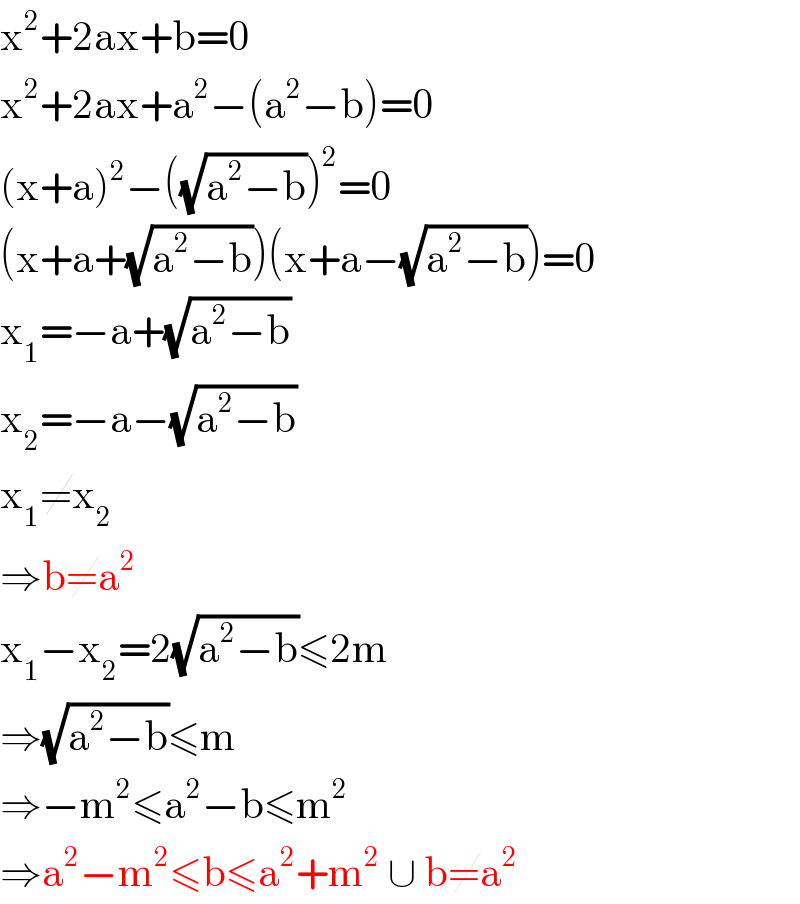
x^2 +2ax+b=0 x^2 +2ax+a^2 −(a^2 −b)=0 (x+a)^2 −((√(a^2 −b)))^2 =0 (x+a+(√(a^2 −b)))(x+a−(√(a^2 −b)))=0 x_1 =−a+(√(a^2 −b)) x_2 =−a−(√(a^2 −b)) x_1 ≠x_2 ⇒b≠a^2 x_1 −x_2 =2(√(a^2 −b))≤2m ⇒(√(a^2 −b))≤m ⇒−m^2 ≤a^2 −b≤m^2 ⇒a^2 −m^2 ≤b≤a^2 +m^2 ∪ b≠a^2

$$\mathrm{x}^{\mathrm{2}} +\mathrm{2ax}+\mathrm{b}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{2ax}+\mathrm{a}^{\mathrm{2}} −\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}\right)=\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{a}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}}\right)\left(\mathrm{x}+\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}}\right)=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1}} =−\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}} \\ $$$$\mathrm{x}_{\mathrm{2}} =−\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}} \\ $$$$\mathrm{x}_{\mathrm{1}} \neq\mathrm{x}_{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{b}\neq\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{x}_{\mathrm{1}} −\mathrm{x}_{\mathrm{2}} =\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}}\leqslant\mathrm{2m} \\ $$$$\Rightarrow\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}}\leqslant\mathrm{m} \\ $$$$\Rightarrow−\mathrm{m}^{\mathrm{2}} \leqslant\mathrm{a}^{\mathrm{2}} −\mathrm{b}\leqslant\mathrm{m}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} −\mathrm{m}^{\mathrm{2}} \leqslant\mathrm{b}\leqslant\mathrm{a}^{\mathrm{2}} +\mathrm{m}^{\mathrm{2}} \:\cup\:\mathrm{b}\neq\mathrm{a}^{\mathrm{2}} \\ $$

Commented by Joel577 last updated on 26/Sep/17

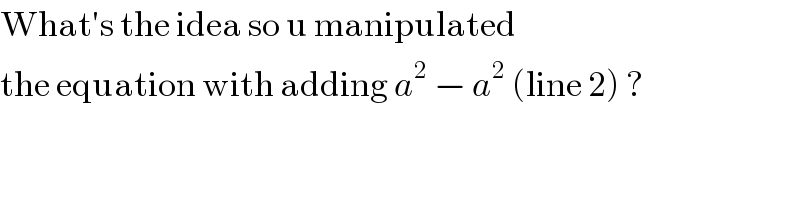
What′s the idea so u manipulated the equation with adding a^2 − a^2 (line 2) ?

$$\mathrm{What}'\mathrm{s}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{so}\:\mathrm{u}\:\mathrm{manipulated} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{with}\:\mathrm{adding}\:{a}^{\mathrm{2}} \:−\:{a}^{\mathrm{2}} \:\left(\mathrm{line}\:\mathrm{2}\right)\:? \\ $$

Commented by mrW1 last updated on 26/Sep/17

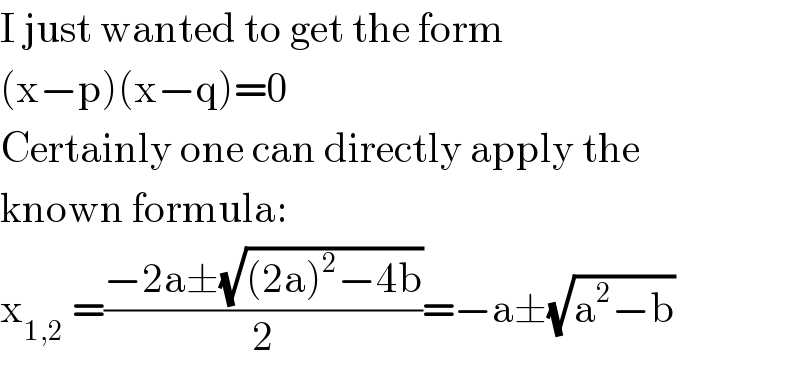
I just wanted to get the form (x−p)(x−q)=0 Certainly one can directly apply the known formula: x_(1,2) =((−2a±(√((2a)^2 −4b)))/2)=−a±(√(a^2 −b))

$$\mathrm{I}\:\mathrm{just}\:\mathrm{wanted}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{form} \\ $$$$\left(\mathrm{x}−\mathrm{p}\right)\left(\mathrm{x}−\mathrm{q}\right)=\mathrm{0} \\ $$$$\mathrm{Certainly}\:\mathrm{one}\:\mathrm{can}\:\mathrm{directly}\:\mathrm{apply}\:\mathrm{the} \\ $$$$\mathrm{known}\:\mathrm{formula}: \\ $$$$\mathrm{x}_{\mathrm{1},\mathrm{2}} \:=\frac{−\mathrm{2a}\pm\sqrt{\left(\mathrm{2a}\right)^{\mathrm{2}} −\mathrm{4b}}}{\mathrm{2}}=−\mathrm{a}\pm\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com