Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 2478 by Syaka last updated on 21/Nov/15

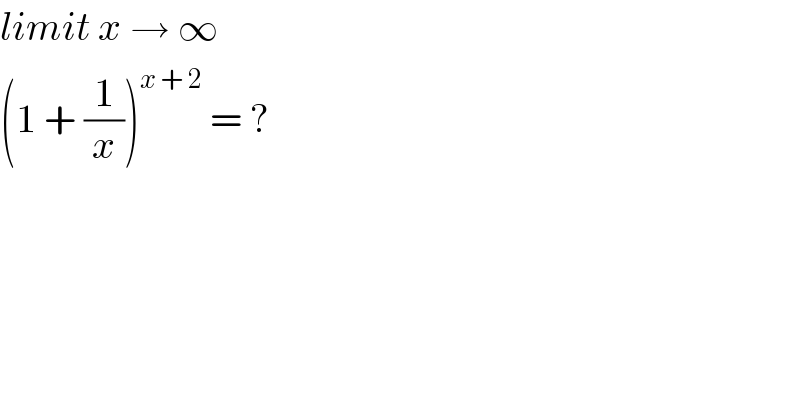
limit x → ∞ (1 + (1/x))^(x + 2) = ?

$${limit}\:{x}\:\rightarrow\:\infty \\ $$$$\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{x}}\right)^{{x}\:+\:\mathrm{2}} \:=\:? \\ $$

Commented by John_Haha last updated on 21/Nov/15

e

$${e} \\ $$

Answered by Yozzi last updated on 21/Nov/15

L=lim_(x→∞) (1+(1/x))^(x+2) =lim_(x→∞) (1+(1/x))^2 (1+(1/x))^x L=(lim_(x→∞) (1+(1/x))^2 )(lim_(x→∞) (1+(1/x))^x ) L=((1+(1/∞))^2 )(e) L=1^2 ×e=e Proof for lim_(x→∞) (1+1/x)^x =e Let l=lim_(x→∞) (1+1/x)^x (∗). (1+1/x)^x >0 ∀x>0 so if l exists, l>0. Taking logs to base e on both sides of (∗). lnl=lim_(x→∞) ln(1+1/x)^x lnl=lim_(x→∞) xln(1+(1/x)) Let u=1/x⇒as x→∞,u→0. ∴lnl=lim_(u→0) (1/u)ln(1+u) Using the Maclaurin expansion for ln(1+u)=u−(u^2 /2)+(u^3 /3)−(u^4 /4)+(u^5 /5)−... −1<u≤1 ⇒lnl=lim_(u→0) (1/u)(u−(u^2 /2)+(u^3 /3)−(u^4 /4)+(u^5 /5)−...) lnl=lim_(u→0) (1−(u/2)+(u^2 /3)−(u^3 /4)+(u^4 /5)−...) lnl=1−0+0−0+0−... lnl=1⇒l=e ∴ lim_(x→∞) (1+(1/x))^x =e

$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}+\mathrm{2}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} \\ $$$${L}=\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \right)\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} \right) \\ $$$${L}=\left(\left(\mathrm{1}+\frac{\mathrm{1}}{\infty}\right)^{\mathrm{2}} \right)\left({e}\right) \\ $$$${L}=\mathrm{1}^{\mathrm{2}} ×{e}={e} \\ $$$$ \\ $$$${Proof}\:{for}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{1}/{x}\right)^{{x}} ={e} \\ $$$${Let}\:{l}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{1}/{x}\right)^{{x}} \:\:\left(\ast\right). \\ $$$$\left(\mathrm{1}+\mathrm{1}/{x}\right)^{{x}} >\mathrm{0}\:\forall{x}>\mathrm{0}\:{so}\:{if}\:{l}\:{exists},\:{l}>\mathrm{0}. \\ $$$${Taking}\:{logs}\:{to}\:{base}\:{e}\:{on}\:{both}\:{sides}\:{of}\:\left(\ast\right). \\ $$$${lnl}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{ln}\left(\mathrm{1}+\mathrm{1}/{x}\right)^{{x}} \\ $$$${lnl}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}{xln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${Let}\:{u}=\mathrm{1}/{x}\Rightarrow{as}\:{x}\rightarrow\infty,{u}\rightarrow\mathrm{0}. \\ $$$$\therefore{lnl}=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{u}}{ln}\left(\mathrm{1}+{u}\right) \\ $$$${Using}\:{the}\:{Maclaurin}\:{expansion}\:{for} \\ $$$${ln}\left(\mathrm{1}+{u}\right)={u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+\frac{{u}^{\mathrm{3}} }{\mathrm{3}}−\frac{{u}^{\mathrm{4}} }{\mathrm{4}}+\frac{{u}^{\mathrm{5}} }{\mathrm{5}}−...\:\:\:−\mathrm{1}<{u}\leqslant\mathrm{1} \\ $$$$\Rightarrow{lnl}=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{u}}\left({u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+\frac{{u}^{\mathrm{3}} }{\mathrm{3}}−\frac{{u}^{\mathrm{4}} }{\mathrm{4}}+\frac{{u}^{\mathrm{5}} }{\mathrm{5}}−...\right) \\ $$$${lnl}=\underset{{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}−\frac{{u}}{\mathrm{2}}+\frac{{u}^{\mathrm{2}} }{\mathrm{3}}−\frac{{u}^{\mathrm{3}} }{\mathrm{4}}+\frac{{u}^{\mathrm{4}} }{\mathrm{5}}−...\right) \\ $$$${lnl}=\mathrm{1}−\mathrm{0}+\mathrm{0}−\mathrm{0}+\mathrm{0}−... \\ $$$${lnl}=\mathrm{1}\Rightarrow{l}={e} \\ $$$$\therefore\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}} ={e} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com