Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 264 by novrya last updated on 17/Dec/14

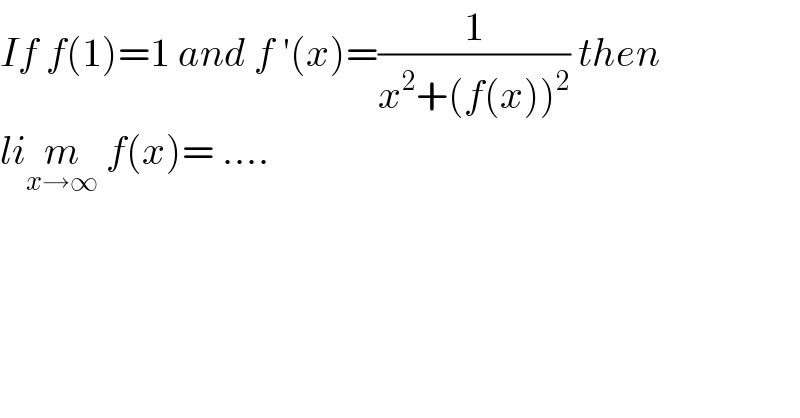
If f(1)=1 and f ′(x)=(1/(x^2 +(f(x))^2 )) then lim_(x→∞) f(x)= ....

$${If}\:{f}\left(\mathrm{1}\right)=\mathrm{1}\:{and}\:{f}\:'\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:{then}\: \\ $$$${li}\underset{{x}\rightarrow\infty} {{m}}\:{f}\left({x}\right)=\:.... \\ $$

Commented by 123456 last updated on 17/Dec/14

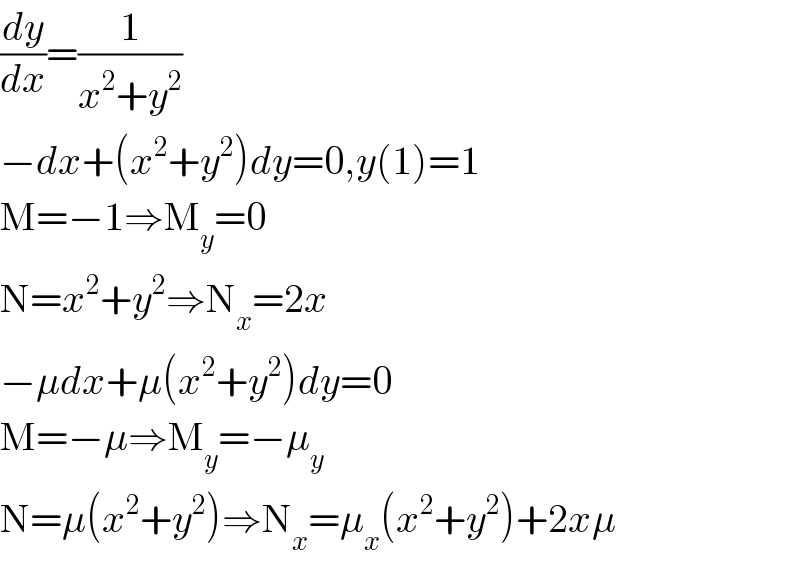
(dy/dx)=(1/(x^2 +y^2 )) −dx+(x^2 +y^2 )dy=0,y(1)=1 M=−1⇒M_y =0 N=x^2 +y^2 ⇒N_x =2x −μdx+μ(x^2 +y^2 )dy=0 M=−μ⇒M_y =−μ_y N=μ(x^2 +y^2 )⇒N_x =μ_x (x^2 +y^2 )+2xμ

$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$−{dx}+\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dy}=\mathrm{0},{y}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{M}=−\mathrm{1}\Rightarrow\mathrm{M}_{{y}} =\mathrm{0} \\ $$$$\mathrm{N}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \Rightarrow\mathrm{N}_{{x}} =\mathrm{2}{x} \\ $$$$−\mu{dx}+\mu\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dy}=\mathrm{0} \\ $$$$\mathrm{M}=−\mu\Rightarrow\mathrm{M}_{{y}} =−\mu_{{y}} \\ $$$$\mathrm{N}=\mu\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\Rightarrow\mathrm{N}_{{x}} =\mu_{{x}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)+\mathrm{2}{x}\mu \\ $$

Commented by 123456 last updated on 21/Dec/14

the equation is hard and its possible that cannot be doing using elementary functions... i thinks thats exist other ways to compute it...

$$\mathrm{the}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{hard}\:\mathrm{and}\:\mathrm{its}\:\mathrm{possible}\:\mathrm{that}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{doing}\:\mathrm{using}\:\mathrm{elementary}\:\mathrm{functions}... \\ $$$$\mathrm{i}\:\mathrm{thinks}\:\mathrm{thats}\:\:\mathrm{exist}\:\mathrm{other}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{compute}\:\mathrm{it}... \\ $$

Commented by 123456 last updated on 17/Feb/15

∫_1 ^x f′(t)dt=∫_1 ^x (dt/(t^2 +[f(t)]^2 ))≤∫_1 ^x (dt/(t^2 +1)) f(x)−1≤(π/2)−(π/4)=(π/4) f(x)≤1+(π/4) f′=(1/(x^2 +f^2 ))>0,x≥1 (1/(x^2 +f^2 ))→0,x→+∞

$$\underset{\mathrm{1}} {\overset{{x}} {\int}}{f}'\left({t}\right){dt}=\underset{\mathrm{1}} {\overset{{x}} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +\left[{f}\left({t}\right)\right]^{\mathrm{2}} }\leqslant\underset{\mathrm{1}} {\overset{{x}} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${f}\left({x}\right)−\mathrm{1}\leqslant\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}} \\ $$$${f}\left({x}\right)\leqslant\mathrm{1}+\frac{\pi}{\mathrm{4}} \\ $$$${f}'=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{f}^{\mathrm{2}} }>\mathrm{0},{x}\geqslant\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{f}^{\mathrm{2}} }\rightarrow\mathrm{0},{x}\rightarrow+\infty \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com