
Question Number 26558 by abdo imad last updated on 26/Dec/17
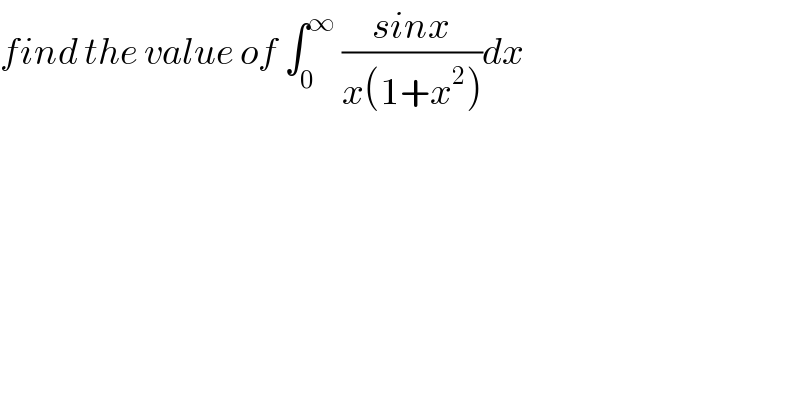
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$
Commented by abdo imad last updated on 27/Dec/17
![let put I= ∫_0 ^∞ ((sinx)/(x(1+x^2 ))) dx we know that ∫_0 ^∞ ((cos(αx))/(1+x^2 )) dx= (π/2) e^(−α) let take α≥0⇒ ∫_0 ^1 (π/2) e^(−α) dα= −(π/2)[ e^(−α) ]_0 ^1 =−(π/2)( e^(−1) −1) =(π/2)(1− e^(−1) ) and from another side ∫_0 ^1 (π/2) e^(−α) dα = ∫_0 ^1 (∫_0 ^∞ ((cos(αx))/(1+x^2 ))dx)dα = ∫_0 ^∞ ( ∫_0 ^1 cos(αx)dα)(dx/(1+x^2 )) (by fubini theorem ) =∫_0 ^∞ ( [((sin(αx))/x) ]_(α=0) ^(α=1) ) (dx/(1+x^2 ))= ∫_0 ^∞ ((sinx)/x).(( dx)/(1+x^2 )) ⇒ ∫_0 ^∞ ((sinx)/(x(1+x^2 )))dx= (π/2)(1− (1/e)).](Q26616.png)
$${let}\:{put}\:\:{I}=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{dx}\:\:\:{we}\:{know}\:{that}\:\:\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left(\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}=\:\frac{\pi}{\mathrm{2}}\:{e}^{−\alpha} \\ $$$${let}\:{take}\:\alpha\geqslant\mathrm{0}\Rightarrow\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\pi}{\mathrm{2}}\:{e}^{−\alpha} {d}\alpha=\:−\frac{\pi}{\mathrm{2}}\left[\:{e}^{−\alpha} \right]_{\mathrm{0}} ^{\mathrm{1}} =−\frac{\pi}{\mathrm{2}}\left(\:{e}^{−\mathrm{1}} −\mathrm{1}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\:{e}^{−\mathrm{1}} \right)\:{and}\:{from}\:{another}\:{side} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\pi}{\mathrm{2}}\:{e}^{−\alpha} \:\:{d}\alpha\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left(\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\right){d}\alpha \\ $$$$ \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \left(\:\int_{\mathrm{0}} ^{\mathrm{1}} {cos}\left(\alpha{x}\right){d}\alpha\right)\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\left({by}\:{fubini}\:{theorem}\:\right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\:\left[\frac{{sin}\left(\alpha{x}\right)}{{x}}\:\right]_{\alpha=\mathrm{0}} ^{\alpha=\mathrm{1}} \right)\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{sinx}}{{x}}.\frac{\:{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sinx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}=\:\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\:\frac{\mathrm{1}}{{e}}\right). \\ $$$$ \\ $$
