
Question Number 27627 by Rasheed.Sindhi last updated on 11/Jan/18
Commented by Rasheed.Sindhi last updated on 11/Jan/18

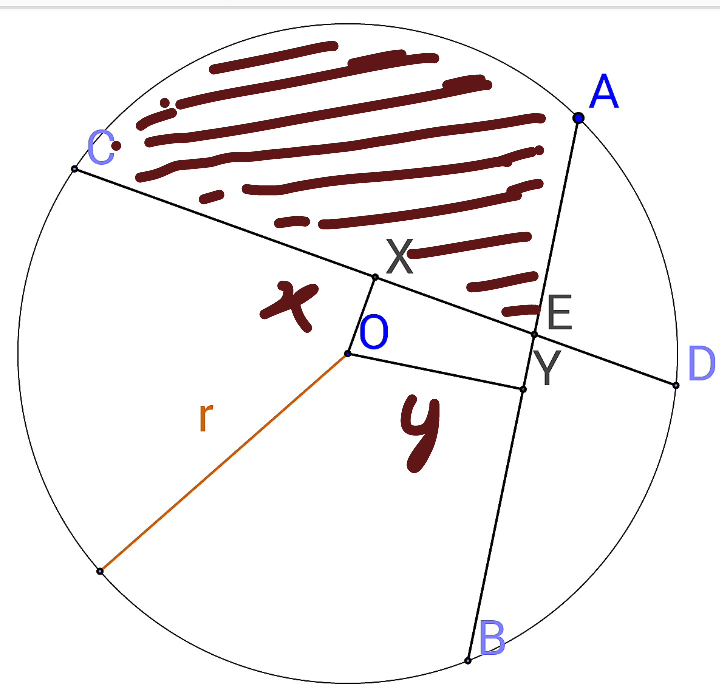
$$\mathrm{Given}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{r}.\:\mathrm{AB}\:\&\:\mathrm{CD} \\ $$$$\mathrm{are}\:\mathrm{two}\:\mathrm{chords}\:\mathrm{intersecting}\:\mathrm{at}\:\mathrm{E} \\ $$$$\mathrm{OX}\:\mathrm{and}\:\mathrm{OY}\:\mathrm{are}\:\mathrm{respective}\:\mathrm{distances} \\ $$$$\mathrm{of}\:\mathrm{chords}\:\mathrm{CD}\:\mathrm{and}\:\mathrm{AB}\:\:\mathrm{from}\:\mathrm{center} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{circle}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{region}\:\mathrm{AEC} \\ $$$$\left(\mathrm{The}\:\mathrm{region}\:\mathrm{bound}\:\mathrm{by}\:\mathrm{line}\:\mathrm{segments}\right. \\ $$$$\left.\mathrm{AE},\mathrm{CE}\:\mathrm{and}\:\mathrm{the}\:\mathrm{minor}\:\mathrm{arc}\:\overset{\frown} {\mathrm{AC}}\right)\mathrm{when} \\ $$$$\mathrm{OX}=\mathrm{x}\:,\mathrm{OY}=\mathrm{y}\: \\ $$$$\angle\mathrm{XOY}=\theta \\ $$
Answered by mrW2 last updated on 14/Jan/18

Commented by mrW2 last updated on 14/Jan/18
![Eqn. of circle: x^2 +y^2 =r^2 ⇒y=(√(r^2 −x^2 )) Eqn. of CD: y=p+kx with k=−(1/(tan θ)) CD passes through F, b sin θ=p−(1/(tan θ))×b cos θ ⇒p=b(sin θ+((cos^2 θ)/(sin θ)))=(b/(sin θ)) ⇒y=(b/(sin θ))−(1/(tan θ))x=((b−x cos θ)/(sin θ)) Point D(x_D ,y_D ): y=y_D =(√(r^2 −x^2 ))=((b−x cos θ)/(sin θ)) sin^2 θ(r^2 −x^2 )=b^2 −2b cos θ x+cos^2 θ x^2 ) x^2 −2b cos θ x−(r^2 sin^2 θ−b^2 )=0 ⇒x=x_D =((2b cos θ−(√(4b^4 cos^2 θ+4(r^2 sin^2 θ−b^2 ))))/2) ⇒x_D =b[cos θ−sin θ(√(((r/b))^2 −1))] x_C =b[cos θ+sin θ(√(((r/b))^2 −1))]≥a (!) Area A=∫_x_D ^( a) ((√(r^2 −x^2 ))−(b/(sin θ))+(1/(tan θ))x)dx =[(r^2 /2) sin^(−1) (x/r)+((x(√(r^2 −x^2 )))/2)−((bx)/(sin θ))+(x^2 /(2tan θ))]_x_D ^a ⇒A=[(r^2 /2) (sin^(−1) (a/r)−sin^(−1) (x_D /r))+((a(√(r^2 −a^2 ))−x_D (√(r^2 −x_D ^2 )))/2)−((b(a−x_D ))/(sin θ))+((a^2 −x_D ^2 )/(2tan θ))]](Q27744.png)
$${Eqn}.\:{of}\:{circle}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow{y}=\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$ \\ $$$${Eqn}.\:{of}\:{CD}: \\ $$$${y}={p}+{kx}\:{with}\:{k}=−\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$${CD}\:{passes}\:{through}\:{F}, \\ $$$${b}\:\mathrm{sin}\:\theta={p}−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}×{b}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow{p}={b}\left(\mathrm{sin}\:\theta+\frac{\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{sin}\:\theta}\right)=\frac{{b}}{\mathrm{sin}\:\theta} \\ $$$$\Rightarrow{y}=\frac{{b}}{\mathrm{sin}\:\theta}−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}{x}=\frac{{b}−{x}\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta} \\ $$$$ \\ $$$${Point}\:{D}\left({x}_{{D}} ,{y}_{{D}} \right): \\ $$$${y}={y}_{{D}} =\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\frac{{b}−{x}\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta} \\ $$$$\left.\mathrm{sin}^{\mathrm{2}} \:\theta\left({r}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)={b}^{\mathrm{2}} −\mathrm{2}{b}\:\mathrm{cos}\:\theta\:{x}+\mathrm{cos}^{\mathrm{2}} \:\theta\:{x}^{\mathrm{2}} \right) \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{b}\:\mathrm{cos}\:\theta\:{x}−\left({r}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−{b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{x}={x}_{{D}} =\frac{\mathrm{2}{b}\:\mathrm{cos}\:\theta−\sqrt{\mathrm{4}{b}^{\mathrm{4}} \:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{4}\left({r}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−{b}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{D}} ={b}\left[\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\sqrt{\left(\frac{{r}}{{b}}\right)^{\mathrm{2}} −\mathrm{1}}\right] \\ $$$$ \\ $$$${x}_{{C}} ={b}\left[\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\sqrt{\left(\frac{{r}}{{b}}\right)^{\mathrm{2}} −\mathrm{1}}\right]\geqslant{a}\:\left(!\right) \\ $$$$ \\ $$$${Area}\:{A}=\int_{{x}_{{D}} } ^{\:{a}} \left(\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }−\frac{{b}}{\mathrm{sin}\:\theta}+\frac{\mathrm{1}}{\mathrm{tan}\:\theta}{x}\right){dx} \\ $$$$=\left[\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{{r}}+\frac{{x}\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{\mathrm{2}}−\frac{{bx}}{\mathrm{sin}\:\theta}+\frac{{x}^{\mathrm{2}} }{\mathrm{2tan}\:\theta}\right]_{{x}_{{D}} } ^{{a}} \\ $$$$\Rightarrow{A}=\left[\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\:\left(\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{{r}}−\mathrm{sin}^{−\mathrm{1}} \frac{{x}_{{D}} }{{r}}\right)+\frac{{a}\sqrt{{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }−{x}_{{D}} \sqrt{{r}^{\mathrm{2}} −{x}_{{D}} ^{\mathrm{2}} }}{\mathrm{2}}−\frac{{b}\left({a}−{x}_{{D}} \right)}{\mathrm{sin}\:\theta}+\frac{{a}^{\mathrm{2}} −{x}_{{D}} ^{\mathrm{2}} }{\mathrm{2tan}\:\theta}\right] \\ $$
Commented by Rasheed.Sindhi last updated on 14/Jan/18

$$\Game\mathrm{r}\exists\forall+\:\:\:\mathbb{S}\mathrm{ir}!\: \\ $$$$\:\:\underset{\mathcal{SSS}..\mathcal{S}} {\mathrm{Than}\Bbbk}\:\vee\mathrm{ery}\:\mathrm{m}\Cup\Subset\nparallel! \\ $$$$\mathrm{Could}\:\mathrm{you}\:\mathrm{do}\:\mathrm{also}\:\mathrm{using}\:\mathrm{non}- \\ $$$$\mathrm{analytic}\:\mathrm{approach}. \\ $$
