Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 2815 by prakash jain last updated on 28/Nov/15

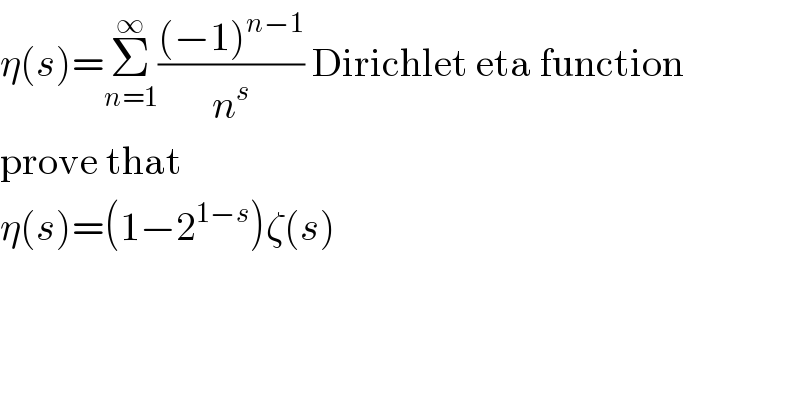
η(s)=Σ_(n=1) ^∞ (((−1)^(n−1) )/n^s ) Dirichlet eta function prove that η(s)=(1−2^(1−s) )ζ(s)

$$\eta\left({s}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{{s}} }\:\mathrm{Dirichlet}\:\mathrm{eta}\:\mathrm{function} \\ $$$$\mathrm{prove}\:\mathrm{that} \\ $$$$\eta\left({s}\right)=\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{s}} \right)\zeta\left({s}\right) \\ $$

Commented by prakash jain last updated on 27/Nov/15

This result is used in answer to Q2796.

$$\mathrm{This}\:\mathrm{result}\:\mathrm{is}\:\mathrm{used}\:\mathrm{in}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{Q2796}. \\ $$

Commented by 123456 last updated on 28/Nov/15

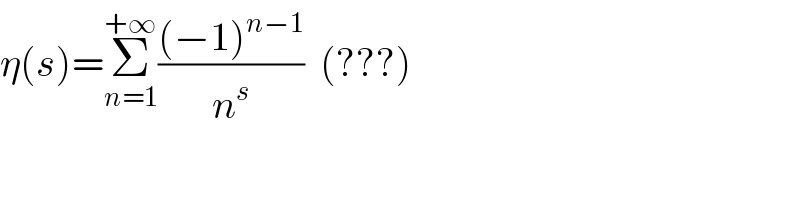
η(s)=Σ_(n=1) ^(+∞) (((−1)^(n−1) )/n^s ) (???)

$$\eta\left({s}\right)=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{{s}} }\:\:\left(???\right) \\ $$

Commented by prakash jain last updated on 28/Nov/15

Yes. corrected.

$$\mathrm{Yes}.\:\mathrm{corrected}. \\ $$

Answered by prakash jain last updated on 28/Nov/15

For s∈R, s>1 η(s)=(1/1^s )−(1/2^s )+(1/3^s )−(1/4^s )+.. η(s)=(1/1^s )+((1/2^s )−(2/2^s ))+(1/3^s )+((1/4^s )−(2/4^s ))+... taking all −ve terms towards end. series rearrangement is valid for s>1. η(s)=ζ(s)−(2/2^s )[(1/1^s )+(1/2^s )+...] η(s)=ζ(s)−2^(1−s) ζ(s) η(s)=ζ(s)(1−2^(1−s) )

$$\mathrm{For}\:{s}\in\mathbb{R},\:{s}>\mathrm{1} \\ $$$$\eta\left({s}\right)=\frac{\mathrm{1}}{\mathrm{1}^{{s}} }−\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }−\frac{\mathrm{1}}{\mathrm{4}^{{s}} }+.. \\ $$$$\eta\left({s}\right)=\frac{\mathrm{1}}{\mathrm{1}^{{s}} }+\left(\frac{\mathrm{1}}{\mathrm{2}^{{s}} }−\frac{\mathrm{2}}{\mathrm{2}^{{s}} }\right)+\frac{\mathrm{1}}{\mathrm{3}^{{s}} }+\left(\frac{\mathrm{1}}{\mathrm{4}^{{s}} }−\frac{\mathrm{2}}{\mathrm{4}^{{s}} }\right)+... \\ $$$${taking}\:{all}\:−{ve}\:{terms}\:{towards}\:{end}. \\ $$$${series}\:{rearrangement}\:{is}\:{valid}\:{for}\:{s}>\mathrm{1}. \\ $$$$\eta\left({s}\right)=\zeta\left({s}\right)−\frac{\mathrm{2}}{\mathrm{2}^{{s}} }\left[\frac{\mathrm{1}}{\mathrm{1}^{{s}} }+\frac{\mathrm{1}}{\mathrm{2}^{{s}} }+...\right] \\ $$$$\eta\left({s}\right)=\zeta\left({s}\right)−\mathrm{2}^{\mathrm{1}−{s}} \zeta\left({s}\right) \\ $$$$\eta\left({s}\right)=\zeta\left({s}\right)\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{s}} \right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com