
Question Number 28611 by abdo imad last updated on 27/Jan/18
![let give θ∈]0,π[ prove that ∫_0 ^1 (dt/(e^(−iθ) −t))= Σ_(n=1) ^(+∞) (e^(inθ) /n) .](Q28611.png)
$$\left.{let}\:{give}\:\theta\in\right]\mathrm{0},\pi\left[\:\:{prove}\:{that}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{e}^{−{i}\theta} −{t}}=\:\sum_{{n}=\mathrm{1}} ^{+\infty} \:\:\frac{{e}^{{in}\theta} }{{n}}\:\:.\right. \\ $$
Commented by abdo imad last updated on 28/Jan/18
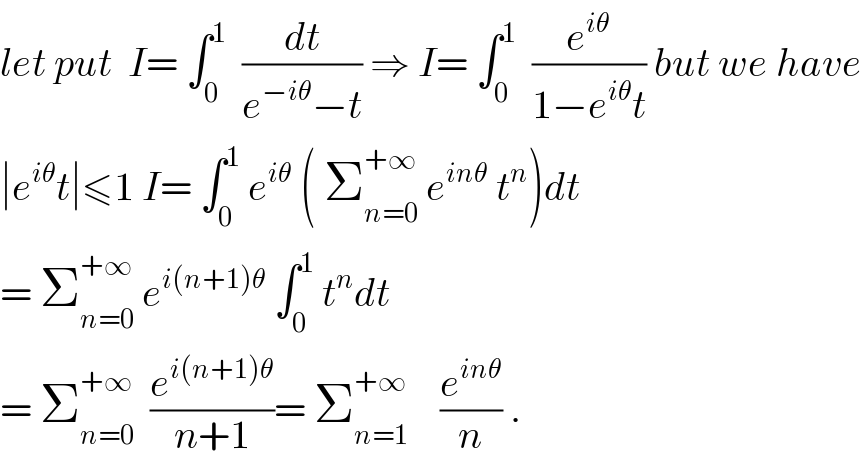
$${let}\:{put}\:\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{{e}^{−{i}\theta} −{t}}\:\Rightarrow\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{e}^{{i}\theta} }{\mathrm{1}−{e}^{{i}\theta} {t}}\:{but}\:{we}\:{have} \\ $$$$\mid{e}^{{i}\theta} {t}\mid\leqslant\mathrm{1}\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{i}\theta} \:\left(\:\sum_{{n}=\mathrm{0}} ^{+\infty} \:{e}^{{in}\theta} \:{t}^{{n}} \right){dt} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{+\infty} \:{e}^{{i}\left({n}+\mathrm{1}\right)\theta} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{n}} {dt} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{+\infty} \:\:\frac{{e}^{{i}\left({n}+\mathrm{1}\right)\theta} }{{n}+\mathrm{1}}=\:\sum_{{n}=\mathrm{1}} ^{+\infty} \:\:\:\:\frac{{e}^{{in}\theta} }{{n}}\:. \\ $$
